题目内容
13. 质量分别为ma=1kg,mb=2kg的滑块a、b用质量不计的长为L=0.2m的杆连接,将整个装置放在倾角为α=30°的长木板上,现将装置无初速释放,且释放瞬间滑块b距离地面的高度为h=0.1m,整个运动过程中不考虑滑块经过衔接处损失的能量,不计一切摩擦和阻力,重力加速度g=10m/s2,则
质量分别为ma=1kg,mb=2kg的滑块a、b用质量不计的长为L=0.2m的杆连接,将整个装置放在倾角为α=30°的长木板上,现将装置无初速释放,且释放瞬间滑块b距离地面的高度为h=0.1m,整个运动过程中不考虑滑块经过衔接处损失的能量,不计一切摩擦和阻力,重力加速度g=10m/s2,则(1)两个滑块都进入水平面时的速度为多大?
(2)在整个运动的过程中,滑块b的机械能如何变化?变化了多少?
分析 (1)以两个滑块组成的系统为研究对象,由机械能守恒定律可以求出两个滑块都进入水平面时的速度.
(2)以b为研究对象,应用动能定理可以求出杆对b做的功,即b的机械能的变化量.或根据机械能的概念求解.
解答 解:(1)设地面为重力势能零点,根据机械能守恒定律得:
mag(Lsin30°+h)+mbgh=$\frac{1}{2}$(mA+mB)v2
得:v=$\sqrt{\frac{2{m}_{a}g(Lsin30°+h)+2{m}_{b}gh}{{m}_{a}+{m}_{b}}}$=$\sqrt{\frac{2×1×10×(0.2×0.5+0.1)+2×2×10×0.1}{1+2}}$=$\frac{2\sqrt{6}}{3}$m/s
即两两个滑块都进入水平面上运动时的速度大小为$\frac{2\sqrt{6}}{3}$m/s.
(2)下滑的整个过程中b机械能的增加量为:
△Eb=$\frac{1}{2}$mbv2-mbgh=$\frac{1}{2}$×2×($\frac{2\sqrt{6}}{3}$)2-2×10×0.1=$\frac{2}{3}$J
即滑块b的机械能增加了$\frac{2}{3}$J.
答:
(1)两个滑块都进入水平面时的速度为$\frac{2\sqrt{6}}{3}$m/s.
(2)滑块b的机械能增加了$\frac{2}{3}$J.
点评 本题是杆系系统,明确系统的机械能是守恒的,但单个物体的机械能不守恒.分析清楚物体运动过程,知道两个滑块都滑到水平面上时速度相等,应用机械能守恒定律与动能定理即可正确解题.

练习册系列答案
相关题目
3.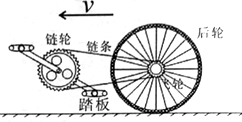 小明同学在学习了圆周运动的知识后,设计了一个通过测量脚板的转数,推算自行车的骑行速度的方法.他的设想是:测量后轮的半径R,飞轮的齿数N1,链轮的齿数N2,当测得链轮(即脚踏板)的转速为n($\frac{r}{s}$)时,可推算自行车前进速度v的表达式为( )
小明同学在学习了圆周运动的知识后,设计了一个通过测量脚板的转数,推算自行车的骑行速度的方法.他的设想是:测量后轮的半径R,飞轮的齿数N1,链轮的齿数N2,当测得链轮(即脚踏板)的转速为n($\frac{r}{s}$)时,可推算自行车前进速度v的表达式为( )
 小明同学在学习了圆周运动的知识后,设计了一个通过测量脚板的转数,推算自行车的骑行速度的方法.他的设想是:测量后轮的半径R,飞轮的齿数N1,链轮的齿数N2,当测得链轮(即脚踏板)的转速为n($\frac{r}{s}$)时,可推算自行车前进速度v的表达式为( )
小明同学在学习了圆周运动的知识后,设计了一个通过测量脚板的转数,推算自行车的骑行速度的方法.他的设想是:测量后轮的半径R,飞轮的齿数N1,链轮的齿数N2,当测得链轮(即脚踏板)的转速为n($\frac{r}{s}$)时,可推算自行车前进速度v的表达式为( )| A. | 2πn$\frac{{N}_{1}R}{{N}_{2}}$ | B. | 2πn$\frac{{N}_{2}R}{{N}_{1}}$ | C. | πn$\frac{{N}_{1}R}{{N}_{2}}$ | D. | πn$\frac{{N}_{2}}{{N}_{1}}$R |
4.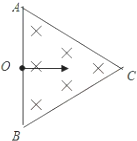 如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )
如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )
 如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )
如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )| A. | Bmin=$\frac{2m{v}_{0}}{qa}$,t=$\frac{7πa}{6v}$ | B. | Bmin=$\frac{2m{v}_{0}}{qa}$,t=$\frac{πa}{26v}$ | ||
| C. | Bmin=$\frac{6m{v}_{0}}{qa}$,t=$\frac{7πa}{6v}$ | D. | Bmin=$\frac{6m{v}_{0}}{qa}$,t=$\frac{πa}{26v}$ |
18. 德国物理学家弗兰克林和赫兹进行过气体原子激发的实验研究.如图(1)他们在一只阴极射线管中充了要考察的汞蒸气.阴极发射出的电子受阴极K和栅极R之间的电压UR加速,电子到达栅极R时,电场做功eUR.此后电子通过栅极R和阳极A之间的减速电压UA.通过阳极的电流如图(2)所示,随着加速电压增大,阳极电流在短时间内也增大.但是到达一个特定的电压值UR后.观察到电流突然减小.在这个电压值上,电子的能量刚好能够激发和它们碰撞的原子.参加碰撞的电子交出其能量,速度减小,因此到达不了阳极,阳极电流减小.eUR即为基态气体原子的激发能.得到汞原子的各个能级比基态高以下能量值:4.88eV,6.68eV,8.78eV,10.32eV(此为汞原子的电离能).若一个能量为7.97eV电子进入汞蒸气后测量它的能量可能是( )
德国物理学家弗兰克林和赫兹进行过气体原子激发的实验研究.如图(1)他们在一只阴极射线管中充了要考察的汞蒸气.阴极发射出的电子受阴极K和栅极R之间的电压UR加速,电子到达栅极R时,电场做功eUR.此后电子通过栅极R和阳极A之间的减速电压UA.通过阳极的电流如图(2)所示,随着加速电压增大,阳极电流在短时间内也增大.但是到达一个特定的电压值UR后.观察到电流突然减小.在这个电压值上,电子的能量刚好能够激发和它们碰撞的原子.参加碰撞的电子交出其能量,速度减小,因此到达不了阳极,阳极电流减小.eUR即为基态气体原子的激发能.得到汞原子的各个能级比基态高以下能量值:4.88eV,6.68eV,8.78eV,10.32eV(此为汞原子的电离能).若一个能量为7.97eV电子进入汞蒸气后测量它的能量可能是( )
 德国物理学家弗兰克林和赫兹进行过气体原子激发的实验研究.如图(1)他们在一只阴极射线管中充了要考察的汞蒸气.阴极发射出的电子受阴极K和栅极R之间的电压UR加速,电子到达栅极R时,电场做功eUR.此后电子通过栅极R和阳极A之间的减速电压UA.通过阳极的电流如图(2)所示,随着加速电压增大,阳极电流在短时间内也增大.但是到达一个特定的电压值UR后.观察到电流突然减小.在这个电压值上,电子的能量刚好能够激发和它们碰撞的原子.参加碰撞的电子交出其能量,速度减小,因此到达不了阳极,阳极电流减小.eUR即为基态气体原子的激发能.得到汞原子的各个能级比基态高以下能量值:4.88eV,6.68eV,8.78eV,10.32eV(此为汞原子的电离能).若一个能量为7.97eV电子进入汞蒸气后测量它的能量可能是( )
德国物理学家弗兰克林和赫兹进行过气体原子激发的实验研究.如图(1)他们在一只阴极射线管中充了要考察的汞蒸气.阴极发射出的电子受阴极K和栅极R之间的电压UR加速,电子到达栅极R时,电场做功eUR.此后电子通过栅极R和阳极A之间的减速电压UA.通过阳极的电流如图(2)所示,随着加速电压增大,阳极电流在短时间内也增大.但是到达一个特定的电压值UR后.观察到电流突然减小.在这个电压值上,电子的能量刚好能够激发和它们碰撞的原子.参加碰撞的电子交出其能量,速度减小,因此到达不了阳极,阳极电流减小.eUR即为基态气体原子的激发能.得到汞原子的各个能级比基态高以下能量值:4.88eV,6.68eV,8.78eV,10.32eV(此为汞原子的电离能).若一个能量为7.97eV电子进入汞蒸气后测量它的能量可能是( )| A. | 4.88eV或7.97eV | B. | 4.88eV或6.68eV | ||
| C. | 2.35eV或7.97eV | D. | 1.29eV或3.09eV或7.97eV |
6. 如图所示,虚线表示某电场中的四个等势面,相邻等势面间的电势差相等,一不计重力的带负电的粒子从右侧垂直等势面φ4向左进入电场,运动轨迹与等势面分别交于a,b,c三点,则可以判断( )
如图所示,虚线表示某电场中的四个等势面,相邻等势面间的电势差相等,一不计重力的带负电的粒子从右侧垂直等势面φ4向左进入电场,运动轨迹与等势面分别交于a,b,c三点,则可以判断( )
 如图所示,虚线表示某电场中的四个等势面,相邻等势面间的电势差相等,一不计重力的带负电的粒子从右侧垂直等势面φ4向左进入电场,运动轨迹与等势面分别交于a,b,c三点,则可以判断( )
如图所示,虚线表示某电场中的四个等势面,相邻等势面间的电势差相等,一不计重力的带负电的粒子从右侧垂直等势面φ4向左进入电场,运动轨迹与等势面分别交于a,b,c三点,则可以判断( )| A. | φ1<φ2<φ3<φ4 | |
| B. | 粒子的运动轨迹和φ3等势面也可能垂直 | |
| C. | φ4等势面上各点场强处处相等 | |
| D. | 该区域可能是点电荷和无限大金属平板形成的电场 |
3. 如图所示,弹簧振子在A、B间做简谐运动,O为平衡位置,A、B间的距离是20cm,振子由A运动到B的时间是2s,则( )
如图所示,弹簧振子在A、B间做简谐运动,O为平衡位置,A、B间的距离是20cm,振子由A运动到B的时间是2s,则( )
 如图所示,弹簧振子在A、B间做简谐运动,O为平衡位置,A、B间的距离是20cm,振子由A运动到B的时间是2s,则( )
如图所示,弹簧振子在A、B间做简谐运动,O为平衡位置,A、B间的距离是20cm,振子由A运动到B的时间是2s,则( )| A. | 从O→B→O振子做了一次全振动 | |
| B. | 振动周期为2 s,振幅是10 cm | |
| C. | 从B开始经过6 s,振子通过的路程是60 cm | |
| D. | 振子在经过C点时速度大小一定相等,加速度也一定相等 | |
| E. | 从O开始经过3 s,振子的弹性势能最大 |
 如图所示为圆形轨道的四分之三,圆轨道半径为0.5m,把它固定在水平地面在轨道最底端放置两个小球,A球质量为0.2kg,B球质量为0.4kg,中间有塑胶炸药,现把塑胶炸药引爆,两小球被推开,已知A球刚好能通过圆的最高点.(g=10m/s2)求:
如图所示为圆形轨道的四分之三,圆轨道半径为0.5m,把它固定在水平地面在轨道最底端放置两个小球,A球质量为0.2kg,B球质量为0.4kg,中间有塑胶炸药,现把塑胶炸药引爆,两小球被推开,已知A球刚好能通过圆的最高点.(g=10m/s2)求: