题目内容
3. 如图所示,在质量为m=1kg的物体O上系着两条细绳.长为30cm的细绳OA的一端连着套在水平棒上可以滑动的轻质圆环A上,环与棒间的动摩擦因数为0.75;另-条细绳跨过与圆环A在同一高度,且相距50cm的光滑定滑轮B (滑轮很小,且与水平棒的距离可忽略不计),与重物C相连接,此时圆环A刚要滑动(认为最大静摩檫力与滑动摩擦力相等).求:
如图所示,在质量为m=1kg的物体O上系着两条细绳.长为30cm的细绳OA的一端连着套在水平棒上可以滑动的轻质圆环A上,环与棒间的动摩擦因数为0.75;另-条细绳跨过与圆环A在同一高度,且相距50cm的光滑定滑轮B (滑轮很小,且与水平棒的距离可忽略不计),与重物C相连接,此时圆环A刚要滑动(认为最大静摩檫力与滑动摩擦力相等).求:(1)细绳OA的张力大小;
(2)圆环将要滑动时,重物C的质量是多少?
分析 (1)以圆环为研究对象,圆环将要开始滑动,在共点力作用下仍处于平衡状态,根据平衡条件求出θ.由几何知识求出角φ.以物体O为研究对象,根据平衡条件求出长为30cm的细绳的张力.
(2)圆环将要开始滑动时,长为30cm的细绳的张力已求出,以物体O为研究对象,由平衡条件求出重物G的质量.
解答  解:对环,如图1所示:由平衡条件?Fx=0,?Fy=0,建立方程有:
解:对环,如图1所示:由平衡条件?Fx=0,?Fy=0,建立方程有:
μFN-FTcosθ=0,
FN-FTsinθ=0.
所以tanθ=$\frac{1}{μ}$=$\frac{4}{3}$,θ=arctan$\frac{1}{μ}$=arctan$\frac{4}{3}$=53°
因AB=50cm,AO=30cm,根据数学知识得AOB是直角三角形,φ=90°.
(1)以物体O为研究对象,分析受力如图2所示,选取坐标系,根据平衡条件有:
Gcosθ+FTsinθ-mg=0
FTcosθ-Gsinθ=0.
即:FT=8N.
(2)以物体O为研究对象,环将要滑动时,得:
mGgsinθ=FTcosθ,
解得:mG=0.6kg.
答:(1)长为30cm的细绳的张力是8N.
(2)圆环将要开始滑动时,重物G的质量是0.6kg.
点评 本题涉及三个物体平衡的问题,分析受力时要注意环的重力不计.当环刚要滑动时静摩擦力达到最大值.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
11. 如图所示,粗糙的固定斜面上放置一质量为m的木箱,斜面的倾角为α=30°,木箱与斜面间的动摩擦因数为μ=$\frac{{\sqrt{3}}}{3}$,先对木箱施一拉力F,使木箱沿斜面向上做匀速直线运动.设F的方向与水平面的夹角为θ(图中未画出),在θ从0°逆时针逐渐增大到90°的过程中,木箱的速度保持不变,则( )
如图所示,粗糙的固定斜面上放置一质量为m的木箱,斜面的倾角为α=30°,木箱与斜面间的动摩擦因数为μ=$\frac{{\sqrt{3}}}{3}$,先对木箱施一拉力F,使木箱沿斜面向上做匀速直线运动.设F的方向与水平面的夹角为θ(图中未画出),在θ从0°逆时针逐渐增大到90°的过程中,木箱的速度保持不变,则( )
 如图所示,粗糙的固定斜面上放置一质量为m的木箱,斜面的倾角为α=30°,木箱与斜面间的动摩擦因数为μ=$\frac{{\sqrt{3}}}{3}$,先对木箱施一拉力F,使木箱沿斜面向上做匀速直线运动.设F的方向与水平面的夹角为θ(图中未画出),在θ从0°逆时针逐渐增大到90°的过程中,木箱的速度保持不变,则( )
如图所示,粗糙的固定斜面上放置一质量为m的木箱,斜面的倾角为α=30°,木箱与斜面间的动摩擦因数为μ=$\frac{{\sqrt{3}}}{3}$,先对木箱施一拉力F,使木箱沿斜面向上做匀速直线运动.设F的方向与水平面的夹角为θ(图中未画出),在θ从0°逆时针逐渐增大到90°的过程中,木箱的速度保持不变,则( )| A. | F一直减小 | |
| B. | F的最小值为$\frac{{\sqrt{3}}}{2}$mg | |
| C. | F先减小后增大 | |
| D. | 当θ=0°时,斜面对m的作用力为Fsina+mgcosa |
8.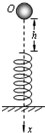 如图所示,劲度系数为k的轻弹簧竖直放置,下端固定在水平地面上,一质量为m的小球,从离弹簧上端高h处由静止释放,那么从小球压上弹簧后继续向下运动到最低点的过程中,以下说法正确的是( )
如图所示,劲度系数为k的轻弹簧竖直放置,下端固定在水平地面上,一质量为m的小球,从离弹簧上端高h处由静止释放,那么从小球压上弹簧后继续向下运动到最低点的过程中,以下说法正确的是( )
 如图所示,劲度系数为k的轻弹簧竖直放置,下端固定在水平地面上,一质量为m的小球,从离弹簧上端高h处由静止释放,那么从小球压上弹簧后继续向下运动到最低点的过程中,以下说法正确的是( )
如图所示,劲度系数为k的轻弹簧竖直放置,下端固定在水平地面上,一质量为m的小球,从离弹簧上端高h处由静止释放,那么从小球压上弹簧后继续向下运动到最低点的过程中,以下说法正确的是( )| A. | 弹簧的弹性势能逐渐增大 | |
| B. | 球刚接触弹簧时动能最大 | |
| C. | 全过程中小球的机械能守恒 | |
| D. | 该过程的某一阶段内,小球的动能增大而小球的机械能减少 |
15.“嫦娥三号”探月卫星计划于2013年下半年在西昌卫星发射中心发射,将实现“落月”的新阶段.“嫦娥三号”探月卫星到了月球附近,以速度v贴近月球表面匀速飞行,测出它的运行周期为T,已知引力常量为G,不计周围其他天体的影响,则下列说法正确的是( )
| A. | “嫦娥三号”探月卫星的轨道半径为$\frac{vT}{2π}$ | |
| B. | 月球表面的重力加速度约为$\frac{2πv}{T}$ | |
| C. | 月球的平均密度约为$\frac{3π}{G{T}^{2}}$ | |
| D. | “嫦娥三号”探月卫星的质量约为$\frac{{v}^{3}T}{2πG}$ |
 如图所示,将小砝码置于桌面上的薄纸板上,用水平向右的拉力将纸板迅速抽出,砝码的移动很小,几乎观察不到,这就是大家熟悉的惯性演示实验.若砝码和纸板的质量分别为m1和m2,各接触面间的动摩擦因数均为μ.重力加速度为g.
如图所示,将小砝码置于桌面上的薄纸板上,用水平向右的拉力将纸板迅速抽出,砝码的移动很小,几乎观察不到,这就是大家熟悉的惯性演示实验.若砝码和纸板的质量分别为m1和m2,各接触面间的动摩擦因数均为μ.重力加速度为g.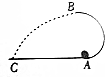 如图所示,半径为R的半圆形轨道竖直固定在水平地面上,A点是最低点,B点是最高点,质量为m的小球以5$\sqrt{gR}$的速度自A点进入半圆轨道,它经过最高点后飞出,最后落在水平地面上的C点,现测得AC=4R,重力加速度为g,不计空气阻力.求:
如图所示,半径为R的半圆形轨道竖直固定在水平地面上,A点是最低点,B点是最高点,质量为m的小球以5$\sqrt{gR}$的速度自A点进入半圆轨道,它经过最高点后飞出,最后落在水平地面上的C点,现测得AC=4R,重力加速度为g,不计空气阻力.求: