题目内容
11. 如图所示,粗糙的固定斜面上放置一质量为m的木箱,斜面的倾角为α=30°,木箱与斜面间的动摩擦因数为μ=$\frac{{\sqrt{3}}}{3}$,先对木箱施一拉力F,使木箱沿斜面向上做匀速直线运动.设F的方向与水平面的夹角为θ(图中未画出),在θ从0°逆时针逐渐增大到90°的过程中,木箱的速度保持不变,则( )
如图所示,粗糙的固定斜面上放置一质量为m的木箱,斜面的倾角为α=30°,木箱与斜面间的动摩擦因数为μ=$\frac{{\sqrt{3}}}{3}$,先对木箱施一拉力F,使木箱沿斜面向上做匀速直线运动.设F的方向与水平面的夹角为θ(图中未画出),在θ从0°逆时针逐渐增大到90°的过程中,木箱的速度保持不变,则( )| A. | F一直减小 | |
| B. | F的最小值为$\frac{{\sqrt{3}}}{2}$mg | |
| C. | F先减小后增大 | |
| D. | 当θ=0°时,斜面对m的作用力为Fsina+mgcosa |
分析 对木箱进行受力分析,根据共点力平衡,利用正交分解,在沿斜面方向和垂直于斜面方向都平衡,进行求解.
解答  解:A、对m受力分析如图1:
解:A、对m受力分析如图1:
由于摩擦力与支持力之间的关系为:f=μFN
设支持力和摩擦力的合力与支持力方向的夹角为β,不论F如何变,β均不变,则:
tanβ=$\frac{f}{{F}_{N}}=μ$
所以:β=30°
若将摩擦力和支持力的合力看作一个力,则木箱受到三个力的作用,根据三个力的作用下共点力平衡的条件可知,任意两个力的合力与第三个力一定大小相等,方向相反;在θ从0°逆时针逐渐增大到90°的过程中的受力如图2:
由图可知,当力F由水平逐渐变成竖直向上的过程中,F的大小是先减小后增大,并且根据矢量合成可知,当F的方向与支持力和摩擦力的合力的方向垂直时,F最小,由几何关系可知此时F与水平方向之间的夹角:θ=α+β=30°+30°=60°
F的大小:F=$mg•sin60°=\frac{\sqrt{3}}{2}mg$.故A错误,BC正确;
D、当θ=0°时,由平衡条件得:Fcosθ-mgsinθ-μFN=0,
FN -Fsinθ-mgcosθ=0,
解得:FN=Fsinα+mgcosα.
由于斜面对m的作用力是支持力与摩擦力的合力,故D错误.
故选:BC
点评 该图中,木箱的受力看似比较简单,但实际的分析比较复杂,解答本题的关键正确受力分析,根据共点力平衡,将支持力和摩擦力的合力作为一个力来方向,再利用正交分解进行求解,基础题.

练习册系列答案
相关题目
9.某交变电流的图象如图2所示,则该交变电流的有效值为( )
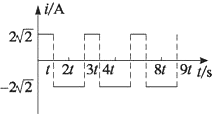

| A. | 2$\sqrt{2}$A | B. | 4 A | C. | 3.5$\sqrt{2}$A | D. | 6 A |
6.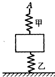 如图所示,物块质量为m,与甲、乙两弹簧相连接,乙弹簧下端与地面连接,甲、乙两弹簧质量不计,其劲度系数分别为k1、k2,起初甲弹簧处于自由长度,现用手将甲弹簧的A端缓慢上提,使乙弹簧产生的弹力大小变为原来的$\frac{2}{3}$,则A端上移距离可能是( )
如图所示,物块质量为m,与甲、乙两弹簧相连接,乙弹簧下端与地面连接,甲、乙两弹簧质量不计,其劲度系数分别为k1、k2,起初甲弹簧处于自由长度,现用手将甲弹簧的A端缓慢上提,使乙弹簧产生的弹力大小变为原来的$\frac{2}{3}$,则A端上移距离可能是( )
 如图所示,物块质量为m,与甲、乙两弹簧相连接,乙弹簧下端与地面连接,甲、乙两弹簧质量不计,其劲度系数分别为k1、k2,起初甲弹簧处于自由长度,现用手将甲弹簧的A端缓慢上提,使乙弹簧产生的弹力大小变为原来的$\frac{2}{3}$,则A端上移距离可能是( )
如图所示,物块质量为m,与甲、乙两弹簧相连接,乙弹簧下端与地面连接,甲、乙两弹簧质量不计,其劲度系数分别为k1、k2,起初甲弹簧处于自由长度,现用手将甲弹簧的A端缓慢上提,使乙弹簧产生的弹力大小变为原来的$\frac{2}{3}$,则A端上移距离可能是( )| A. | $\frac{{(k}_{1}{+k}_{2})mg}{{{3k}_{1}k}_{2}}$ | B. | $\frac{2{(k}_{1}{+k}_{2})mg}{{{3k}_{1}k}_{2}}$ | ||
| C. | $\frac{4{(k}_{1}{+k}_{2})mg}{{{3k}_{1}k}_{2}}$ | D. | $\frac{5{(k}_{1}{+k}_{2})mg}{{{3k}_{1}k}_{2}}$ |
6. 现有经过精确校准的电压表V1和V2,当分别用来测量某线路中电阻R两端a、b间的电压时,如图所示,读数分别为12.7V和12.3V,则
现有经过精确校准的电压表V1和V2,当分别用来测量某线路中电阻R两端a、b间的电压时,如图所示,读数分别为12.7V和12.3V,则
①a、b间的实际电压略大小12.7V
②a、b间的实际电压略小于12.3V
③电压表V1的内阻大于V2的内阻
④电压表V1的内阻小于V2的内阻( )
 现有经过精确校准的电压表V1和V2,当分别用来测量某线路中电阻R两端a、b间的电压时,如图所示,读数分别为12.7V和12.3V,则
现有经过精确校准的电压表V1和V2,当分别用来测量某线路中电阻R两端a、b间的电压时,如图所示,读数分别为12.7V和12.3V,则①a、b间的实际电压略大小12.7V
②a、b间的实际电压略小于12.3V
③电压表V1的内阻大于V2的内阻
④电压表V1的内阻小于V2的内阻( )
| A. | ①③ | B. | ②④ | C. | ①④ | D. | ②③ |
20.地球绕太阳和月球绕地球运行的轨道都可以近似看作是圆形的,地球和月球绕行周期之比大约是( )
| A. | 12:1 | B. | 24:1 | C. | 29:1 | D. | 30:29 |
1.质量为2kg的物体做自由落体运动,经过2s落地,g取10m/s2,关于重力做功的功率,下列说法正确的是( )
| A. | 下落过程中重力的功率是100W | B. | 下落过程中重力的功率是400W | ||
| C. | 即将落地时重力的功率是400W | D. | 即将落地时重力的功率是200W |
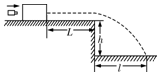 如图所示,质量为M=0.2kg的木块放在水平台面上,水平台面比水平地面高出h=0.2m,木块距水平台面的右端L=1.7m.质量为m=0.1M的子弹以v0=180m/s的速度水平射向木块,当子弹以v=90m/s的速度水平射出时,木块的速度为v1=9m/s(此过程作用时间极短,可认为木块的位移为零).若木块落到水平地面时的落地点到水平台面右端的水平距离为l=1.6m,求:(g取10m/s2)
如图所示,质量为M=0.2kg的木块放在水平台面上,水平台面比水平地面高出h=0.2m,木块距水平台面的右端L=1.7m.质量为m=0.1M的子弹以v0=180m/s的速度水平射向木块,当子弹以v=90m/s的速度水平射出时,木块的速度为v1=9m/s(此过程作用时间极短,可认为木块的位移为零).若木块落到水平地面时的落地点到水平台面右端的水平距离为l=1.6m,求:(g取10m/s2) 如图所示,在质量为m=1kg的物体O上系着两条细绳.长为30cm的细绳OA的一端连着套在水平棒上可以滑动的轻质圆环A上,环与棒间的动摩擦因数为0.75;另-条细绳跨过与圆环A在同一高度,且相距50cm的光滑定滑轮B (滑轮很小,且与水平棒的距离可忽略不计),与重物C相连接,此时圆环A刚要滑动(认为最大静摩檫力与滑动摩擦力相等).求:
如图所示,在质量为m=1kg的物体O上系着两条细绳.长为30cm的细绳OA的一端连着套在水平棒上可以滑动的轻质圆环A上,环与棒间的动摩擦因数为0.75;另-条细绳跨过与圆环A在同一高度,且相距50cm的光滑定滑轮B (滑轮很小,且与水平棒的距离可忽略不计),与重物C相连接,此时圆环A刚要滑动(认为最大静摩檫力与滑动摩擦力相等).求: