题目内容
12.已知地球半径为R,地球表面重力加速度为g.(1)不考虑地球自转的影响,取R=6400km,g=10m/s2,π=3.14,估算近地卫星绕地球做匀速圆周运动的周期T;
(2)若地球自转周期为T0,推导地球同步卫星运行轨道离地面高度h的表达式.
分析 (1)依据重力提供向心力,结合线速度与周期的关系,即可求解;
(2)根据引力提供向心力,结合黄金代换公式,即可求解.
解答 解:(1)近地卫星重力提供向心力:$mg=m\frac{v^2}{R}$
根据速度与周期的关系得:$v=\frac{2πR}{T}$
解得:$T=2π\sqrt{\frac{R}{g}}=5024$s
(2)设同步卫星的质量为m′,地球的质量为M,万有引力提供向心力,有:$G\frac{Mm'}{{{{(R+h)}^2}}}=m'{(\frac{2π}{{{T_0}^{\;}}})^2}(R+h)$
质量为m的物体,在地面附近的万有引力近似等于重力,有:$G\frac{Mm}{R^2}=mg$
故同步卫星的高度 为:$h=\root{3}{{\frac{{g{R^2}{T_0}^2}}{{4{π^2}}}}}-R$
答:(1)近地卫星绕地球做匀速圆周运动的周期5024s;
(2)地球同步卫星运行轨道离地面高度h的表达式$\root{3}{\frac{g{R}^{2}{T}_{0}^{2}}{4{π}^{2}}}-R$.
点评 考查引力与向心力表达式,掌握牛顿第二定律的内容,理解黄金代换公式的作用,同时注意符号的正确运算.

练习册系列答案
相关题目
9.某交变电流的图象如图2所示,则该交变电流的有效值为( )
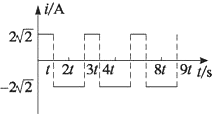

| A. | 2$\sqrt{2}$A | B. | 4 A | C. | 3.5$\sqrt{2}$A | D. | 6 A |
20.地球绕太阳和月球绕地球运行的轨道都可以近似看作是圆形的,地球和月球绕行周期之比大约是( )
| A. | 12:1 | B. | 24:1 | C. | 29:1 | D. | 30:29 |
1.质量为2kg的物体做自由落体运动,经过2s落地,g取10m/s2,关于重力做功的功率,下列说法正确的是( )
| A. | 下落过程中重力的功率是100W | B. | 下落过程中重力的功率是400W | ||
| C. | 即将落地时重力的功率是400W | D. | 即将落地时重力的功率是200W |
2. 把质量为m的小球放在竖立的弹簧上,并把小球往下按至A位置,如图甲所示;迅速松手后,弹簧把小球弹起,球升至最高位置C,如图丙所示;途中经过位置B时弹簧正好处于自由状态,如图乙所示.已知B、A的高度差为h1,C、B的高度差为h2,弹簧的质量和空气阻力均忽略不计,重力加速度为g.以下说法正确的是( )
把质量为m的小球放在竖立的弹簧上,并把小球往下按至A位置,如图甲所示;迅速松手后,弹簧把小球弹起,球升至最高位置C,如图丙所示;途中经过位置B时弹簧正好处于自由状态,如图乙所示.已知B、A的高度差为h1,C、B的高度差为h2,弹簧的质量和空气阻力均忽略不计,重力加速度为g.以下说法正确的是( )
 把质量为m的小球放在竖立的弹簧上,并把小球往下按至A位置,如图甲所示;迅速松手后,弹簧把小球弹起,球升至最高位置C,如图丙所示;途中经过位置B时弹簧正好处于自由状态,如图乙所示.已知B、A的高度差为h1,C、B的高度差为h2,弹簧的质量和空气阻力均忽略不计,重力加速度为g.以下说法正确的是( )
把质量为m的小球放在竖立的弹簧上,并把小球往下按至A位置,如图甲所示;迅速松手后,弹簧把小球弹起,球升至最高位置C,如图丙所示;途中经过位置B时弹簧正好处于自由状态,如图乙所示.已知B、A的高度差为h1,C、B的高度差为h2,弹簧的质量和空气阻力均忽略不计,重力加速度为g.以下说法正确的是( )| A. | 图甲状态时弹簧的弹性势能为mgh1 | |
| B. | 图甲状态时弹簧的弹性势能为mgh1+mgh2 | |
| C. | 从A运动到B的过程中,小球的动能先增大后减小 | |
| D. | 从A运动经过B到达C的过程中,小球机械能守恒 |
 如图所示,在质量为m=1kg的物体O上系着两条细绳.长为30cm的细绳OA的一端连着套在水平棒上可以滑动的轻质圆环A上,环与棒间的动摩擦因数为0.75;另-条细绳跨过与圆环A在同一高度,且相距50cm的光滑定滑轮B (滑轮很小,且与水平棒的距离可忽略不计),与重物C相连接,此时圆环A刚要滑动(认为最大静摩檫力与滑动摩擦力相等).求:
如图所示,在质量为m=1kg的物体O上系着两条细绳.长为30cm的细绳OA的一端连着套在水平棒上可以滑动的轻质圆环A上,环与棒间的动摩擦因数为0.75;另-条细绳跨过与圆环A在同一高度,且相距50cm的光滑定滑轮B (滑轮很小,且与水平棒的距离可忽略不计),与重物C相连接,此时圆环A刚要滑动(认为最大静摩檫力与滑动摩擦力相等).求:



 如图所示,两根固定的光滑硬杆OA与OB,夹角为θ,各套轻环C,D且C,D用细绳相连,现用一恒力F沿OB方向拉环C,当两环平衡时,绳子的拉力是$\frac{F}{sinθ}$.
如图所示,两根固定的光滑硬杆OA与OB,夹角为θ,各套轻环C,D且C,D用细绳相连,现用一恒力F沿OB方向拉环C,当两环平衡时,绳子的拉力是$\frac{F}{sinθ}$. 如图所示,质量分别为6kg和10kg的物体A、B,用轻绳连接跨在一定滑轮两侧,轻绳正好拉直,且A物体底面接触地面,B物体距地面0.8m,求:
如图所示,质量分别为6kg和10kg的物体A、B,用轻绳连接跨在一定滑轮两侧,轻绳正好拉直,且A物体底面接触地面,B物体距地面0.8m,求: