题目内容
6. 2017年4月20日19时41分,“天舟一号”货运飞船在海南文昌发射成功,在随后几天内,“天舟一号”与七个月前发射的“天宫二号”空间实验室进行了三次交会对接.对接后的轨道高度与“天宫二号”原轨道高度相同.已知万有引力常量为地球半径为R,对接前“天宫二号”的轨道半径为r、运行周期为T,根据以上信息,以 下判断正确的是( )
2017年4月20日19时41分,“天舟一号”货运飞船在海南文昌发射成功,在随后几天内,“天舟一号”与七个月前发射的“天宫二号”空间实验室进行了三次交会对接.对接后的轨道高度与“天宫二号”原轨道高度相同.已知万有引力常量为地球半径为R,对接前“天宫二号”的轨道半径为r、运行周期为T,根据以上信息,以 下判断正确的是( )| A. | 地球的质量为$\frac{4{π}^{2}{r}^{2}}{G{T}^{2}}$ | |
| B. | 地球的第一宇宙速度为$\frac{2π}{T}$$\sqrt{\frac{{r}^{3}}{R}}$ | |
| C. | 对接前,“天宫二号”的运行速度为$\frac{2πR}{T}$ | |
| D. | 对接后,“天舟一号”与“天宫二号“组合体的运行周期大于T |
分析 根据万有引力提供向心力即可求解地球的质量;地球的第一宇宙速度即近地卫星的运行速度,根据万有引力提供向心力求解;天宫二号对接前的线速度$v=\frac{2πr}{T}$;运行周期只取决于半径
解答 解:A、对接前“天宫二号”的轨道半径为r,运行周期为T,根据万有引力提供向心力,有$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$,得地球质量为M=$\frac{4{π}_{\;}^{2}{r}_{\;}^{3}}{G{T}_{\;}^{2}}$,故A错误;
B、地球的第一宇宙速度即地球的近地卫星的运行速度,根据万有引力提供向心力,有$G\frac{Mm}{{R}_{\;}^{2}}=m\frac{{v}_{1}^{2}}{R}$,得${v}_{1}^{\;}=\sqrt{\frac{GM}{R}}$=$\frac{2π}{R}\sqrt{\frac{{r}_{\;}^{3}}{R}}$,故B正确;
C、对接前,“天宫二号”的运行速度为$\frac{2πr}{T}$,故C错误;
D、因为对接后的轨道高度与“天宫二号”原轨道高度相同,因此组合体的运行周期等于T,故D错误;
故选:B
点评 本题考查了万有引力和圆周运动的表达式,根据万有引力等于向心力可以求解中心天体的质量,要理解第一宇宙速度的意义.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
15.如图所示,甲图是某人站在力传感器上做下蹲-起跳动作的示意图,甲图中的“●”表示人的重心,乙图是根据力传感器画出的压力F随时间t变化的图线.乙图中a、d、f、g各点数据分别与甲图中人的a、d、f、g状态相对应,其余点对应状态没有在甲图中画出.乙图中a、c、e、i点对应的纵坐标均为610N.请根据这两个图所给出的信息,判断下列说法中正确的是( )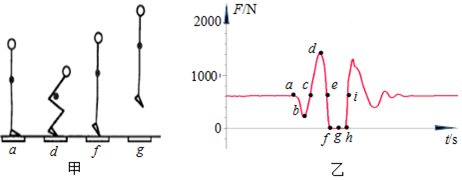

| A. | 乙图中b点时刻,人处于超重状态 | B. | 乙图中d点时刻,人处于失重状态 | ||
| C. | 乙图中g点时刻,人处于失重状态 | D. | 乙图中i点时刻,人的速度为零 |
14. 如图,质量为m的小球从斜轨道高h处由静止滑下,然后沿竖直圆轨道的内侧运动,已知圆轨道的半径为R,不计一切摩擦阻力,重力加速度为g,则下列说法正确的是( )
如图,质量为m的小球从斜轨道高h处由静止滑下,然后沿竖直圆轨道的内侧运动,已知圆轨道的半径为R,不计一切摩擦阻力,重力加速度为g,则下列说法正确的是( )
 如图,质量为m的小球从斜轨道高h处由静止滑下,然后沿竖直圆轨道的内侧运动,已知圆轨道的半径为R,不计一切摩擦阻力,重力加速度为g,则下列说法正确的是( )
如图,质量为m的小球从斜轨道高h处由静止滑下,然后沿竖直圆轨道的内侧运动,已知圆轨道的半径为R,不计一切摩擦阻力,重力加速度为g,则下列说法正确的是( )| A. | 当h≤R时,小球在运动过程中不会脱离轨道 | |
| B. | 当h=R时,小球在最低点N时对轨道压力为2mg | |
| C. | 当h=2R时,小球恰好能到达最高点M | |
| D. | 当h=2R时,小球在圆心等高处P时对轨道压力为2mg |
1.用起重机将一个质量为m的货物竖直向上以加速度a匀加速提升H米,在这个过程中,以下说法中正确的是( )
| A. | 物体的重力势能增加了maH | B. | 机械能增加了m(g+a)H | ||
| C. | 物体的动能增加了maH | D. | 物体的机械能增加了mgH |
11. 如图,在“勇敢向前冲”游戏中,挑战者要通过匀速转动的水平转盘从平台1转移到平台2上,假设挑战者成功跳到转盘上时都能立即与转盘保持相对静止,则挑战者在转盘上距转轴较近的落点A与转盘边缘上的点B一定具有相同的( )
如图,在“勇敢向前冲”游戏中,挑战者要通过匀速转动的水平转盘从平台1转移到平台2上,假设挑战者成功跳到转盘上时都能立即与转盘保持相对静止,则挑战者在转盘上距转轴较近的落点A与转盘边缘上的点B一定具有相同的( )
 如图,在“勇敢向前冲”游戏中,挑战者要通过匀速转动的水平转盘从平台1转移到平台2上,假设挑战者成功跳到转盘上时都能立即与转盘保持相对静止,则挑战者在转盘上距转轴较近的落点A与转盘边缘上的点B一定具有相同的( )
如图,在“勇敢向前冲”游戏中,挑战者要通过匀速转动的水平转盘从平台1转移到平台2上,假设挑战者成功跳到转盘上时都能立即与转盘保持相对静止,则挑战者在转盘上距转轴较近的落点A与转盘边缘上的点B一定具有相同的( )| A. | 转动半径 | B. | 线速度 | C. | 角速度 | D. | 向心加速度 |
18.一个物体从地面竖直上抛,到达最高点后又落回抛出点,若上升和下降过程中物体所受空气阻力大小恒定,则( )
| A. | 物体下落过程的加速度大于上升过程的加速度 | |
| B. | 物体下落过程所用的时间大于上升过程所用的时间 | |
| C. | 物体下落过程中的平均速度大于上升过程中的平均速度 | |
| D. | 物体下落到抛出点的速率与抛出时的速率相等 |
15.有一宇宙飞船,它的正前方横截面面积为S,以速度υ飞人宇宙微粒尘区,尘区每1m3空间有n个微粒,每一微粒平均质量设为m,设微粒尘与飞船碰撞后全部附着于飞船 上,若要使飞船的速度保持不变,则关于下列说法中正确的是( )
| A. | 牵引力增量应为:△F=nmsυ2 | |
| B. | 牵引力增量应为:△F=$\frac{1}{2}$nmsυ2 | |
| C. | 发动机功率增加量应为:△P=nmsυ3 | |
| D. | 发动机功率增加量应为:△P=$\frac{1}{2}$nmsυ3 |
 在如图所示的皮带传动装置中,a是小轮边缘上的一点,b是大轮边缘上的一点,两轮半径之比为2:3.当皮带轮匀速转动时,皮带与轮间不打滑.a、b两点的线速度之比为1:1,a、b两点的角速度之比为3:2.
在如图所示的皮带传动装置中,a是小轮边缘上的一点,b是大轮边缘上的一点,两轮半径之比为2:3.当皮带轮匀速转动时,皮带与轮间不打滑.a、b两点的线速度之比为1:1,a、b两点的角速度之比为3:2. 如图所示,从位于水面下方300m深处的A点,向水面持续发出两束频率不同的激光a、b,当入射角都为45°时,激光a恰好无法透出水面,激光b从发出至到达水面的时间为$\sqrt{3}$×10-6s,b从水面射出后,在岸边的陡壁上距水面高为100$\sqrt{3}$处留下光点B.已知光在水面上方空气中的传播速度为3×108m/s,求:
如图所示,从位于水面下方300m深处的A点,向水面持续发出两束频率不同的激光a、b,当入射角都为45°时,激光a恰好无法透出水面,激光b从发出至到达水面的时间为$\sqrt{3}$×10-6s,b从水面射出后,在岸边的陡壁上距水面高为100$\sqrt{3}$处留下光点B.已知光在水面上方空气中的传播速度为3×108m/s,求: