题目内容
12. 如图所示,相距为d的两条水平虚线之间是方向水平向里的匀强磁场,磁感应强度为B,正方形线圈abcd边长为L(L<d),质量为m、电阻为R,现将线圈在磁场上方h高处由静止释放,cd边刚进入磁场时速度为v0,cd边刚离开磁场时速度也为v0,则线圈穿过磁场的过程中(从cd边刚进入磁场起一直到ab边离开磁场为止),下列说法正确的是( )
如图所示,相距为d的两条水平虚线之间是方向水平向里的匀强磁场,磁感应强度为B,正方形线圈abcd边长为L(L<d),质量为m、电阻为R,现将线圈在磁场上方h高处由静止释放,cd边刚进入磁场时速度为v0,cd边刚离开磁场时速度也为v0,则线圈穿过磁场的过程中(从cd边刚进入磁场起一直到ab边离开磁场为止),下列说法正确的是( )| A. | 感应电流所做的功为mgd | |
| B. | 感应电流所做的功为mg(d-L) | |
| C. | 当线圈的ab边刚进入磁场时速度最小 | |
| D. | 线圈的最小速度可能为$\frac{mgR}{{B}^{2}{L}^{2}}$ |
分析 线圈下边cd刚进入磁场和刚穿出磁场时刻的速度是相同的,动能不变,根据动能定理求解感应电流做功.
线圈全部进入磁场不受安培力,要做匀加速运动,线圈进入磁场必定要做减速运动,研究线框完全在磁场中运动的过程,由平衡条件求最小速度.
解答 解:AB、从cd边刚进入磁场起一直到ab边离开磁场过程中,根据动能定理可得:mg(d+L)+WA=0,所以WA=-mg(d+L).故AB错误.
C、由于cd边刚进入磁场时速度为v0,cd边刚离开磁场时速度也为v0,所以线框进入磁场过程中可能先做减速运动,在完全进入磁场前已做匀速运动,此种情况下线圈完全进入磁场前速度已经最小;
线圈进入磁场也可能一直减速运动,完全进入磁场后做加速运动,离开磁场的情况与进入磁场情况相同,所以当线圈的ab边刚进入磁场时或刚离开磁场时速度最小.故C错误.
D、线框可能先做减速运动,在完全进入磁场前已做匀速运动,刚完全进入磁场时的速度最小,则 mg=BIL=$\frac{{B}^{2}{L}^{2}v}{R}$,则最小速度可能为 v=$\frac{mgR}{{B}^{2}{L}^{2}}$.故D正确.
故选:D.
点评 解决本题的关键根据根据线圈cd边刚进入磁场和刚穿出磁场时刻的速度都是v0,且全部进入磁场将做加速运动,判断出线圈进磁场后先做变减速运动,也得出全部进磁场时的速度是穿越磁场过程中的最小速度.

练习册系列答案
相关题目
15. 如图所示,“Verriickt”是世界上最高、最长的滑水道,游客乘坐皮艇从a点由静止沿滑水道滑下,滑到最低点b后冲上弧形轨道(c为最高点),最后到达终点,在营运前的安全测试中,测试假人有被抛出滑道的现象,下列分析正确的是( )
如图所示,“Verriickt”是世界上最高、最长的滑水道,游客乘坐皮艇从a点由静止沿滑水道滑下,滑到最低点b后冲上弧形轨道(c为最高点),最后到达终点,在营运前的安全测试中,测试假人有被抛出滑道的现象,下列分析正确的是( )
 如图所示,“Verriickt”是世界上最高、最长的滑水道,游客乘坐皮艇从a点由静止沿滑水道滑下,滑到最低点b后冲上弧形轨道(c为最高点),最后到达终点,在营运前的安全测试中,测试假人有被抛出滑道的现象,下列分析正确的是( )
如图所示,“Verriickt”是世界上最高、最长的滑水道,游客乘坐皮艇从a点由静止沿滑水道滑下,滑到最低点b后冲上弧形轨道(c为最高点),最后到达终点,在营运前的安全测试中,测试假人有被抛出滑道的现象,下列分析正确的是( )| A. | 假人经过c点时处于超重状态 | B. | 假人在弧形轨道上做匀速圆周运动 | ||
| C. | 假人被抛出的位置一定是c点 | D. | 出发点a点一定比c点高 |
3. 如图所示为“研究带电粒子在匀强磁场中运动”的演示仪结构图.若励磁线圈产生的匀强磁场方向垂直纸面向外,电子束由电子枪产生,其速度方向与磁场方向垂直且水平向右,电子速度的大小ν和磁场的磁感应强度B可分别由通过电子枪的加速电压和励磁线圈的电流来调节,则下列说法正确的是( )
如图所示为“研究带电粒子在匀强磁场中运动”的演示仪结构图.若励磁线圈产生的匀强磁场方向垂直纸面向外,电子束由电子枪产生,其速度方向与磁场方向垂直且水平向右,电子速度的大小ν和磁场的磁感应强度B可分别由通过电子枪的加速电压和励磁线圈的电流来调节,则下列说法正确的是( )
 如图所示为“研究带电粒子在匀强磁场中运动”的演示仪结构图.若励磁线圈产生的匀强磁场方向垂直纸面向外,电子束由电子枪产生,其速度方向与磁场方向垂直且水平向右,电子速度的大小ν和磁场的磁感应强度B可分别由通过电子枪的加速电压和励磁线圈的电流来调节,则下列说法正确的是( )
如图所示为“研究带电粒子在匀强磁场中运动”的演示仪结构图.若励磁线圈产生的匀强磁场方向垂直纸面向外,电子束由电子枪产生,其速度方向与磁场方向垂直且水平向右,电子速度的大小ν和磁场的磁感应强度B可分别由通过电子枪的加速电压和励磁线圈的电流来调节,则下列说法正确的是( )| A. | 仅增大励磁线圈中的电流,电子束运动轨迹的半径将变大 | |
| B. | 仅提高电子枪的加速电压,电子束运动轨迹的半径将变大 | |
| C. | 仅增大励磁线圈中的电流,电子做圆周运动的周期不变 | |
| D. | 仅提高电子枪的加速电压,电子做圆周运动的周期不变 |
17.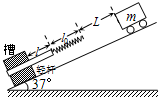 倾角为37°的光滑斜面上固定一个槽,劲度系数k=20N/m,原长l0=0.6m的轻弹簧下端与轻杆相连,开始时杆在槽外的长度l=0.3m,且杆可在槽内移动,杆与槽间的滑动摩擦力大小F1=6N,杆与槽之间的最大静摩擦力等于滑动摩擦力,质量m=1kg的小车从距弹簧上端L=0.6m处由静止释放沿斜面向下运动.已知弹性势能Ep=$\frac{1}{2}$kx2,式中x为弹簧的形变量,g=10m/s2,sin37°=0.6,关于小车和杆的运动情况,下列说法正确的是( )
倾角为37°的光滑斜面上固定一个槽,劲度系数k=20N/m,原长l0=0.6m的轻弹簧下端与轻杆相连,开始时杆在槽外的长度l=0.3m,且杆可在槽内移动,杆与槽间的滑动摩擦力大小F1=6N,杆与槽之间的最大静摩擦力等于滑动摩擦力,质量m=1kg的小车从距弹簧上端L=0.6m处由静止释放沿斜面向下运动.已知弹性势能Ep=$\frac{1}{2}$kx2,式中x为弹簧的形变量,g=10m/s2,sin37°=0.6,关于小车和杆的运动情况,下列说法正确的是( )
 倾角为37°的光滑斜面上固定一个槽,劲度系数k=20N/m,原长l0=0.6m的轻弹簧下端与轻杆相连,开始时杆在槽外的长度l=0.3m,且杆可在槽内移动,杆与槽间的滑动摩擦力大小F1=6N,杆与槽之间的最大静摩擦力等于滑动摩擦力,质量m=1kg的小车从距弹簧上端L=0.6m处由静止释放沿斜面向下运动.已知弹性势能Ep=$\frac{1}{2}$kx2,式中x为弹簧的形变量,g=10m/s2,sin37°=0.6,关于小车和杆的运动情况,下列说法正确的是( )
倾角为37°的光滑斜面上固定一个槽,劲度系数k=20N/m,原长l0=0.6m的轻弹簧下端与轻杆相连,开始时杆在槽外的长度l=0.3m,且杆可在槽内移动,杆与槽间的滑动摩擦力大小F1=6N,杆与槽之间的最大静摩擦力等于滑动摩擦力,质量m=1kg的小车从距弹簧上端L=0.6m处由静止释放沿斜面向下运动.已知弹性势能Ep=$\frac{1}{2}$kx2,式中x为弹簧的形变量,g=10m/s2,sin37°=0.6,关于小车和杆的运动情况,下列说法正确的是( )| A. | 小车先做匀加速运动,然后做加速度逐渐减小的变加速运动,最后做匀速直线运动 | |
| B. | 小车先做匀加速运动,后做加速度逐渐减小的变加速运动 | |
| C. | 杆刚要滑动时小车已通过的位移为0.9m | |
| D. | 杆从开始运动到完全进入槽内所用时间为0.1s |
4.对玻尔理论的评论和议论,正确的是( )
| A. | 玻尔理论的成功,说明经典电磁理论不适用丁原子系统,也说明了电磁理论不适用于电子运动 | |
| B. | 玻尔理论成功地解释了氢原子光谱的规律,为量子力学的建立奠定了基础 | |
| C. | 玻尔理论的成功之处是引入量子观念 | |
| D. | 玻尔理论的成功之处,是它保留了经典理论中的一些观点,如电子轨道的概念 |
 如图所示,两根足够长平行金属导轨MN、PQ固定在倾角θ=37°的绝缘斜面上,顶部接有一阻值R=1Ω的定值电阻,下端开口,轨道间距L=1m.整个装置处于磁感应强度B=4T的匀强磁场中,磁场方向垂直斜面向下.质量m=2kg的金属棒ab置于导轨上,ab在导轨之间的电阻r=1Ω,电路中其余电阻不计.金属棒ab由静止释放后沿导轨运动时始终垂直于导轨且与导轨接触良好.已知金属棒ab与导轨间动摩擦因数μ=0.5,不计空气阻力影响.sin37°=0.6,cos37°=0.8,取g=10m/s2.求:
如图所示,两根足够长平行金属导轨MN、PQ固定在倾角θ=37°的绝缘斜面上,顶部接有一阻值R=1Ω的定值电阻,下端开口,轨道间距L=1m.整个装置处于磁感应强度B=4T的匀强磁场中,磁场方向垂直斜面向下.质量m=2kg的金属棒ab置于导轨上,ab在导轨之间的电阻r=1Ω,电路中其余电阻不计.金属棒ab由静止释放后沿导轨运动时始终垂直于导轨且与导轨接触良好.已知金属棒ab与导轨间动摩擦因数μ=0.5,不计空气阻力影响.sin37°=0.6,cos37°=0.8,取g=10m/s2.求: 如图1所示,间距为L=1m、电阻不计的足够长平行光滑金属导轨水平放置,导轨左端用一阻值为R=1Ω的电阻连接,导轨上横跨一根质量为m=0.1kg、电阻也为R=1Ω的导体棒MN,导体棒与导轨接触良好,整个装置处于竖直向上、磁感应强度为B=1T的匀强磁场中.现对导体棒MN施加一水平向右的拉力F,1s时撤去拉力,导体棒继续向右滑动了一段后静止,其速度-时间图象如图2所示.已知撤去拉力前后通过电阻R的电荷量之比为1:4,重力加速度为g=10m/s2.求:
如图1所示,间距为L=1m、电阻不计的足够长平行光滑金属导轨水平放置,导轨左端用一阻值为R=1Ω的电阻连接,导轨上横跨一根质量为m=0.1kg、电阻也为R=1Ω的导体棒MN,导体棒与导轨接触良好,整个装置处于竖直向上、磁感应强度为B=1T的匀强磁场中.现对导体棒MN施加一水平向右的拉力F,1s时撤去拉力,导体棒继续向右滑动了一段后静止,其速度-时间图象如图2所示.已知撤去拉力前后通过电阻R的电荷量之比为1:4,重力加速度为g=10m/s2.求: 如右图所示,a、b是同种材料(非超导材料)制成的等长导体棒,静止于水平面内足够长的光滑水平导轨上,b的质量是a的2倍,匀强磁场垂直于纸面向里.若给a 导体棒4.5J的初动能使之向左运动,不计导轨的电阻,则整个过程中a棒产生的热量最大值为( )
如右图所示,a、b是同种材料(非超导材料)制成的等长导体棒,静止于水平面内足够长的光滑水平导轨上,b的质量是a的2倍,匀强磁场垂直于纸面向里.若给a 导体棒4.5J的初动能使之向左运动,不计导轨的电阻,则整个过程中a棒产生的热量最大值为( ) 一辆由电动机提供牵引力的实验小车在水平的直轨道上由静止开始运动,其运动的全过程转化为如图所示的v-t图象,图象显示2s-10s时间段内的图象为曲线,其余时间段图象均为直线.已知实验小车运动的过程中,2s-14s时间段内小车的功率保持不变,在14s末关闭发动机而让小车自由滑行.已知小车的质量为1kg,假设在整个运动过程中小车所受到的阻力大小不变.求:
一辆由电动机提供牵引力的实验小车在水平的直轨道上由静止开始运动,其运动的全过程转化为如图所示的v-t图象,图象显示2s-10s时间段内的图象为曲线,其余时间段图象均为直线.已知实验小车运动的过程中,2s-14s时间段内小车的功率保持不变,在14s末关闭发动机而让小车自由滑行.已知小车的质量为1kg,假设在整个运动过程中小车所受到的阻力大小不变.求: