题目内容
18. 如图所示,电子(质量m,电量e)经加速电场(电压为U1)后由中央进入偏转电场(电压为U2),然后从下极板的边缘飞出偏转电场,电子飞出电场时的动能为$({{U_1}+\frac{U_2}{2}})e$;已知偏转电场极板长度为L,板间距离为d,该电子在偏转电场运动的加速度大小是a=$\frac{{{U_2}e}}{md}$.
如图所示,电子(质量m,电量e)经加速电场(电压为U1)后由中央进入偏转电场(电压为U2),然后从下极板的边缘飞出偏转电场,电子飞出电场时的动能为$({{U_1}+\frac{U_2}{2}})e$;已知偏转电场极板长度为L,板间距离为d,该电子在偏转电场运动的加速度大小是a=$\frac{{{U_2}e}}{md}$.
分析 明确带电粒子在运动中各力做功情况,根据动能定理可求得电子的动能;再对偏转电场中受力情况分析,根据牛顿第二定律可求得加速度大小.
解答 解:由题意可知,电子在加速电场和偏转电场中电场力做功,由动能定理可知:
U1e+$\frac{{U}_{2}e}{2}$=Ek
解得:粒子飞出电场时的动能为:
EK=$({{U_1}+\frac{U_2}{2}})e$,
电子在偏转电场中只受电场力,则加速度为:
a=$\frac{F}{m}$=$\frac{{U}_{2}e}{md}$;
故答案为:$({{U_1}+\frac{U_2}{2}})e$,$\frac{{{U_2}e}}{md}$
点评 本题考查带电粒子在电场中的受力分析和功能关系的应用,要注意明确电子在偏转电场中恰好由中间位置到达下极板,则电势差为$\frac{{U}_{2}}{2}$,电场力做功为$\frac{{U}_{2}e}{2}$.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
6. 一个带电荷量为-q、质量为m的小球从光滑绝缘的斜面轨道的A点由静止下滑,小球恰能通过半径为R的竖直圆形轨道的最高点B而做圆周运动.现在竖直方向上加如图所示的匀强电场,且电场强度满足mg=2qE.若仍从A点由静止释放该小球,则( )
一个带电荷量为-q、质量为m的小球从光滑绝缘的斜面轨道的A点由静止下滑,小球恰能通过半径为R的竖直圆形轨道的最高点B而做圆周运动.现在竖直方向上加如图所示的匀强电场,且电场强度满足mg=2qE.若仍从A点由静止释放该小球,则( )
 一个带电荷量为-q、质量为m的小球从光滑绝缘的斜面轨道的A点由静止下滑,小球恰能通过半径为R的竖直圆形轨道的最高点B而做圆周运动.现在竖直方向上加如图所示的匀强电场,且电场强度满足mg=2qE.若仍从A点由静止释放该小球,则( )
一个带电荷量为-q、质量为m的小球从光滑绝缘的斜面轨道的A点由静止下滑,小球恰能通过半径为R的竖直圆形轨道的最高点B而做圆周运动.现在竖直方向上加如图所示的匀强电场,且电场强度满足mg=2qE.若仍从A点由静止释放该小球,则( )| A. | 小球仍恰好过B点 | |
| B. | 小球不能过B点 | |
| C. | 小球能过B点,且在B点与轨道之间压力不为0 | |
| D. | 以上说法都不对 |
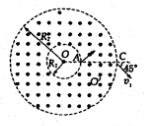 如图所示,在以O为圆心,内外半径分别为R1和R2的圆环区域内,存在垂直纸面的匀强磁场,R1=R0,R2=3R0,一电荷量为+q,质量为m的粒子从内圆上的A点进入该区域,不计重力.
如图所示,在以O为圆心,内外半径分别为R1和R2的圆环区域内,存在垂直纸面的匀强磁场,R1=R0,R2=3R0,一电荷量为+q,质量为m的粒子从内圆上的A点进入该区域,不计重力.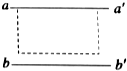 如图所示,某同学在利用插针法测定玻璃砖折射率的实验中误将界面bb′画得离开玻璃砖边缘一段距离,但自己并未察觉.则他测得的折射率将小于(填“大于”、“等于”或“小于”真实值).
如图所示,某同学在利用插针法测定玻璃砖折射率的实验中误将界面bb′画得离开玻璃砖边缘一段距离,但自己并未察觉.则他测得的折射率将小于(填“大于”、“等于”或“小于”真实值).