题目内容
3.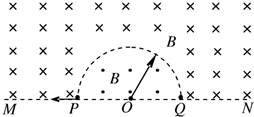 如图所示,直线MN下方无磁场,上方空间存在两个匀强磁场,其分界线是半径为R的半圆,两侧的磁场方向相反且垂直于纸面,磁感应强度大小都为B.现有一质量为m、电荷量为q的带负电微粒从P点沿半径方向向左侧射出,最终打到Q点,不计微粒的重力.求:
如图所示,直线MN下方无磁场,上方空间存在两个匀强磁场,其分界线是半径为R的半圆,两侧的磁场方向相反且垂直于纸面,磁感应强度大小都为B.现有一质量为m、电荷量为q的带负电微粒从P点沿半径方向向左侧射出,最终打到Q点,不计微粒的重力.求:(1)微粒在磁场中运动的周期;
(2)从P点到Q点,微粒的运动速度大小;
(3)若向里磁场是有界的,分布在以O点为圆心、半径为R和2R的两半圆之间的区域,上述微粒仍从P点沿半径方向向左侧射出,且微粒仍能到达Q点,求其速度的最大值.
分析 (1)带电粒子在磁场中只受洛伦兹力,粒子在磁场中做匀速圆周运动.由牛顿第二定律和圆周运动规律求出周期.
(2)根据题意作出粒子可能的运动轨迹,由牛顿第二定律与数学知识分析答题.
(3)由几何知识分析轨迹半径的最大值,由半径公式求出速度的最大值.
解答 解:(1)由qvB=m$\frac{{v}^{2}}{r}$及T=$\frac{2πr}{v}$得:
微粒在磁场中运动的周期 T=$\frac{2πm}{Bq}$.
(2)令n表示带电粒子在磁场中运动时的圆心个数,则
由几何关系可知,微粒运动的轨道半径r应满足:r=Rtan$\frac{π}{2n}$,(n=2,3,4,5,…),
结合(1)可知,v=$\frac{qBr}{m}=\frac{qB}{m}Rtan\frac{π}{2n}$,(n=2,3,4,5,…);
相应的运动轨迹所对应的圆心角φ满足:
①当n为偶数时,φ=(2π-$\frac{n-1}{n}$π)$\frac{n}{2}$+$\frac{n-1}{n}$π$•\frac{n}{2}$=nπ;(n=2,4,6,8,…)
②当n为奇数时,φ=(2π-$\frac{n-1}{n}$π)$\frac{n+1}{2}$+$\frac{n-1}{n}$π$•\frac{n-1}{2}$=$\frac{{n}^{2}+1}{n}$;(n=3,5,7,9,…)
对应的运动时间t满足:
①当n为偶数时,t=$\frac{n}{2}T=\frac{nπm}{Bq}$,(n=2,4,6,8,…);
②当n为奇数时,t=$\frac{{n}^{2}+1}{n}•\frac{T}{2}$=$\frac{({n}^{2}+1)πm}{nBq}$;(n=3,5,7,9,…)
(3)由几何关系可知,rn+$\frac{{r}_{n}}{sin\frac{π}{2n}}$≤2R,(n=2,3,4,5,…);
得:当n=3时,r可取满足条件的最大值,rmax=$\frac{\sqrt{3}}{3}R$,
相应的粒子速度vmax=$\frac{\sqrt{3}qBR}{3m}$.
相应的运动轨迹如图所示.
答:
(1)微粒在磁场中运动的周期为$\frac{2πm}{Bq}$;
(2)从P点到Q点,微粒的运动速度大小为$\frac{qB}{m}Rtan\frac{π}{2n}$,(n=2,3,4,5,…);对应的运动时间;①当n为偶数时,t=$\frac{nπm}{Bq}$,(n=2,4,6,8,…);②当n为奇数时,t=$\frac{({n}^{2}+1)πm}{nBq}$;(n=3,5,7,9,…);
(3)速度的最大值是$\frac{\sqrt{3}qBR}{3m}$.
点评 此题对运动轨迹的特殊性研究到一般性探究,这是分析问题的一种方法.同时要利用圆的特性与物理规律相结合.本题是一道难题,根据题意作出粒子的运动轨迹是本题解题的难点,也是正确解题的关键.

 如图所示,质量为m带电量为q的小球用长L的绝缘轻线系于O点,整个装置处于水平的匀强电场中.小球静止时悬线与竖直方向夹角的正切值为tanθ.若在O点放一点电荷+Q,则小球再次静止时悬线与竖直方向夹角的正切值为tanФ.下列说法正确的是( )
如图所示,质量为m带电量为q的小球用长L的绝缘轻线系于O点,整个装置处于水平的匀强电场中.小球静止时悬线与竖直方向夹角的正切值为tanθ.若在O点放一点电荷+Q,则小球再次静止时悬线与竖直方向夹角的正切值为tanФ.下列说法正确的是( )| A. | tanФ>tanθ | B. | tanФ<tanθ | C. | tanФ=tanθ | D. | 无法判断 |
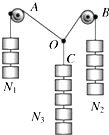 某同学利用如图所示的装置来验证力的平行四边形定则:在竖直木板上铺有白纸,固定两个光滑的滑轮A和B,将绳子打一个结点O,每个钩码的重量相等,当系统达到平衡时,根据钩码个数N的取值,可知三根绳子的拉力大小TOA、TOB和TOC,下列选项正确的是( )
某同学利用如图所示的装置来验证力的平行四边形定则:在竖直木板上铺有白纸,固定两个光滑的滑轮A和B,将绳子打一个结点O,每个钩码的重量相等,当系统达到平衡时,根据钩码个数N的取值,可知三根绳子的拉力大小TOA、TOB和TOC,下列选项正确的是( )| A. | 若N3=4,N1=1,N2=2,可以完成实验 | |
| B. | 若N2=4不变,为了完成实验,每次操作都必须使结点O在同一位置 | |
| C. | 无论在C处挂几个钩码,每次实验都必须记录OA、OB、OC三段绳子的方向和所挂钩码的个数 | |
| D. | 为了减少误差,在OA、OB两段绳子上选取相对较远的两个点来确定拉力的方向 |
| A. | 爱因斯坦的光子说解释了光电效应,光电子的最大初动能与入射光频率有关 | |
| B. | 各种原子的发光光谱都是线状谱,可将太阳光谱中的暗线与元素光谱比较确定太阳成分 | |
| C. | 根据α粒子散射实验,卢瑟福提出了原子核式模型,确定了一般原子核半径数量级为10-15m | |
| D. | 原子核的比结合能大小可反应原子核的稳定程度,该值随质量数的增加而增大 | |
| E. | 康普顿效应表明光子除了能量之外还有动量,揭示了光的粒子性 |
 A和B两个小球固定在一根轻杆的两端,此杆可绕穿过其中心的水平轴O无摩擦转动.现使轻杆从水平状态无初速度释放,发现杆绕O沿顺时针方向转动,则杆从释放起转动90°的过程中,错误的是( )
A和B两个小球固定在一根轻杆的两端,此杆可绕穿过其中心的水平轴O无摩擦转动.现使轻杆从水平状态无初速度释放,发现杆绕O沿顺时针方向转动,则杆从释放起转动90°的过程中,错误的是( )| A. | B球的重力势能减少,动能增加 | B. | A球的重力势能增加,动能减少 | ||
| C. | A球的重力势能和动能都增加了 | D. | A球和B球的总机械能是守恒的 |
 由不同介质制成的两个半径均为R的透明四分之一圆柱体I和Ⅱ紧靠在一起,截面如图所示,圆心为0,顶部交点为D,以O为原点建立直角坐标系xOy.红色光束1从介质I底部的A(-$\frac{{\sqrt{3}}}{2}$R,0)点垂直于界面入射;红色光束2平行于y轴向下射入介质Ⅱ,入射点为B且∠BOD=60°.已知透明介质I对红光的折射率n1=$\sqrt{2}$,透明介质Ⅱ对红光的折射率n2=$\sqrt{3}$.设光束1经柱面反射或折射后与y轴交点和光束2经柱体下底面折射后与y轴交点之间的距离为d.求:
由不同介质制成的两个半径均为R的透明四分之一圆柱体I和Ⅱ紧靠在一起,截面如图所示,圆心为0,顶部交点为D,以O为原点建立直角坐标系xOy.红色光束1从介质I底部的A(-$\frac{{\sqrt{3}}}{2}$R,0)点垂直于界面入射;红色光束2平行于y轴向下射入介质Ⅱ,入射点为B且∠BOD=60°.已知透明介质I对红光的折射率n1=$\sqrt{2}$,透明介质Ⅱ对红光的折射率n2=$\sqrt{3}$.设光束1经柱面反射或折射后与y轴交点和光束2经柱体下底面折射后与y轴交点之间的距离为d.求: 如图所示,真空中有一下表面镀反射膜的平行玻璃砖,其折射率n=$\sqrt{2}$,一束单色光与界面成θ=45°角斜射到玻璃砖表面上,最后在玻璃砖的右侧面竖直光屏上出现了两个光点A和B,A和B相距h=2.0cm.已知光在真空中的传播速度c=3.0×108m/s.试求:玻璃砖的厚度d(结果保留两位有效数字).
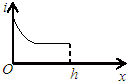
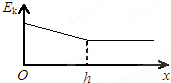
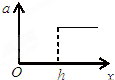
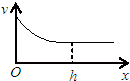
如图所示,真空中有一下表面镀反射膜的平行玻璃砖,其折射率n=$\sqrt{2}$,一束单色光与界面成θ=45°角斜射到玻璃砖表面上,最后在玻璃砖的右侧面竖直光屏上出现了两个光点A和B,A和B相距h=2.0cm.已知光在真空中的传播速度c=3.0×108m/s.试求:玻璃砖的厚度d(结果保留两位有效数字). 如图所示,开口向下的导线框固定在竖直平面内,上端有一开关,线框处于与其平面垂直的匀强磁场中,磁场的宽度为h.一导体棒开始时静止于A位置,然后释放,导体棒刚进入磁场时,关闭开关s.用x表示导体棒进入磁场后的位移,i表示棒中的感应电流大小,v表示导体棒的速度大小,Ek表示导体棒的动能,a表示导体棒的加速度大小,导体棒与线框的两个边垂直并接触良好.以下图象可能正确的是( )
如图所示,开口向下的导线框固定在竖直平面内,上端有一开关,线框处于与其平面垂直的匀强磁场中,磁场的宽度为h.一导体棒开始时静止于A位置,然后释放,导体棒刚进入磁场时,关闭开关s.用x表示导体棒进入磁场后的位移,i表示棒中的感应电流大小,v表示导体棒的速度大小,Ek表示导体棒的动能,a表示导体棒的加速度大小,导体棒与线框的两个边垂直并接触良好.以下图象可能正确的是( )