题目内容
11. 如图所示,真空中有一下表面镀反射膜的平行玻璃砖,其折射率n=$\sqrt{2}$,一束单色光与界面成θ=45°角斜射到玻璃砖表面上,最后在玻璃砖的右侧面竖直光屏上出现了两个光点A和B,A和B相距h=2.0cm.已知光在真空中的传播速度c=3.0×108m/s.试求:玻璃砖的厚度d(结果保留两位有效数字).
如图所示,真空中有一下表面镀反射膜的平行玻璃砖,其折射率n=$\sqrt{2}$,一束单色光与界面成θ=45°角斜射到玻璃砖表面上,最后在玻璃砖的右侧面竖直光屏上出现了两个光点A和B,A和B相距h=2.0cm.已知光在真空中的传播速度c=3.0×108m/s.试求:玻璃砖的厚度d(结果保留两位有效数字).
分析 一束光斜射在表面镀反射膜的平行玻璃砖,则反射光线在竖直光屏上出现光点A,而折射光线经反射后再折射在竖直光屏上出现光点B,根据光学的几何关系可由AB两点间距确定CE间距,再由折射定律,得出折射角,最终算出玻璃砖的厚度.
解答  解:由题,单色光与界面成θ=45°,入射角θ1=45°,根据折射率公式 n=$\frac{sin{θ}_{1}}{sin{θ}_{2}}$,
解:由题,单色光与界面成θ=45°,入射角θ1=45°,根据折射率公式 n=$\frac{sin{θ}_{1}}{sin{θ}_{2}}$,
得:sinθ2=$\frac{1}{2}$,θ2=30°
作出如图所示的光路,△CDE为等边三角形,四边形ABEC为梯形,CE=AB=h.玻璃的厚度d就是边长h的等边三角形的高.故有:
d=hcos30°=$\frac{\sqrt{3}}{2}h$=$\frac{\sqrt{3}}{2}×2.0$cm=$\sqrt{3}$cm=1.732cm
答:玻璃砖的厚度d为1.732cm.
点评 本题根据光路可逆原理及光的反射定律可以证明AC与BE平行,从而确定CE的长度.

练习册系列答案
相关题目
2.下列有关实验的描述中,正确的是( )
| A. | 在“验证力的平行四边形定则”的实验中,标记拉力方向时,要用铅笔紧靠细绳沿绳移动铅笔画出 | |
| B. | 在“探究弹力和弹簧伸长的关系”实验中,作出弹力和弹簧长度的关系图象也能求弹簧的劲度系数 | |
| C. | 在“探究功与速度变化的关系”的实验中,所选用的橡皮筋规格应相同 | |
| D. | 在“验证机械能守恒定律”的实验中,可以由公式v=gt求出打某点时纸带的速度 |
20. 如图所示,把小车放在水平桌面上,用轻绳跨过定滑轮使之与盛有沙子的小桶相连,已知小车的质量为M,小桶与沙子的总质量为m,把小车从静止状态释放后,在小桶下落竖直高度为h的过程中,若不计滑轮摩擦及空气的阻力,下列说法中正确的是( )
如图所示,把小车放在水平桌面上,用轻绳跨过定滑轮使之与盛有沙子的小桶相连,已知小车的质量为M,小桶与沙子的总质量为m,把小车从静止状态释放后,在小桶下落竖直高度为h的过程中,若不计滑轮摩擦及空气的阻力,下列说法中正确的是( )
 如图所示,把小车放在水平桌面上,用轻绳跨过定滑轮使之与盛有沙子的小桶相连,已知小车的质量为M,小桶与沙子的总质量为m,把小车从静止状态释放后,在小桶下落竖直高度为h的过程中,若不计滑轮摩擦及空气的阻力,下列说法中正确的是( )
如图所示,把小车放在水平桌面上,用轻绳跨过定滑轮使之与盛有沙子的小桶相连,已知小车的质量为M,小桶与沙子的总质量为m,把小车从静止状态释放后,在小桶下落竖直高度为h的过程中,若不计滑轮摩擦及空气的阻力,下列说法中正确的是( )| A. | 若增加沙子的质量,系统的加速度将趋于无穷大 | |
| B. | 若水平桌面光滑,m处于完全失重状态 | |
| C. | 若水平桌面光滑,小桶获得的动能为$\frac{{m}^{2}gh}{(m+M)}$ | |
| D. | 若水平桌面光滑,小桶获得的动能为mgh |
 如图所示,在光滑水平面上有一辆质量M=8kg的平板小车,车上有一个质量m=1.9kg的木块,木块距小车左端6m(木块可视为质点),车与木块一起以v=1m/s的速度水平向右匀速行驶.一颗质量m0=0.1kg的子弹以v0=179m/s的初速度水平向左飞来,瞬间击中木块并留在其中.如果木块刚好不从车上掉下来,求:
如图所示,在光滑水平面上有一辆质量M=8kg的平板小车,车上有一个质量m=1.9kg的木块,木块距小车左端6m(木块可视为质点),车与木块一起以v=1m/s的速度水平向右匀速行驶.一颗质量m0=0.1kg的子弹以v0=179m/s的初速度水平向左飞来,瞬间击中木块并留在其中.如果木块刚好不从车上掉下来,求: 将两个不同金属电极插入水果中就可以做成一个水果电池,但口常生活中我们很少用“水果电池”.这是为什么呢?某学习小组的同学准备就此问题进行探究.
将两个不同金属电极插入水果中就可以做成一个水果电池,但口常生活中我们很少用“水果电池”.这是为什么呢?某学习小组的同学准备就此问题进行探究.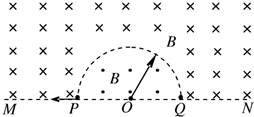 如图所示,直线MN下方无磁场,上方空间存在两个匀强磁场,其分界线是半径为R的半圆,两侧的磁场方向相反且垂直于纸面,磁感应强度大小都为B.现有一质量为m、电荷量为q的带负电微粒从P点沿半径方向向左侧射出,最终打到Q点,不计微粒的重力.求:
如图所示,直线MN下方无磁场,上方空间存在两个匀强磁场,其分界线是半径为R的半圆,两侧的磁场方向相反且垂直于纸面,磁感应强度大小都为B.现有一质量为m、电荷量为q的带负电微粒从P点沿半径方向向左侧射出,最终打到Q点,不计微粒的重力.求: 如图所示,质量分别为m1、m2的两小球A、B静止在光滑斜面的最低点和最高点,将B球从静止释放的同时,将A球以沿斜面向上的初速度v0射出.经t=0.5s时,两球相碰,碰撞时间极短,碰后两球粘在一起,恰好能到达斜面最高点.已知m1=2m2,斜面倾角为37°,重力加速度g=10m/s2,sin37°=0.6,忽略空气阻力.
如图所示,质量分别为m1、m2的两小球A、B静止在光滑斜面的最低点和最高点,将B球从静止释放的同时,将A球以沿斜面向上的初速度v0射出.经t=0.5s时,两球相碰,碰撞时间极短,碰后两球粘在一起,恰好能到达斜面最高点.已知m1=2m2,斜面倾角为37°,重力加速度g=10m/s2,sin37°=0.6,忽略空气阻力.