题目内容
16.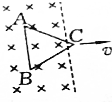 如图所示,把等边三角形ABC从垂直于它所在的平面的匀强磁场中匀速拉出,则在拉出过程中:
如图所示,把等边三角形ABC从垂直于它所在的平面的匀强磁场中匀速拉出,则在拉出过程中:(1)产生的感应电动势E是否为恒量?
(2)产生的感应电流是否均匀增加?
(3)感应电流的电功率是否均匀增加?
(4)穿过线框的磁通量是否均匀减小?
[提示:感应电均匀增加.答案:否;是;否;否.].
分析 (1)线圈切割磁感线,有效长度为线圈与磁场边界的两个交点间的距离,根据公式E=BLv判断;
(2)根据欧姆定律列式分析;
(3)根据P=$\frac{{E}^{2}}{r}$列式分析;
(4)采用假设法分析,即假设磁通量均匀减小,根据法拉第电磁感应定律得到矛盾结论.
解答 解:(1)线圈切割磁感线的有效长度等于三角形ABC与磁场右边界的两交点间的距离,因为在磁场中AB切割、AC与BC部分切割,AC与BC在磁场中部分与AB的一部分的有效长度是对称的,电动势抵消了;故有效长度就是三角形与磁场边界的两个交点间的距离,该长度在均匀增加,根据E=BLv,感应电动势也就是均匀增加;
(2)感应电动势在均匀增加,根据I=$\frac{E}{R}$,感应电流也就均匀增加;
(3)感应电动势在均匀增加,根据P=$\frac{{E}^{2}}{r}$,感应电流的电功率不是均匀增加;
(4)假设磁通量均匀减小,根据法拉第电磁感应定律,任意时间内的平均感应电动势不变,故瞬时感应电动势不变,矛盾,也就说明穿过线框的磁通量不是均匀减小;
答:(1)产生的感应电动势E不是恒量;
(2)产生的感应电流均匀增加;
(3)感应电流的电功率不是均匀增加;
(4)穿过线框的磁通量也不是均匀减小.
点评 本题关键是结合法拉第电磁感应定律的两个公式进行分析,注意E=n$\frac{△∅}{△t}$可以求解平均值,E=BLv可以求解瞬时值,不难.

练习册系列答案
相关题目
6. 如图所示,先后以速度v1和v2匀速把一矩形线圈拉出有界的匀强磁场区域,v2=2v1,在先后两种情况下( )
如图所示,先后以速度v1和v2匀速把一矩形线圈拉出有界的匀强磁场区域,v2=2v1,在先后两种情况下( )
 如图所示,先后以速度v1和v2匀速把一矩形线圈拉出有界的匀强磁场区域,v2=2v1,在先后两种情况下( )
如图所示,先后以速度v1和v2匀速把一矩形线圈拉出有界的匀强磁场区域,v2=2v1,在先后两种情况下( )| A. | 线圈中的感应电流之比I1:I2=1:2 | |
| B. | 作用在线圈上的外力大小之比F1:F2=1:2 | |
| C. | 线圈中产生的焦耳热之比Q1:Q2=2:1 | |
| D. | 通过线圈某一截面的电荷量之比q1:q2=1:1 |
7. 如图所示,带电量为q的正点电荷靠近接地的大金属板,产生类似等量异种电荷产生的电场,点电荷q与金属板间的距离为d,那么点电荷q受到的电场力为( )
如图所示,带电量为q的正点电荷靠近接地的大金属板,产生类似等量异种电荷产生的电场,点电荷q与金属板间的距离为d,那么点电荷q受到的电场力为( )
 如图所示,带电量为q的正点电荷靠近接地的大金属板,产生类似等量异种电荷产生的电场,点电荷q与金属板间的距离为d,那么点电荷q受到的电场力为( )
如图所示,带电量为q的正点电荷靠近接地的大金属板,产生类似等量异种电荷产生的电场,点电荷q与金属板间的距离为d,那么点电荷q受到的电场力为( )| A. | k$\frac{{q}^{2}}{{d}^{2}}$ | B. | k$\frac{{q}^{2}}{2{d}^{2}}$ | ||
| C. | k$\frac{{q}^{2}}{4{d}^{2}}$ | D. | 以上三个答案均错误 |
4. 如图,在水平面内有四根相同的均匀光滑金属杆ab、ac、de以及df,其中ab、ac在a点固连,de、df在d点固连,分别构成两个“V”字型导轨,空间中存在垂直于水平面的匀强磁场,用力使导轨edf匀速向右运动,从图示位置开始计时,运动过程中两导轨的角平分线始终重合,导轨间接触始终良好,下列物理量随时间的变化关系正确的是( )
如图,在水平面内有四根相同的均匀光滑金属杆ab、ac、de以及df,其中ab、ac在a点固连,de、df在d点固连,分别构成两个“V”字型导轨,空间中存在垂直于水平面的匀强磁场,用力使导轨edf匀速向右运动,从图示位置开始计时,运动过程中两导轨的角平分线始终重合,导轨间接触始终良好,下列物理量随时间的变化关系正确的是( )
 如图,在水平面内有四根相同的均匀光滑金属杆ab、ac、de以及df,其中ab、ac在a点固连,de、df在d点固连,分别构成两个“V”字型导轨,空间中存在垂直于水平面的匀强磁场,用力使导轨edf匀速向右运动,从图示位置开始计时,运动过程中两导轨的角平分线始终重合,导轨间接触始终良好,下列物理量随时间的变化关系正确的是( )
如图,在水平面内有四根相同的均匀光滑金属杆ab、ac、de以及df,其中ab、ac在a点固连,de、df在d点固连,分别构成两个“V”字型导轨,空间中存在垂直于水平面的匀强磁场,用力使导轨edf匀速向右运动,从图示位置开始计时,运动过程中两导轨的角平分线始终重合,导轨间接触始终良好,下列物理量随时间的变化关系正确的是( )| A. |  拉力F与时间t的关系 | B. |  发热功率P与时间t的关系 | ||
| C. |  回路电阻R与时间t的关系 | D. |  电流I与时间t的关系 |
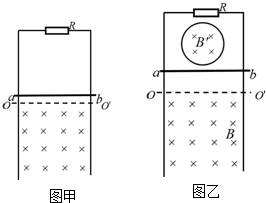
1. 光滑金属导轨L=0.5m,电阻不计,均匀变化的磁场充满整个轨道平面,如图甲所示.磁场的磁感应强度随时间变化的情况如图乙所示.金属棒ab的电阻为2Ω,垂直固定在导轨上静止不动,且与导轨左端距离l=0.2m.则( )
光滑金属导轨L=0.5m,电阻不计,均匀变化的磁场充满整个轨道平面,如图甲所示.磁场的磁感应强度随时间变化的情况如图乙所示.金属棒ab的电阻为2Ω,垂直固定在导轨上静止不动,且与导轨左端距离l=0.2m.则( )
 光滑金属导轨L=0.5m,电阻不计,均匀变化的磁场充满整个轨道平面,如图甲所示.磁场的磁感应强度随时间变化的情况如图乙所示.金属棒ab的电阻为2Ω,垂直固定在导轨上静止不动,且与导轨左端距离l=0.2m.则( )
光滑金属导轨L=0.5m,电阻不计,均匀变化的磁场充满整个轨道平面,如图甲所示.磁场的磁感应强度随时间变化的情况如图乙所示.金属棒ab的电阻为2Ω,垂直固定在导轨上静止不动,且与导轨左端距离l=0.2m.则( )| A. | 1s末回路中的电动势为0.l5V | B. | 1s末回路中的电流为1A | ||
| C. | 2s内回路产生的电热为0.01J | D. | 2s末,ab所受安培力大小为0.1N |
8. 有一体育娱乐比赛项目,其赛道俯视图如图所示,三根长度均为R的拦阻杆的一端固定在水平面上的O点,并能绕O点以角速度ω逆时针匀速转动,拦阻杆间的夹角为120°.AB为拦阻杆转动平面下方的一段水平传送带,传送带以速度v0匀速运动,方向如图所示,拦阻杆能够拦阻传送带的长度为$\sqrt{3}$R.若参赛者从A端踏上传送带,在传送带上不能与拦阻杆相遇,顺利到达B端即为赢得比赛.则参赛者相对传送带的最小运动速度为( )
有一体育娱乐比赛项目,其赛道俯视图如图所示,三根长度均为R的拦阻杆的一端固定在水平面上的O点,并能绕O点以角速度ω逆时针匀速转动,拦阻杆间的夹角为120°.AB为拦阻杆转动平面下方的一段水平传送带,传送带以速度v0匀速运动,方向如图所示,拦阻杆能够拦阻传送带的长度为$\sqrt{3}$R.若参赛者从A端踏上传送带,在传送带上不能与拦阻杆相遇,顺利到达B端即为赢得比赛.则参赛者相对传送带的最小运动速度为( )
 有一体育娱乐比赛项目,其赛道俯视图如图所示,三根长度均为R的拦阻杆的一端固定在水平面上的O点,并能绕O点以角速度ω逆时针匀速转动,拦阻杆间的夹角为120°.AB为拦阻杆转动平面下方的一段水平传送带,传送带以速度v0匀速运动,方向如图所示,拦阻杆能够拦阻传送带的长度为$\sqrt{3}$R.若参赛者从A端踏上传送带,在传送带上不能与拦阻杆相遇,顺利到达B端即为赢得比赛.则参赛者相对传送带的最小运动速度为( )
有一体育娱乐比赛项目,其赛道俯视图如图所示,三根长度均为R的拦阻杆的一端固定在水平面上的O点,并能绕O点以角速度ω逆时针匀速转动,拦阻杆间的夹角为120°.AB为拦阻杆转动平面下方的一段水平传送带,传送带以速度v0匀速运动,方向如图所示,拦阻杆能够拦阻传送带的长度为$\sqrt{3}$R.若参赛者从A端踏上传送带,在传送带上不能与拦阻杆相遇,顺利到达B端即为赢得比赛.则参赛者相对传送带的最小运动速度为( )| A. | v=$\frac{3\sqrt{3}Rω+2π{v}_{0}}{2π}$ | B. | v=$\frac{3\sqrt{3}Rω+4π{v}_{0}}{4π}$ | C. | v=$\frac{3\sqrt{3}Rω-4π{v}_{0}}{4π}$ | D. | v=$\frac{3\sqrt{3}Rω}{4π}$ |