题目内容
1. 光滑金属导轨L=0.5m,电阻不计,均匀变化的磁场充满整个轨道平面,如图甲所示.磁场的磁感应强度随时间变化的情况如图乙所示.金属棒ab的电阻为2Ω,垂直固定在导轨上静止不动,且与导轨左端距离l=0.2m.则( )
光滑金属导轨L=0.5m,电阻不计,均匀变化的磁场充满整个轨道平面,如图甲所示.磁场的磁感应强度随时间变化的情况如图乙所示.金属棒ab的电阻为2Ω,垂直固定在导轨上静止不动,且与导轨左端距离l=0.2m.则( )| A. | 1s末回路中的电动势为0.l5V | B. | 1s末回路中的电流为1A | ||
| C. | 2s内回路产生的电热为0.01J | D. | 2s末,ab所受安培力大小为0.1N |
分析 由图得到磁感应强度B的变化率,由法拉第电磁感应定律求感应电动势,由欧姆定律求出感应电流,由焦耳定律求电热.由F=BIL求出安培力.
解答 解:A、由图知,$\frac{△B}{△t}$=1T/s,由法拉第电磁感应定律得:感应电动势为 E=S$\frac{△B}{△t}$=Ll $\frac{△B}{△t}$=0.5×0.2×1V=0.1V,故A错误.
B、回路中感应电流为 I=$\frac{E}{R}$=$\frac{0.1}{2}$A=0.05A,故B错误.
C、2s内回路产生的电热为 Q=I2Rt=0.052×2×2J=0.01J,故C正确.
D、2s末,B=2T,ab所受的安培力为 F=BIL=2×0.01×0.5N=0.01N,故D错误.
故选:C
点评 本题关键是对图象的识别和应用,要利用好图象的斜率,结合电磁感应的基本规律:法拉第电磁感应定律、欧姆定律等研究.

练习册系列答案
相关题目
11. 如图所示,abcd为一矩形金属线框,其中ab=cd=L,ab边接有定值电阻R,cd边的质量为m,其他部分电阻和质量均不计,整个装置用两根绝缘轻弹簧悬挂起来.线框下方处在磁感应强度为B的匀强磁场中,磁场方向垂直于纸面向里.初始时刻,两根弹簧处于自然长度,给线框一竖直向下的初速度v0,当cd边第一次运动到最下端的过程中,R产生的热量为Q,此过程cd边始终未离开磁场.已知重力加速度大小为g,下列说法正确的是( )
如图所示,abcd为一矩形金属线框,其中ab=cd=L,ab边接有定值电阻R,cd边的质量为m,其他部分电阻和质量均不计,整个装置用两根绝缘轻弹簧悬挂起来.线框下方处在磁感应强度为B的匀强磁场中,磁场方向垂直于纸面向里.初始时刻,两根弹簧处于自然长度,给线框一竖直向下的初速度v0,当cd边第一次运动到最下端的过程中,R产生的热量为Q,此过程cd边始终未离开磁场.已知重力加速度大小为g,下列说法正确的是( )
 如图所示,abcd为一矩形金属线框,其中ab=cd=L,ab边接有定值电阻R,cd边的质量为m,其他部分电阻和质量均不计,整个装置用两根绝缘轻弹簧悬挂起来.线框下方处在磁感应强度为B的匀强磁场中,磁场方向垂直于纸面向里.初始时刻,两根弹簧处于自然长度,给线框一竖直向下的初速度v0,当cd边第一次运动到最下端的过程中,R产生的热量为Q,此过程cd边始终未离开磁场.已知重力加速度大小为g,下列说法正确的是( )
如图所示,abcd为一矩形金属线框,其中ab=cd=L,ab边接有定值电阻R,cd边的质量为m,其他部分电阻和质量均不计,整个装置用两根绝缘轻弹簧悬挂起来.线框下方处在磁感应强度为B的匀强磁场中,磁场方向垂直于纸面向里.初始时刻,两根弹簧处于自然长度,给线框一竖直向下的初速度v0,当cd边第一次运动到最下端的过程中,R产生的热量为Q,此过程cd边始终未离开磁场.已知重力加速度大小为g,下列说法正确的是( )| A. | 初始时刻cd边所受安培力的大小为$\frac{{B}^{2}{L}^{2}{v}_{0}}{R}$-mg | |
| B. | 线框中产生的最大感应电流大于$\frac{BL{v}_{0}}{R}$ | |
| C. | cd边第一次达到最下端的时刻,两根弹簧的弹性势能总量大于$\frac{m{{v}_{0}}^{2}}{2}$-Q | |
| D. | 在cd边反复运动过程中,R中产生的电热最多为$\frac{m{{v}_{0}}^{2}}{2}$ |
9. 如图所示,平行金属导轨与水平面间的夹角为θ,导轨电阻不计,并与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感应强度大小为B.有一质量为m、长为l的导体棒从ab位置获得平行于斜面的、大小为v的初速度向上运动,最远到达a'b'的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )
如图所示,平行金属导轨与水平面间的夹角为θ,导轨电阻不计,并与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感应强度大小为B.有一质量为m、长为l的导体棒从ab位置获得平行于斜面的、大小为v的初速度向上运动,最远到达a'b'的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )
 如图所示,平行金属导轨与水平面间的夹角为θ,导轨电阻不计,并与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感应强度大小为B.有一质量为m、长为l的导体棒从ab位置获得平行于斜面的、大小为v的初速度向上运动,最远到达a'b'的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )
如图所示,平行金属导轨与水平面间的夹角为θ,导轨电阻不计,并与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感应强度大小为B.有一质量为m、长为l的导体棒从ab位置获得平行于斜面的、大小为v的初速度向上运动,最远到达a'b'的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )| A. | 上滑过程中导体棒受到的最大安培力为$\frac{{B}^{2}{l}^{2}v}{2R}$ | |
| B. | 上滑过程中通过电阻R的电量为$\frac{Bls}{R}$ | |
| C. | 上滑过程中导体棒克服安培力做的功为$\frac{1}{2}$ mv2-mgs(sin θ+μcos θ) | |
| D. | 上滑过程中导体棒损失的机械能为$\frac{1}{2}$mv2-mgssin θ |
 如图所示装置由水平轨道、倾角θ=37°的倾角轨道连接而成,轨道所在空间存在磁感应强度大小为B=0.1T、方向竖直向上的匀强磁场.质量m=0.035kg、长度L=0.1m、电阻R=0.025Ω的导体棒ab置于倾斜轨道上,刚好不下滑;质量、长度、电阻与棒ab相同的光滑导体棒cd置于水平轨道上,用恒力F=2.0N拉棒cd,使之在水平轨道上向右运动.棒ab、cd与导轨垂直,且两端与导轨保持良好接触,最大静摩擦力等于滑动摩擦力,sin37°=0.6,cos37°=0.8,取g=10m/s2.
如图所示装置由水平轨道、倾角θ=37°的倾角轨道连接而成,轨道所在空间存在磁感应强度大小为B=0.1T、方向竖直向上的匀强磁场.质量m=0.035kg、长度L=0.1m、电阻R=0.025Ω的导体棒ab置于倾斜轨道上,刚好不下滑;质量、长度、电阻与棒ab相同的光滑导体棒cd置于水平轨道上,用恒力F=2.0N拉棒cd,使之在水平轨道上向右运动.棒ab、cd与导轨垂直,且两端与导轨保持良好接触,最大静摩擦力等于滑动摩擦力,sin37°=0.6,cos37°=0.8,取g=10m/s2.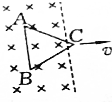 如图所示,把等边三角形ABC从垂直于它所在的平面的匀强磁场中匀速拉出,则在拉出过程中:
如图所示,把等边三角形ABC从垂直于它所在的平面的匀强磁场中匀速拉出,则在拉出过程中:
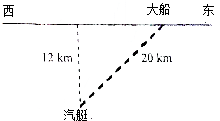 大船在海面上沿由东向西的航道以20km/h的速度航行,船西偏南某方向有一汽艇距离大船20km,距离航道12km,则汽艇速度至少为12km/h才能追到大船,若汽艇速度为15km/h,则至少要0.8h才能追上大船.
大船在海面上沿由东向西的航道以20km/h的速度航行,船西偏南某方向有一汽艇距离大船20km,距离航道12km,则汽艇速度至少为12km/h才能追到大船,若汽艇速度为15km/h,则至少要0.8h才能追上大船. 如图所示,一根弹性杆的一端固定在倾角为30°的斜面上,杆的另一端固定一个重为5N的小球.小球处于静止状态,则弹性杆对小球的弹力大小为5N,方向竖直向上.
如图所示,一根弹性杆的一端固定在倾角为30°的斜面上,杆的另一端固定一个重为5N的小球.小球处于静止状态,则弹性杆对小球的弹力大小为5N,方向竖直向上.