题目内容
12.设宇航员在某星球上从高32m处自由释放一重物,测得在下落第1s内所通过的距离为4m,则重物下落的时间是2$\sqrt{2}$s,该重物在下落后2s末的速度是16m/s.分析 根据第一秒下落的高度求得下落的加速度,利用位移时间公式求得下落时间,根据vat求得速度
解答 解:物体在该星球表面做自由落体运动,根据$h=\frac{1}{2}a{t}^{2}$可知:a=$\frac{2h}{{t}^{2}}=\frac{2×4}{{1}^{2}}m/{s}^{2}=8m/{s}^{2}$
下落的时间为:$t′=\sqrt{\frac{2H}{a}}=\sqrt{\frac{2×32}{8}}s=2\sqrt{2}s$
2s末的速度为:v=at″=8×2m/s=16m/s
故答案为:$2\sqrt{2}$,16
点评 解决本题的关键掌握自由落体运动的位移时间公式.自由落体运动规律在其他星球照样适用.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
2.2016年中秋夜,我国成功将天宫二号送入预定轨道,2016年10月17日神舟十一号顺利升空并在之后与天宫二号实行交会对接.天宫二号是在天宫一号基础上研制的航天器,两者外形完全相同,但却承担着不同的任务. 天宫一号主要是和载人飞船配合完成空间交会对接实验任务,而天宫二号则是我国第一个具备太空补加功能的载人航天实验室,要第一次实现航天员中期驻留、第一次试验推进剂太空补加技术等重要的科学实验,天宫二号被称为是我国首个真正意义上的空间实验室.天宫二号的轨道高度为393km,比天宫一号高了50km,关于天宫二号与天宫一号的比较,以下说法正确的是( )
| A. | “天宫二号”运行的线速度比“天宫一号”小 | |
| B. | “天宫二号”运行的加速度比“天宫一号”小 | |
| C. | “天宫二号”运行的角速度比“天宫一号”小 | |
| D. | “天宫二号”运行的周期比“天宫一号”小 |
3.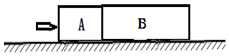 在水平面上并排固定着两块材料相同的木块A、B,木块B的长度是木块A的2倍,如图所示.一子弹水平射入两木块,穿出B木块后速度恰好为零.子弹在木块中可认为是匀减速运动关于子弹的运动下列说法正确的是( )
在水平面上并排固定着两块材料相同的木块A、B,木块B的长度是木块A的2倍,如图所示.一子弹水平射入两木块,穿出B木块后速度恰好为零.子弹在木块中可认为是匀减速运动关于子弹的运动下列说法正确的是( )
 在水平面上并排固定着两块材料相同的木块A、B,木块B的长度是木块A的2倍,如图所示.一子弹水平射入两木块,穿出B木块后速度恰好为零.子弹在木块中可认为是匀减速运动关于子弹的运动下列说法正确的是( )
在水平面上并排固定着两块材料相同的木块A、B,木块B的长度是木块A的2倍,如图所示.一子弹水平射入两木块,穿出B木块后速度恰好为零.子弹在木块中可认为是匀减速运动关于子弹的运动下列说法正确的是( )| A. | 射入木块A和木块B时的速度之比为$\sqrt{3}$:$\sqrt{2}$ | |
| B. | 在木块A和木块B中运动时间之比为($\sqrt{2}$-1):1 | |
| C. | 在木块A和木块B中运动时的加速度之比为1:2 | |
| D. | 在木块A和木块B中运动时的平均速度之比为($\sqrt{3}$+$\sqrt{2}$):$\sqrt{2}$ |
20.下列哪组力共点力的合成不可能为零( )
| A. | 6N,7N,9N | B. | 3N,5N,5N | C. | 2N,4N,6N | D. | 3N,4N,8N |
7.某物体作直线运动的速度一时间图象如图 所示.由图可知( )


| A. | 0至6s物体的速度方向没有改变 | B. | 4至6s物体向负方向运动 | ||
| C. | 0至6s物体的加速度方向没有改变 | D. | 4至6s物体的加速度为-2m/s2 |
17.将一本书水平放在桌面上静止,则下列说法正确的是( )
| A. | 书对桌面的压力就是书受到的重力,施力物体是地球 | |
| B. | 书对桌面的压力是由于桌面的形变引起的 | |
| C. | 书放在桌面上对桌面施加了弹力,但桌面没有发生形变 | |
| D. | 书对桌面的压力是弹力,在数值上等于书受到的重力 |
1.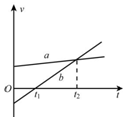 A、B两物体在同一直线上从某点开始计时的速度图象如图中的a、b所示,则由图可知,在0到t2时间内( )
A、B两物体在同一直线上从某点开始计时的速度图象如图中的a、b所示,则由图可知,在0到t2时间内( )
 A、B两物体在同一直线上从某点开始计时的速度图象如图中的a、b所示,则由图可知,在0到t2时间内( )
A、B两物体在同一直线上从某点开始计时的速度图象如图中的a、b所示,则由图可知,在0到t2时间内( )| A. | A、B运动始终同向,B比A运动得快 | |
| B. | 在t1时刻,A、B相距最远,B开始反向 | |
| C. | A、B的加速度始终同向,B比A的加速度大 | |
| D. | 在t2时刻,A、B并未相遇,只是速度相同 |
 某实验小组设计了如图所示的实验装置探究加速度与力、质量的关系,开始时闭合开关,电磁铁将A、B两个小车吸住,断开开关,两小车同时在细绳拉力作用下在水平桌面沿同一直线相向运动.实验中始终保持小车质量远大于托盘和砝码的质量,实验装置中各部分摩擦阻力可忽略不计.
某实验小组设计了如图所示的实验装置探究加速度与力、质量的关系,开始时闭合开关,电磁铁将A、B两个小车吸住,断开开关,两小车同时在细绳拉力作用下在水平桌面沿同一直线相向运动.实验中始终保持小车质量远大于托盘和砝码的质量,实验装置中各部分摩擦阻力可忽略不计.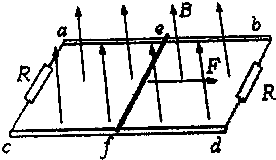 如图所示,两根间距L=1.0m、足够长平行光滑金属导轨ab、cd水平放置,两端均与阻值R=2.0Ω的电阻相连.质量m=0.2kg的导体棒ef在恒定外力F作用下由静止开始运动,导体棒长度与两导轨间距相等,导体棒电阻为r=1.0Ω,整个装置处于垂直于导轨平面向上的匀强磁场B中,导体棒运动过程中与金属导轨接触良好(两导轨及导线电阻不计).求:
如图所示,两根间距L=1.0m、足够长平行光滑金属导轨ab、cd水平放置,两端均与阻值R=2.0Ω的电阻相连.质量m=0.2kg的导体棒ef在恒定外力F作用下由静止开始运动,导体棒长度与两导轨间距相等,导体棒电阻为r=1.0Ω,整个装置处于垂直于导轨平面向上的匀强磁场B中,导体棒运动过程中与金属导轨接触良好(两导轨及导线电阻不计).求: