题目内容
14.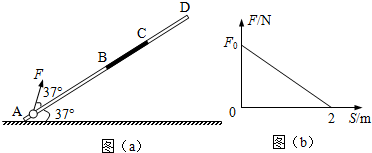 如图(a)所示,固定直杆AD与水平地面成37°角,长度分别为2m和1m的AB段和CD段光滑,长为1m的BC段粗糙.质量为1kg的小球套在直杆上,在方向与直杆成37°角的力F作用下,从杆底端A点处由静止开始运动,小球恰能到达顶端D点.已知力F与小球位移的大小关系如图(b)所示,球与BC段间的动摩擦因数为0.1,sin37°=0.6,cos37°=0.8,取g=10m/s2.求:
如图(a)所示,固定直杆AD与水平地面成37°角,长度分别为2m和1m的AB段和CD段光滑,长为1m的BC段粗糙.质量为1kg的小球套在直杆上,在方向与直杆成37°角的力F作用下,从杆底端A点处由静止开始运动,小球恰能到达顶端D点.已知力F与小球位移的大小关系如图(b)所示,球与BC段间的动摩擦因数为0.1,sin37°=0.6,cos37°=0.8,取g=10m/s2.求:(1)小球向上运动到B点时的速度vB;
(2)图(b)中F0的大小;
(3)以地面为零势能点,求小球重力势能为15J时的动能Ek.
分析 (1)分析小球从B运动到D的过程,摩擦力和重力做负功,由动能定理求出小球向上运动到B点时的速度vB;
(2)分析小球从A运动到B的过程,力F做正功,重力做负功,由动能定理求出力F做的功WF,再求出F0;
(3)先找出小球重力势能为15J时位置,再根据动能定理求出向上和向下经过该位置的动能.
解答 解:(1)小球从B运动到D的过程中,摩擦力和重力做负功,由动能定理得:
-mghBD-μmgcos37°sBC=0-$\frac{1}{2}$mvB2
代入数据,解得:vB≈5.06m/s;
(2)A到B的过程中,力F做正功,重力做负功,由动能定理有:
WF-mghAB=$\frac{1}{2}$mvB2
代入数据,解得:WF=24.8J
因为WF=$\frac{1}{2}$F0sABcos37°
得:F0=31N;
(3)设E点处重力势能为15J,则有:
mgsAEsin37°=15J
则sAE=2.5m
①球向上运动经过该处时,从B到E的过程,由动能定理有:
-mghBE-μmgcos37°sBE=Ek-$\frac{1}{2}$mvB2
代入数据得:Ek=9.4J
②球向下运动经过该处时,从D到E的过程,由动能定理有:
mghBE-μmgcos37°sCE=Ek?
代入数据得:Ek?=8.6J
答:(1)小球向上运动到B点时的速度vB为5.06m/s;
(2)图(b)中F0的大小为31N;
(3)以地面为零势能点,小球重力势能为15J时,①球向上运动经过该处时的动能Ek为9.4J;②球向下运动经过该处时的动能Ek为8.6J.
点评 本题考查动能定理的应用,解题关键是合理选择运动过程,分析各力做功情况,再利用动能定理列式,第(3)问要注意不要遗漏,要考虑小球向上和向下经过该点的动能.

练习册系列答案
相关题目
4.“神舟十号”飞船发射后,经过多次变轨进入距地面高度为h的圆形轨道.已知飞船质量为m,地球半径为R,地球表面的重力加速度为g.设飞船进入圆形轨道后运动时的动能为EK,则( )
| A. | Ek=$\frac{mg{R}^{2}}{2(R+h)}$ | B. | Ek=$\frac{1}{2}$mg(R+h) | C. | Ek=$\frac{1}{2}$mgR | D. | Ek=mgh |
5.如图甲所示,理想变压器原、副线圈的匝数比为5﹕l, 、R和L分别是电压表、定值电阻和电感线圈,D1、D2均为灯泡.已知原线圈两端电压u按图乙所示正弦规律变化,下列说法正确的是( )
、R和L分别是电压表、定值电阻和电感线圈,D1、D2均为灯泡.已知原线圈两端电压u按图乙所示正弦规律变化,下列说法正确的是( )

 、R和L分别是电压表、定值电阻和电感线圈,D1、D2均为灯泡.已知原线圈两端电压u按图乙所示正弦规律变化,下列说法正确的是( )
、R和L分别是电压表、定值电阻和电感线圈,D1、D2均为灯泡.已知原线圈两端电压u按图乙所示正弦规律变化,下列说法正确的是( )
| A. | 电压表示数为62.2V | |
| B. | 电压u的表达式u=311sin100πt(V) | |
| C. | 仅增大电压u的频率,电压表示数增大 | |
| D. | 仅增大电压u的频率,D1亮度不变,D2变暗 |
2.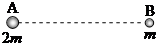 相距为d、质量分别为2m和m的两颗恒星A和B组成双星系统,在万有引力作用下各自绕它们连线上的某一固定点,在同一平面内做匀速圆周运动.设两颗恒星的转动半径分别为RA、RB,速度大小分别为vA、vB,动能分别为EkA、EkB,引力常量为G,则下列关系中正确的是( )
相距为d、质量分别为2m和m的两颗恒星A和B组成双星系统,在万有引力作用下各自绕它们连线上的某一固定点,在同一平面内做匀速圆周运动.设两颗恒星的转动半径分别为RA、RB,速度大小分别为vA、vB,动能分别为EkA、EkB,引力常量为G,则下列关系中正确的是( )
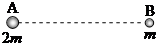 相距为d、质量分别为2m和m的两颗恒星A和B组成双星系统,在万有引力作用下各自绕它们连线上的某一固定点,在同一平面内做匀速圆周运动.设两颗恒星的转动半径分别为RA、RB,速度大小分别为vA、vB,动能分别为EkA、EkB,引力常量为G,则下列关系中正确的是( )
相距为d、质量分别为2m和m的两颗恒星A和B组成双星系统,在万有引力作用下各自绕它们连线上的某一固定点,在同一平面内做匀速圆周运动.设两颗恒星的转动半径分别为RA、RB,速度大小分别为vA、vB,动能分别为EkA、EkB,引力常量为G,则下列关系中正确的是( )| A. | RA=2RB | B. | vA=2vB | C. | EkA=EkB | D. | EkA+EkB=$\frac{G{m}^{2}}{d}$ |
19. 如图电路中,电源的电动势E和内阻r均为定值,R1R2为滑动变阻器,R0为定值电阻.当变阻器的阻值发生变化时,以下推断正确的是( )
如图电路中,电源的电动势E和内阻r均为定值,R1R2为滑动变阻器,R0为定值电阻.当变阻器的阻值发生变化时,以下推断正确的是( )
 如图电路中,电源的电动势E和内阻r均为定值,R1R2为滑动变阻器,R0为定值电阻.当变阻器的阻值发生变化时,以下推断正确的是( )
如图电路中,电源的电动势E和内阻r均为定值,R1R2为滑动变阻器,R0为定值电阻.当变阻器的阻值发生变化时,以下推断正确的是( )| A. | 若只增大R1,则R0消耗的功率一定减小 | |
| B. | 若只增大R2,则R1消耗的功率一定变小 | |
| C. | 若只减小R1,则R1消耗的功率一定变小 | |
| D. | 若只减小R2,则电源的输出功率一定变小 |
3.某直流电动机的线圈电阻阻值为R,电动机正常工作时,两端的电压为U,通过线圈的电流为I,若工作时间为t,则下列关于电动机消耗的电能的说法正确的是( )
| A. | 电动机消耗的电能为I2Rt | B. | 电动机消耗的电能为UIt | ||
| C. | 电动机消耗的电能为$\frac{U^2}{R}$t | D. | 电动机消耗的电能小于I2Rt |
4.如图甲所示,理想变压器原、副线圈的匝数比为10:1,原线圈接交流电源和交流电压表、交流电流表,副线圈通过电阻为R的导线与热水器、抽油烟机连接.已知原线圈两端的电压保持不变,副线圈上的电压按如图乙所示规律变化,现闭合开关S接通抽油烟机,下列说法正确的是( )


| A. | 热水器两端电压的瞬时值表达式为u=220$\sqrt{2}$sin(100πt)V | |
| B. | 电压表示数为2200V | |
| C. | 电流表示数变大 | |
| D. | 变压器的输入功率增大 |

 如图所示,在光滑的水平地面上,质量为M的足够长木板和质量为m的小木块(可看作质点)一起以共同的速度v0向右匀速滑行,与右边的竖直墙壁发生碰撞后木板以原速率返回.若小木块与长木板间的动摩擦因数为μ,M>m,试求小木块在长木板上相对长木板滑行的时间.
如图所示,在光滑的水平地面上,质量为M的足够长木板和质量为m的小木块(可看作质点)一起以共同的速度v0向右匀速滑行,与右边的竖直墙壁发生碰撞后木板以原速率返回.若小木块与长木板间的动摩擦因数为μ,M>m,试求小木块在长木板上相对长木板滑行的时间.