题目内容
6. 如图所示,在光滑的水平地面上,质量为M的足够长木板和质量为m的小木块(可看作质点)一起以共同的速度v0向右匀速滑行,与右边的竖直墙壁发生碰撞后木板以原速率返回.若小木块与长木板间的动摩擦因数为μ,M>m,试求小木块在长木板上相对长木板滑行的时间.
如图所示,在光滑的水平地面上,质量为M的足够长木板和质量为m的小木块(可看作质点)一起以共同的速度v0向右匀速滑行,与右边的竖直墙壁发生碰撞后木板以原速率返回.若小木块与长木板间的动摩擦因数为μ,M>m,试求小木块在长木板上相对长木板滑行的时间.
分析 木块与木板组成的系统动量守恒,应用动量守恒定律求出共同速度,然后应用动量定理可以求出时间.
解答 解:设木块和木板最后的共同速度为v,木板与墙壁碰撞后,以向右为正方向,由动量守恒定律有:Mv0-mv0=(M+m)v
以向左的方向为正方向,设碰撞后经时间t木块与木板具有共同速度,由动量定理可得:μmgt=mv-(-mv0)
由以上两式可得:t=$\frac{2Mv0}{μg(M+m)}$.
答:小木块在长木板上相对长木板滑行的时间为$\frac{2Mv0}{μg(M+m)}$.
点评 本题考查了动量守恒定律与动量定理的应用,分析清楚物体运动过程是正确解题的关键,应用动量守恒定律与动量定理可以解题,解题时要注意正方向的选择.

练习册系列答案
相关题目
17.物理学中,力的分解、平均速度、总电阻所蕴含的共同的科学思想是( )
| A. | 比值定义 | B. | 等效替代 | C. | 控制变量 | D. | 理想模型 |
18. 手摇发电机产生的正弦交流电经变压器给灯泡L供电,其电路如图.当线圈以角速度ω匀速转动时,电压表示数为U,灯泡正常发光.已知发电机线圈的电阻为r,灯泡正常发光时的电阻为R,其它电阻可忽略,变压器原线圈与副线圈的匝数比为k,变压器可视为理想变压器.则( )
手摇发电机产生的正弦交流电经变压器给灯泡L供电,其电路如图.当线圈以角速度ω匀速转动时,电压表示数为U,灯泡正常发光.已知发电机线圈的电阻为r,灯泡正常发光时的电阻为R,其它电阻可忽略,变压器原线圈与副线圈的匝数比为k,变压器可视为理想变压器.则( )
 手摇发电机产生的正弦交流电经变压器给灯泡L供电,其电路如图.当线圈以角速度ω匀速转动时,电压表示数为U,灯泡正常发光.已知发电机线圈的电阻为r,灯泡正常发光时的电阻为R,其它电阻可忽略,变压器原线圈与副线圈的匝数比为k,变压器可视为理想变压器.则( )
手摇发电机产生的正弦交流电经变压器给灯泡L供电,其电路如图.当线圈以角速度ω匀速转动时,电压表示数为U,灯泡正常发光.已知发电机线圈的电阻为r,灯泡正常发光时的电阻为R,其它电阻可忽略,变压器原线圈与副线圈的匝数比为k,变压器可视为理想变压器.则( )| A. | 灯泡的额定电压为$\frac{U}{k}$ | |
| B. | 灯泡的额定功率为$\frac{{k}^{2}{U}^{2}}{R}$ | |
| C. | 发电机的线圈中产生的电动势最大值为$\frac{\sqrt{2}(R+r)}{R}$U | |
| D. | 从中性面开始计时,原线圈输入电压的瞬时值表达式为u=$\sqrt{2}$Usinωt |
16. 如图所示,相距为d的两条水平虚线Ll、L2之间是方向水平向里的匀强磁场,磁感应强度为B,正方形线圈abcd边长为L(L<d),质量为m,电阻为R,将线圈在磁场上方高h处静止释放,cd边刚进入磁场时速度为v0,cd边刚离开磁场时速度也为v0.则线圈穿越磁场的过程中,(从cd边刚进入磁场起一直到ab边离开磁场为止)以下说法正确的是( )
如图所示,相距为d的两条水平虚线Ll、L2之间是方向水平向里的匀强磁场,磁感应强度为B,正方形线圈abcd边长为L(L<d),质量为m,电阻为R,将线圈在磁场上方高h处静止释放,cd边刚进入磁场时速度为v0,cd边刚离开磁场时速度也为v0.则线圈穿越磁场的过程中,(从cd边刚进入磁场起一直到ab边离开磁场为止)以下说法正确的是( )
 如图所示,相距为d的两条水平虚线Ll、L2之间是方向水平向里的匀强磁场,磁感应强度为B,正方形线圈abcd边长为L(L<d),质量为m,电阻为R,将线圈在磁场上方高h处静止释放,cd边刚进入磁场时速度为v0,cd边刚离开磁场时速度也为v0.则线圈穿越磁场的过程中,(从cd边刚进入磁场起一直到ab边离开磁场为止)以下说法正确的是( )
如图所示,相距为d的两条水平虚线Ll、L2之间是方向水平向里的匀强磁场,磁感应强度为B,正方形线圈abcd边长为L(L<d),质量为m,电阻为R,将线圈在磁场上方高h处静止释放,cd边刚进入磁场时速度为v0,cd边刚离开磁场时速度也为v0.则线圈穿越磁场的过程中,(从cd边刚进入磁场起一直到ab边离开磁场为止)以下说法正确的是( )| A. | 感应电流所做的功为mgd | B. | 感应电流所做的功为2mgd | ||
| C. | 线圈的最小速度一定为$\frac{mgR}{{B}^{2}{L}^{2}}$ | D. | 线圈的最小速度一定为$\sqrt{2g(h+L-d)}$ |
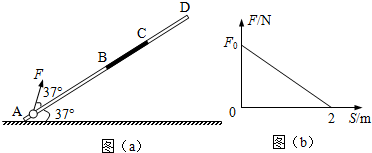 如图(a)所示,固定直杆AD与水平地面成37°角,长度分别为2m和1m的AB段和CD段光滑,长为1m的BC段粗糙.质量为1kg的小球套在直杆上,在方向与直杆成37°角的力F作用下,从杆底端A点处由静止开始运动,小球恰能到达顶端D点.已知力F与小球位移的大小关系如图(b)所示,球与BC段间的动摩擦因数为0.1,sin37°=0.6,cos37°=0.8,取g=10m/s2.求:
如图(a)所示,固定直杆AD与水平地面成37°角,长度分别为2m和1m的AB段和CD段光滑,长为1m的BC段粗糙.质量为1kg的小球套在直杆上,在方向与直杆成37°角的力F作用下,从杆底端A点处由静止开始运动,小球恰能到达顶端D点.已知力F与小球位移的大小关系如图(b)所示,球与BC段间的动摩擦因数为0.1,sin37°=0.6,cos37°=0.8,取g=10m/s2.求:
 如图所示,在容器A的顶部通过弹簧竖直悬挂小球B,小球B的质量为m,弹簧的劲度系数为k.现将小球从弹簧原长处静止释放,第一次运动到最低点的时间为t.则在任意的$\frac{t}{2}$时间内,小球下降的最大距离是$\frac{\sqrt{2}mg}{k}$,弹簧的弹性势能增加量最大值为$\frac{2{m}^{2}{g}^{2}}{k}$.
如图所示,在容器A的顶部通过弹簧竖直悬挂小球B,小球B的质量为m,弹簧的劲度系数为k.现将小球从弹簧原长处静止释放,第一次运动到最低点的时间为t.则在任意的$\frac{t}{2}$时间内,小球下降的最大距离是$\frac{\sqrt{2}mg}{k}$,弹簧的弹性势能增加量最大值为$\frac{2{m}^{2}{g}^{2}}{k}$.