题目内容
8.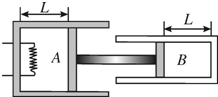 如图所示,绝热汽缸A与导热汽缸B均固定于地面,由刚性杆连接的绝热活塞与两汽缸间均无摩擦.已知两汽缸的横截面积之比SA:SB=2:1,两汽缸内均装有处于平衡状态的某理想气体,开始时两汽缸中的活塞与缸底的距离均为L,温度均为T0,压强均等于外界大气压.缓慢加热A中气体,停止加热达到稳定后,A中气体压强等于外界大气压的1.2倍.设环境温度始终保持不变,求
如图所示,绝热汽缸A与导热汽缸B均固定于地面,由刚性杆连接的绝热活塞与两汽缸间均无摩擦.已知两汽缸的横截面积之比SA:SB=2:1,两汽缸内均装有处于平衡状态的某理想气体,开始时两汽缸中的活塞与缸底的距离均为L,温度均为T0,压强均等于外界大气压.缓慢加热A中气体,停止加热达到稳定后,A中气体压强等于外界大气压的1.2倍.设环境温度始终保持不变,求(1)停止加热达到稳定后,A、B汽缸中的气体压强之比;
(2)稳定后汽缸A中活塞距缸底的距离.
分析 (1)中活塞在气体变化前后都是受力平衡,对活塞受力分析,利用力平衡可求得
(2)AB气体的变化中,B的变化是等温变化较简单,利用B的变化求得B变化后的LB,又因为AB两部分的总长度是定值,可解的A距底端的距离.
解答 解:(1)膨胀后A的压强
pA=1.2p0…①
加热后活塞平衡时,有:
(pA-p0)SA=(pB-p0)SB…②
则膨胀后B的压强为:
pB=1.4p0…③
由①~③式解得:
pA:pB=6:7
(2)设稳定后A、B两汽缸中活塞距缸底的距离分别为LA、LB,对B,有:
p0LSB=1.4p0LBSB…④
又:LA+LB=2L…⑤
由③④⑤式解得:
LA=$\frac{9}{7}$L
答:(1)停止加热达到稳定后,A、B汽缸中的气体压强之比为6:7;
(2)稳定后汽缸A中活塞距缸底的距离为$\frac{9}{7}L$.
点评 对连接体问题中,连接体在气体变化前后受力都平衡,所以对连接体利用受力平衡求解就很简单了,再者在两部分气体中,利用变化简单的气体,求解气体状态参量,会减少很多繁琐的过程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.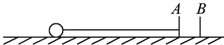 在光滑的水平面上相距40cm的两个钉子A和B,如图所示,长1m的细绳一端系着质量为0.4kg的小球,另一端固定在钉子A上,开始时,小球和钉子A、B在同一直线上,小球始终以2m/s的速率在水平面上做匀速圆周运动.若细绳能承受的最大拉力是4N,那么从开始到细绳断开所经历的时间是( )
在光滑的水平面上相距40cm的两个钉子A和B,如图所示,长1m的细绳一端系着质量为0.4kg的小球,另一端固定在钉子A上,开始时,小球和钉子A、B在同一直线上,小球始终以2m/s的速率在水平面上做匀速圆周运动.若细绳能承受的最大拉力是4N,那么从开始到细绳断开所经历的时间是( )
 在光滑的水平面上相距40cm的两个钉子A和B,如图所示,长1m的细绳一端系着质量为0.4kg的小球,另一端固定在钉子A上,开始时,小球和钉子A、B在同一直线上,小球始终以2m/s的速率在水平面上做匀速圆周运动.若细绳能承受的最大拉力是4N,那么从开始到细绳断开所经历的时间是( )
在光滑的水平面上相距40cm的两个钉子A和B,如图所示,长1m的细绳一端系着质量为0.4kg的小球,另一端固定在钉子A上,开始时,小球和钉子A、B在同一直线上,小球始终以2m/s的速率在水平面上做匀速圆周运动.若细绳能承受的最大拉力是4N,那么从开始到细绳断开所经历的时间是( )| A. | 0.8π s | B. | 0.9π s | C. | 1.2π s | D. | 1.6π s |
20. 如图所示,质量为m1=45kg的小船静止在湖面上,一质量为m2=50kg的人站在船头,向船尾方向水平抛出一质量为m0=5kg的小球,小球被抛出后相对小船的水平速度大小为v0=4m/s.则小球被抛出后相对湖面的水平速度大小为(空气和水的阻力忽略不计)( )
如图所示,质量为m1=45kg的小船静止在湖面上,一质量为m2=50kg的人站在船头,向船尾方向水平抛出一质量为m0=5kg的小球,小球被抛出后相对小船的水平速度大小为v0=4m/s.则小球被抛出后相对湖面的水平速度大小为(空气和水的阻力忽略不计)( )
 如图所示,质量为m1=45kg的小船静止在湖面上,一质量为m2=50kg的人站在船头,向船尾方向水平抛出一质量为m0=5kg的小球,小球被抛出后相对小船的水平速度大小为v0=4m/s.则小球被抛出后相对湖面的水平速度大小为(空气和水的阻力忽略不计)( )
如图所示,质量为m1=45kg的小船静止在湖面上,一质量为m2=50kg的人站在船头,向船尾方向水平抛出一质量为m0=5kg的小球,小球被抛出后相对小船的水平速度大小为v0=4m/s.则小球被抛出后相对湖面的水平速度大小为(空气和水的阻力忽略不计)( )| A. | 2.8m/s | B. | 3.2m/s | C. | 3.8m/s | D. | 4.2m/s |
17. 如图所示,在竖直平面内固定有两个很靠近的同心圆轨道,A、B分别为最高点和最低点(图中未标出),外圆光滑内圆粗糙.一质量为m=0.2kg的小球从轨道的最低点以水平向右的初速度v0开始运动,球的直径略小于两圆间距,球运动的轨道半径R=0.5m,重力加速度g取10m/s2,不计空气阻力,设小球过最低点B时重力势能为零,下列说法中正确的是( )
如图所示,在竖直平面内固定有两个很靠近的同心圆轨道,A、B分别为最高点和最低点(图中未标出),外圆光滑内圆粗糙.一质量为m=0.2kg的小球从轨道的最低点以水平向右的初速度v0开始运动,球的直径略小于两圆间距,球运动的轨道半径R=0.5m,重力加速度g取10m/s2,不计空气阻力,设小球过最低点B时重力势能为零,下列说法中正确的是( )
 如图所示,在竖直平面内固定有两个很靠近的同心圆轨道,A、B分别为最高点和最低点(图中未标出),外圆光滑内圆粗糙.一质量为m=0.2kg的小球从轨道的最低点以水平向右的初速度v0开始运动,球的直径略小于两圆间距,球运动的轨道半径R=0.5m,重力加速度g取10m/s2,不计空气阻力,设小球过最低点B时重力势能为零,下列说法中正确的是( )
如图所示,在竖直平面内固定有两个很靠近的同心圆轨道,A、B分别为最高点和最低点(图中未标出),外圆光滑内圆粗糙.一质量为m=0.2kg的小球从轨道的最低点以水平向右的初速度v0开始运动,球的直径略小于两圆间距,球运动的轨道半径R=0.5m,重力加速度g取10m/s2,不计空气阻力,设小球过最低点B时重力势能为零,下列说法中正确的是( )| A. | 若小球运动到最高点A时速度为0,则小球机械能一定不守恒 | |
| B. | 若小球第一次运动到最高点时速度大小为0,则v0一定等于2$\sqrt{5}$m/s | |
| C. | 若要小球不挤压内轨,则v0一定不小于5m/s | |
| D. | 若小球开始运动时初动能为1.6 J,则足够长时间后小球的机械能为1 J |
 如图所示,长为0.5m的细绳一端与一质量为1kg的小球(可看成质点)相连,可绕过O点的水平转轴在竖直面内无摩擦地转动.在最低点给一个5m/s的初速度,使小球恰好能通过最高点完成完整的圆周运动,g取10m/s2求:
如图所示,长为0.5m的细绳一端与一质量为1kg的小球(可看成质点)相连,可绕过O点的水平转轴在竖直面内无摩擦地转动.在最低点给一个5m/s的初速度,使小球恰好能通过最高点完成完整的圆周运动,g取10m/s2求: 如图所示,U形气缸固定在水平地面上,用重力不计的活塞封闭着一定质量的气体,已知气缸不漏气,活塞移动过程无摩擦.初始时,外界大气压强为p0,活塞紧压小挡板.现缓慢升高缸内气体的温度,则图中能反映气缸内气体的压强p随热力学温度T变化的图象是( )
如图所示,U形气缸固定在水平地面上,用重力不计的活塞封闭着一定质量的气体,已知气缸不漏气,活塞移动过程无摩擦.初始时,外界大气压强为p0,活塞紧压小挡板.现缓慢升高缸内气体的温度,则图中能反映气缸内气体的压强p随热力学温度T变化的图象是( )



 光滑水平面上放一带定滑轮的长方形木板A,木板A上的物体B用绕过定滑轮的轻绳与小球C相连,绕过定滑轮与B连接的轻绳是水平的,用一水平向左的拉力F作用在物体B上,恰使A、B、C保持相对静止,如图所示,已知A、B、C的质量均为m,重力加速度为g,求:
光滑水平面上放一带定滑轮的长方形木板A,木板A上的物体B用绕过定滑轮的轻绳与小球C相连,绕过定滑轮与B连接的轻绳是水平的,用一水平向左的拉力F作用在物体B上,恰使A、B、C保持相对静止,如图所示,已知A、B、C的质量均为m,重力加速度为g,求: 如图所示,在光滑的水平面上,一个质量为3m的小球A,以速度v跟质量为2m的静止的小球B发生碰撞.
如图所示,在光滑的水平面上,一个质量为3m的小球A,以速度v跟质量为2m的静止的小球B发生碰撞.