题目内容
18. 如图所示,在光滑的水平面上,一个质量为3m的小球A,以速度v跟质量为2m的静止的小球B发生碰撞.
如图所示,在光滑的水平面上,一个质量为3m的小球A,以速度v跟质量为2m的静止的小球B发生碰撞.(1)若A、B两球发生的是完全非弹性碰撞,求碰撞后小球B的速度?
(2)若A、B两球发生的是弹性碰撞,求碰撞后小球B的速度?
分析 (1)完全非弹性碰撞,碰撞后两小球粘在一起具有相同的速度根据动量守恒计算即可;
(2)发生弹性碰撞,没有能量的损失,同时动量也守恒,根据能量守恒和动量守恒看来计算速度的大小.
解答 解:(1)若为完全非弹性碰撞,碰撞后两小球粘在一起具有相同的速度
由动量守恒定律得:mAv=(mA+mB)v′
得$v′=\frac{3}{5}v$
(2)若为弹性碰撞,则碰撞前后两小球的总动能不变,则有
mAv=mAvA+mBvB
$\frac{1}{2}{m}_{A}{v}^{2}=\frac{1}{2}{m}_{A}{v}_{A}{\;}^{2}+\frac{1}{2}{m}_{B}{v}_{B}{\;}^{2}$
解得:${v}_{B}=\frac{6}{5}v$
答:(1)若A、B两球发生的是完全非弹性碰撞,碰撞后小球B的速度为$\frac{3}{5}v$;
(2)若A、B两球发生的是弹性碰撞,碰撞后小球B的速度为$\frac{6}{5}v$.
点评 本题考查的是动量定律得直接应用,注意动能是标量,速度是矢量,难度适中,属于中档题.

练习册系列答案
相关题目
9. 如图所示,物体A和B的质量均为m,且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦)在用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中,(0°<α<90°)则( )
如图所示,物体A和B的质量均为m,且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦)在用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中,(0°<α<90°)则( )
 如图所示,物体A和B的质量均为m,且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦)在用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中,(0°<α<90°)则( )
如图所示,物体A和B的质量均为m,且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦)在用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中,(0°<α<90°)则( )| A. | 物体A也做匀速直线运动 | B. | 物体A将竖直向上先加速后减速 | ||
| C. | 物体A将处于超重状态 | D. | 绳子对物体A的拉力保持不变 |
6.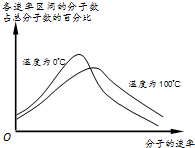 如图所示,是氧气在0℃和100℃两种不同情况下,各速率区间的分子数占总分子数的百分比与分子速率间的关系.由图可知( )
如图所示,是氧气在0℃和100℃两种不同情况下,各速率区间的分子数占总分子数的百分比与分子速率间的关系.由图可知( )
 如图所示,是氧气在0℃和100℃两种不同情况下,各速率区间的分子数占总分子数的百分比与分子速率间的关系.由图可知( )
如图所示,是氧气在0℃和100℃两种不同情况下,各速率区间的分子数占总分子数的百分比与分子速率间的关系.由图可知( )| A. | 100℃的氧气,速率大的分子比例较多 | |
| B. | 具有最大比例的速率区间,0℃时对应的速率大 | |
| C. | 温度越高,分子的平均速率越大 | |
| D. | 在0℃时,也有一部分分子的速率比较大,说明气体内部有温度较高的区域 |
3. 如图所示,在地面上以速度v0抛出质量为m的物体,抛出后物体落到比地面低h的海平面上.若以海平面为零势能面,不计空气阻力,则下列说法中正确的是( )
如图所示,在地面上以速度v0抛出质量为m的物体,抛出后物体落到比地面低h的海平面上.若以海平面为零势能面,不计空气阻力,则下列说法中正确的是( )
 如图所示,在地面上以速度v0抛出质量为m的物体,抛出后物体落到比地面低h的海平面上.若以海平面为零势能面,不计空气阻力,则下列说法中正确的是( )
如图所示,在地面上以速度v0抛出质量为m的物体,抛出后物体落到比地面低h的海平面上.若以海平面为零势能面,不计空气阻力,则下列说法中正确的是( )| A. | 物体到海平面时的重力势能为mgh | |
| B. | 重力对物体做的功为-mgh | |
| C. | 物体在海平面上的动能为$\frac{1}{2}$mv02+mgh | |
| D. | 物体在海平面上的机械能为$\frac{1}{2}$mv02 |
4.发电厂发电机的输出电压为U1,发电厂至用户的输电导线的总电阻为R,通过输电导线的电流为I,输电线末端的电压为U2,下面选项表示输电导线上损耗的功率不正确的是( )
| A. | $\frac{{U}_{1}^{2}}{R}$ | B. | $\frac{({U}_{1}-{U}_{2})^{2}}{R}$ | C. | I2R | D. | I(U1一U2) |
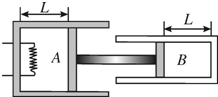 如图所示,绝热汽缸A与导热汽缸B均固定于地面,由刚性杆连接的绝热活塞与两汽缸间均无摩擦.已知两汽缸的横截面积之比SA:SB=2:1,两汽缸内均装有处于平衡状态的某理想气体,开始时两汽缸中的活塞与缸底的距离均为L,温度均为T0,压强均等于外界大气压.缓慢加热A中气体,停止加热达到稳定后,A中气体压强等于外界大气压的1.2倍.设环境温度始终保持不变,求
如图所示,绝热汽缸A与导热汽缸B均固定于地面,由刚性杆连接的绝热活塞与两汽缸间均无摩擦.已知两汽缸的横截面积之比SA:SB=2:1,两汽缸内均装有处于平衡状态的某理想气体,开始时两汽缸中的活塞与缸底的距离均为L,温度均为T0,压强均等于外界大气压.缓慢加热A中气体,停止加热达到稳定后,A中气体压强等于外界大气压的1.2倍.设环境温度始终保持不变,求 用油膜法估测分子的大小,方法及实验步骤如下:
用油膜法估测分子的大小,方法及实验步骤如下: