题目内容
9. 如图所示,一个质量为m=15kg的小号粮食麻袋,从离地面高h1=6m的天花板自由下落,一辆运粮平板车正沿着下落点正下方所在的平直路面以v0=6m/s的速度匀速前进.已知麻袋开始自由下落时,平板车前端恰好运动到距离下落点正下方s=3m处,该平板车总长L=7m,平板车板面离地面高h2=1m,麻袋可看做质点,不计空气阻力.假定麻袋落到板面后不弹起,在麻袋落到板面的瞬间,平板车开始以大小为a=4m/s2的加速度做匀减速直线运动,直至停止,g取10m/s2,麻袋与平板车板面间的动摩擦因数μ=0.2.求:
如图所示,一个质量为m=15kg的小号粮食麻袋,从离地面高h1=6m的天花板自由下落,一辆运粮平板车正沿着下落点正下方所在的平直路面以v0=6m/s的速度匀速前进.已知麻袋开始自由下落时,平板车前端恰好运动到距离下落点正下方s=3m处,该平板车总长L=7m,平板车板面离地面高h2=1m,麻袋可看做质点,不计空气阻力.假定麻袋落到板面后不弹起,在麻袋落到板面的瞬间,平板车开始以大小为a=4m/s2的加速度做匀减速直线运动,直至停止,g取10m/s2,麻袋与平板车板面间的动摩擦因数μ=0.2.求:(1)麻袋将落在平板车上距车左端多远处;
(2)通过计算说明,麻袋是否会滑到平板车的最左端;
(3)麻袋在平板车上相对滑动的过程中产生的总热量Q为多少.
分析 (1)麻袋做自由落体运动,根据下落高度求得时间,再位移公式求出此时间内平板车前进的距离,从而得到麻袋在车上的落点距车尾端距离;
(2)先由速度公式求出平板车和模型达到具有相同速度所用的时间,然后求出在这段时间内模型相对车向后的位移;
(3)麻袋在平板上来回摩擦产生的总热量:Q=μmg△x,△x是麻袋相对车向前的位移,由位移时间公式求解△x.
解答 解:(1)设麻袋经时间t1下落到平板车上,由运动学公式得:
h1-h2=$\frac{1}{2}$gt2 ①
平板车在t1时间内前进的距离为x1,则:x1=v0t1 ②
所以麻袋在平板车上的落点距车左端距离:s′=L+s-x1=4 m ③
(2)设麻袋落在车上后做匀加速运动的加速度为a1,经过时间t2麻袋和板车的速度相同为v,则:
板车的速度为:v=v0-at2 ④
麻袋的速度为:v=a1t2 ⑤
对麻袋应用牛顿第二定律得:μmg=ma1 ⑥
平板车的位移为:x2=v0t2-$\frac{1}{2}$at22;⑦
在这段时间内麻袋的位移为:x3=$\frac{1}{2}$a1t22 ⑧
联立④⑤⑥⑦⑧可得:
在这段时间内麻袋相对平板车向后的位移为:△x1=x2-x3=3 m ⑨
因△x1<4 m 故不会滑至平板车的左端⑩
(3)速度相同后麻袋和平板车各自做匀减速运动直到静止,
平板车的位移为:x4=$\frac{{v}^{2}}{2a}$⑪
麻袋的位移为:x5=$\frac{{v}^{2}}{2{a}_{1}}$⑫
麻袋相对车向前的位移为:△x2=x5-x4⑬
麻袋在平板车上来回摩擦产生的总热量:Q=μmg(△x1+△x2)=105 J⑭
答:
(1)麻袋将落在平板车上距车左端4 m.
(2)麻袋不会滑到最左端.
(3)麻袋在平板车上相对滑动的过程中产生的总热量Q为105 J.
点评 本题主要考查了自由落体运动、匀变速直线运动的基本公式的直接应用,关键要能正确分析平板车和麻袋的运动情况,并能把握它们之间的关系,如位移关系、速度关系.


| A. | Ff甲=Ff乙=Ff丙=μmg | B. | Ff甲=μmg,Ff乙<μmg,Ff丙>μmg | ||
| C. | Ff甲=μmg,Ff乙>μmg,Ff丙<μmg | D. | Ff甲=μmg,Ff乙<μmg,Ff丙<μmg |
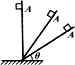 如图所示,让小物块由倾角为θ的光滑斜面上的A点由静止滑下,然后再逐渐增大θ角的条件下进行多次实验,下列说法正确的是( )
如图所示,让小物块由倾角为θ的光滑斜面上的A点由静止滑下,然后再逐渐增大θ角的条件下进行多次实验,下列说法正确的是( )| A. | 下落时间逐渐增大 | B. | 下落的加速度逐渐减小 | ||
| C. | 到达底端的动能不变 | D. | 重力做功的平均功率逐渐增大 |
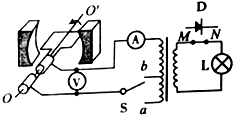 如图所示,一匝数为N=100的矩形线圈,面积S=0.01m2,内阻不计,绕垂直于磁感线的对称轴OO′匀速转动.设线圈经过的磁场为匀强磁场,磁感应强度B=2T.线圈通过-理想变压器后,接一标有“6V,3W”字样的灯泡L,变压器原线圈的总匝数为n1=200匝,b是原线圈的中心抽头,副线圈的匝数为n2=20匝.当开关S拨到b位置时,小灯泡恰好正常发光,设小灯泡的电阻不随温度发生变化,则( )
如图所示,一匝数为N=100的矩形线圈,面积S=0.01m2,内阻不计,绕垂直于磁感线的对称轴OO′匀速转动.设线圈经过的磁场为匀强磁场,磁感应强度B=2T.线圈通过-理想变压器后,接一标有“6V,3W”字样的灯泡L,变压器原线圈的总匝数为n1=200匝,b是原线圈的中心抽头,副线圈的匝数为n2=20匝.当开关S拨到b位置时,小灯泡恰好正常发光,设小灯泡的电阻不随温度发生变化,则( )| A. | 电路中电压表的读数为30$\sqrt{2}$V | |
| B. | 电路中电流表的读数$\frac{\sqrt{2}}{10}$A | |
| C. | 线圈转动的角速度15$\sqrt{2}$rad/s | |
| D. | 若将开关S拨到a位置.并将一个理想二极管D接到MN之间,其他条件不变,则此时线圈提供的功率为$\frac{3}{4}$W |
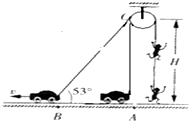 摄制组在某大楼边拍摄武打片,要求特技演员从地面飞到屋顶,如图所示.特技演员质量m=50kg,导演在离地H=12m处架设了定滑轮,轨道车从图中A位置以v=10m/s匀速前进到B位置时,绳BO与水平方向的夹角为53°,则轨道车从A位置运动到B位置的过程中(g取10m/s2,sin53°=0.8,cos53°=0.6)( )
摄制组在某大楼边拍摄武打片,要求特技演员从地面飞到屋顶,如图所示.特技演员质量m=50kg,导演在离地H=12m处架设了定滑轮,轨道车从图中A位置以v=10m/s匀速前进到B位置时,绳BO与水平方向的夹角为53°,则轨道车从A位置运动到B位置的过程中(g取10m/s2,sin53°=0.8,cos53°=0.6)( )| A. | 演员做匀速直线运动 | |
| B. | 演员最大速度为8m/s | |
| C. | 以地面为重力势能的零点,演员最大机械能为2400J | |
| D. | 钢丝绳在这一过程中对演员做功为900J |
 电荷量为+q,质量为m的小球处在竖直向下的匀强磁场中,电场强度大小为E,小球从高为H处静止球从高为H处静止开始释放,设小球在运动过程中始终受到大小恒定的空气阻力Ff的作用,与地面碰撞过程中小球没有能量和电量的损失,重力加速度为g,则( )
电荷量为+q,质量为m的小球处在竖直向下的匀强磁场中,电场强度大小为E,小球从高为H处静止球从高为H处静止开始释放,设小球在运动过程中始终受到大小恒定的空气阻力Ff的作用,与地面碰撞过程中小球没有能量和电量的损失,重力加速度为g,则( )| A. | 小球与地面第一次碰撞前的速度大小为$\sqrt{\frac{2(mg+qE+{F}_{f})H}{m}}$ | |
| B. | 小球与地面第一次碰撞前的加速度大小为$\frac{mg+qE}{m}$ | |
| C. | 小球从释放到最后静止,运动的总路程为$\frac{(mg+qE+{F}_{f})H}{mg+qE-{F}_{f}}$ | |
| D. | 小球从释放到最后静止,运动的总路程为$\frac{(mg+qE)H}{{F}_{f}}$ |
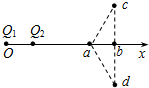 如图所示,真空中两个不等量的正点电荷Q1、Q2固定在x轴上,其中Q1>Q2.三角形acd为等腰三角形,cd边与x轴垂直且与x轴相交于b点,则下列说法正确的是( )
如图所示,真空中两个不等量的正点电荷Q1、Q2固定在x轴上,其中Q1>Q2.三角形acd为等腰三角形,cd边与x轴垂直且与x轴相交于b点,则下列说法正确的是( )| A. | a点场强小于b点场强 | |
| B. | c点电势等于b点电势 | |
| C. | c点电势等于d点电势 | |
| D. | 将电子从a点移到b点再移到c点电势能增加 |
 如图所示,一理想变压器的原、副线圈匝数之比为n1:n2=55:1,原线圈接入电压u=220$\sqrt{2}$sin100πt(V)的交流电源,图中电表均为理想电表,闭合开关后,当滑动变阻器的滑动触头P从最上端滑到最下端的过程中,下列说法正确的是( )
如图所示,一理想变压器的原、副线圈匝数之比为n1:n2=55:1,原线圈接入电压u=220$\sqrt{2}$sin100πt(V)的交流电源,图中电表均为理想电表,闭合开关后,当滑动变阻器的滑动触头P从最上端滑到最下端的过程中,下列说法正确的是( )| A. | 副线圈中交变电流的频率为100Hz | |
| B. | t=0.02s时,电压表的示数为0 | |
| C. | 电流表的示数先变小后变大 | |
| D. | 定值电阻R消耗的功率先变大后变小 |
| A. | 实现对接后,组合体运行速度大于第一宇宙速度 | |
| B. | 航天员景海鹏和陈冬能在天宫二号中自由飞翔,说明他们不受地球引力作用 | |
| C. | 如不加干预,在运行一段时间后,组合体的动能可能会增加 | |
| D. | 如不加干预,组合体的轨道高度将缓慢升高 |