题目内容
18.如图甲所示,一圆形线圈面积S=0.2m2,匝数N=10,电阻r=2Ω,与电路器P连接成闭合回路,电热器电阻R=3Ω,线圈处于磁感应强度周期性变化的匀强磁场中,当磁场磁感应强度按如图乙所示规律变化时,求:
(1)一分钟内电热器产生的热量;
(2)通过电热器电流的有效值.
分析 (1)根据法拉第电磁感应定律,结合闭合电路欧姆定律,及焦耳定律,求得一个周期内产生热量,进而可求得一分钟内电热器产生的热量;
(2)根据电流的热效应,运用焦耳定律,分段求得热量,结合交流电的有效值求法,从而即可求解.
解答 解:(1)根据法拉第电磁感应定律,则在0到0.2s内产生的感应电动势为E1=$N\frac{△B•S}{△t}$=10×$\frac{0.5}{0.2}$×0.2=5V;
由闭合电路欧姆定律,则有产生的电流I1=$\frac{{E}_{1}}{R+r}$=$\frac{5}{3+2}$=1A;
同理,在0.2s到0.3s内的产生的感应电动势为E2=$N\frac{△B′}{△t}S$=10×$\frac{0.5}{0.1}$×0.2=10V;
由闭合电路欧姆定律,则有产生的电流I2=$\frac{{E}_{2}}{R+r}$=$\frac{10}{3+2}$=2A;
那么一个周期内电热器产生热量Q0=${I}_{1}^{2}{Rt}_{1}{+I}_{2}^{2}R{t}_{2}$=12×3×0.2+22×3×0.1=1.8J
而一分钟内,共完成n=$\frac{60}{0.3}$=200个周期,
则一分钟内,电热器产生热量Q=$\frac{60}{0.3}×1.8$=360J;
(2)根据电流的热效应,设通过电热器电流的有效值为I,
则有:I2RT=${I}_{1}^{2}{Rt}_{1}{+I}_{2}^{2}R{t}_{2}$
解得:I=$\sqrt{2}$A;
答:(1)一分钟内电热器产生的热量360J;
(2)通过电热器电流的有效值$\sqrt{2}$A.
点评 考查法拉第电磁感应定律与闭合电路欧姆定律的应用,掌握焦耳定律的内容,注意求交流电的有效值的方法,是本题的关键.

 阅读快车系列答案
阅读快车系列答案
| A. | 甲物体的速度为450m/s | B. | 乙物体的加速度为20m/s2 | ||
| C. | 15s时,甲乙两物体相距150m | D. | 甲物体的速度比乙物体小 |
 如图所示,两根细线把两个相同的小球悬于同一点,并使两球在同一水平面内做匀速圆周运动,其中小球1的转动半径较大,则( )
如图所示,两根细线把两个相同的小球悬于同一点,并使两球在同一水平面内做匀速圆周运动,其中小球1的转动半径较大,则( )| A. | 两小球转动的加速速度大小关系为a1>a2 | |
| B. | 两小球转动的角速度大小关系为ω1=ω2 | |
| C. | 两小球转动的线速度大小关系为v1=v2 | |
| D. | 两根线中拉力大小关系为T1>T2 |

 一列沿x轴传播的间谐横波在t=0时刻的波的图象如图所示,经△t=0.1s,质点M第一次回到平衡位置,求:
一列沿x轴传播的间谐横波在t=0时刻的波的图象如图所示,经△t=0.1s,质点M第一次回到平衡位置,求: 某同学利用如图甲所示的电路测量一根细长陶瓷管表面导电膜的厚度,陶瓷管的厚度大于其表面涂有的导电膜的厚度.
某同学利用如图甲所示的电路测量一根细长陶瓷管表面导电膜的厚度,陶瓷管的厚度大于其表面涂有的导电膜的厚度.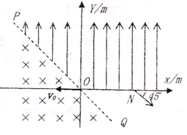 如图所示,在xoy平面内,直线PQ平分第二、四象限(即与y轴成45°),直线PQ左侧空间存在着垂直纸面向里的匀强磁场,PQ上侧且y>0空间存在着沿y轴正方向的匀强电场,场强大小为E=10V/m;一个比荷$\frac{q}{m}$=103C/kg的带负电的粒子(重力不计),从坐标原点O以v0=200m/s的速度沿着x轴负方向进入匀强磁场,粒子从O点入射后,最后从x轴上N点射出电场,方向恰好与x轴正方向成45°,求:
如图所示,在xoy平面内,直线PQ平分第二、四象限(即与y轴成45°),直线PQ左侧空间存在着垂直纸面向里的匀强磁场,PQ上侧且y>0空间存在着沿y轴正方向的匀强电场,场强大小为E=10V/m;一个比荷$\frac{q}{m}$=103C/kg的带负电的粒子(重力不计),从坐标原点O以v0=200m/s的速度沿着x轴负方向进入匀强磁场,粒子从O点入射后,最后从x轴上N点射出电场,方向恰好与x轴正方向成45°,求: 在“探究弹力和弹簧伸长关系”的实验中,某实验小组将不同数量的钩码分别挂在竖直弹簧下端,进行测量,根据实验所测数据,利用描点法作出了所挂钩码的重力G与弹簧总长L的关系图象,如图所示.根据图象回答以下问题.
在“探究弹力和弹簧伸长关系”的实验中,某实验小组将不同数量的钩码分别挂在竖直弹簧下端,进行测量,根据实验所测数据,利用描点法作出了所挂钩码的重力G与弹簧总长L的关系图象,如图所示.根据图象回答以下问题.