题目内容
16. 在风洞实验室中进行如图所示的实验.在倾角为37°的固定斜面上,有一个质量为0.5kg的物块,在风洞施加的水平恒力F作用下,从A点由静止开始运动,经过1.2s到达B点时立即关闭风洞,撤去恒力F,物块到达C点时速度变为零,通过速度传感器测得这一过程中物块每隔0.2s的瞬时速度,表格给出了部分数据:
在风洞实验室中进行如图所示的实验.在倾角为37°的固定斜面上,有一个质量为0.5kg的物块,在风洞施加的水平恒力F作用下,从A点由静止开始运动,经过1.2s到达B点时立即关闭风洞,撤去恒力F,物块到达C点时速度变为零,通过速度传感器测得这一过程中物块每隔0.2s的瞬时速度,表格给出了部分数据:| t/s | 0.0 | 0.2 | 0.4 | 0.6 | … | 1.4 | 1.6 | 1.8 | … |
| v/(m•s-1) | 0.0 | 1.0 | 2.0 | 3.0 | … | 4.0 | 2.0 | 0.0 | … |
(1)A、C两点间的距离;
(2)物块和斜面间的动摩擦因数μ;
(3)水平恒力F的大小.
分析 (1)由表格数据分别计算出加速过程和减速过程的加速度大小,并计算出关闭风洞时的速度大小,由运动学公式求出加速位移和减速位移,相加即为AC点距离.
(2)匀减速过程根据牛顿第二定律,列出关系式,求解动摩擦因数;
(3)匀加速过程根据牛顿第二定律求解可得出F大小.
解答 解:(1)物块匀加速运动过程中的加速度为:a1=
$\frac{△{v}_{1}}{△{t}_{1}}=\frac{3}{0.6}m/{s}^{2}$=5m/s2;
关闭风洞时的速度为:v=a1t=5×1.2m/s=6m/s
关闭风洞后物块匀减速运动的加速度为:a2=$\frac{△{v}_{2}}{△{t}_{2}}$=$\frac{-4}{0.4}m/{s}^{2}$=-10m/s2,
匀加速过程的位移:x1=$\frac{1}{2}{a}_{1}{t}^{2}=\frac{1}{2}×5×1.{2}^{2}m=3.6m$;
匀减速过程的位移:x2=$-\frac{({a}_{1}{t}_{1})^{2}}{2{a}_{2}}=\frac{36}{20}$m=1.8m
故A、C两点间的距离为:x=x1+x2=3.6m+1.8m=5.4m;
(2)根据牛顿第二定律可得:
匀减速过程:-(mgsin37°+μmgcos37°)=ma2,
解得:μ=0.5;
(3)匀加速过程:Fcos37°-mgsin37°-(mgcos37°+Fsin37°)=ma1,
解得:F=15N.
答:(1)A、C两点间的距离5.4m;
(2)物块和斜面间的动摩擦因数为0.5;
(3)水平恒力F的大小为15N.
点评 对于牛顿第二定律的综合应用问题,关键是弄清楚物体的运动过程和受力情况,利用牛顿第二定律或运动学的计算公式求解加速度,再根据题目要求进行解答;知道加速度是联系静力学和运动学的桥梁.

 如图所示,一带电小球用绝缘丝线悬挂在很大的水平方向匀强电场中,当小球静止后把丝线烧断,则小球在电场中将( )
如图所示,一带电小球用绝缘丝线悬挂在很大的水平方向匀强电场中,当小球静止后把丝线烧断,则小球在电场中将( )| A. | 做自由落体运动 | B. | 做平抛运动 | ||
| C. | 沿悬线延长线做匀加速直线运动 | D. | 做变加速直线运动 |
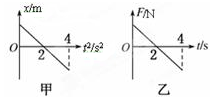 物体甲、乙原来静止于光滑水平面上.从t=0时刻开始,甲沿水平面做直线运动,位移x和时间平方t2的关系图象如图甲;乙受到如图乙所示的水平拉力F的作用.则在0~4s的时间内( )
物体甲、乙原来静止于光滑水平面上.从t=0时刻开始,甲沿水平面做直线运动,位移x和时间平方t2的关系图象如图甲;乙受到如图乙所示的水平拉力F的作用.则在0~4s的时间内( )| A. | 甲物体所受合力不断变化 | B. | 2s末乙物体速度达到最大 | ||
| C. | 2s末乙物体速度为0 | D. | 2s末乙物体改变运动方向 | ||
| E. | 甲物体的速度不断减小 |

| A. | 木板的速度大小为2m/s | |
| B. | 3s~4.5s时间内,物体B的加速度大小为2m/s2 | |
| C. | AB间的动摩擦因数为0.2 | |
| D. | 0~2s为保持木板做匀速运动,需施加一个水平向右大小为3N的力 |
 如图所示,一质点初速度大小不变,在O点受竖直面内一恒力作用.若初速度向右,其在竖直面上的运动轨迹如曲线甲,若初速度向左,其在竖直面上的运动轨迹如曲线乙;P、Q分别为甲乙轨迹上等高的点.则下列说法正确的是( )
如图所示,一质点初速度大小不变,在O点受竖直面内一恒力作用.若初速度向右,其在竖直面上的运动轨迹如曲线甲,若初速度向左,其在竖直面上的运动轨迹如曲线乙;P、Q分别为甲乙轨迹上等高的点.则下列说法正确的是( )| A. | 质点在P点的速度大 | B. | 质点在Q点的速度大 | ||
| C. | 质点在P点的加速度大 | D. | 质点在Q点的加速度大 |
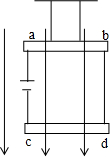 如图所示,ab、cd是两个长度均为L=4m,质量分别为m1=0.6kg和m2=0.2kg的金属棒,两根等长的细金属丝与一电动势为12V的电池相连,电路总电阻为24Ω.电池与两个金属棒串联成闭合回路,整个回路用绝缘细线悬挂在天花板呢上,且保证两金属棒水平.整个装置处于竖直向下的匀强磁场中,磁感应强度大小B=1T,特系统稳定之后(细金属丝和电池的质量不计,g=10m/s2),求:
如图所示,ab、cd是两个长度均为L=4m,质量分别为m1=0.6kg和m2=0.2kg的金属棒,两根等长的细金属丝与一电动势为12V的电池相连,电路总电阻为24Ω.电池与两个金属棒串联成闭合回路,整个回路用绝缘细线悬挂在天花板呢上,且保证两金属棒水平.整个装置处于竖直向下的匀强磁场中,磁感应强度大小B=1T,特系统稳定之后(细金属丝和电池的质量不计,g=10m/s2),求: 如图所示,足够长的传送带与水平面夹角为θ,以大小为v0的速度顺时针匀速转动,在传送带的上端放置一个小木块,并使小木块以大小为2v0的初速度沿传送带向下运动,小木块与传送带间的动摩擦因数μ>tanθ,下面四幅图能客观地反映小木块的速度随时间变化关系的是(以木块的初速度方向为正方向)( )
如图所示,足够长的传送带与水平面夹角为θ,以大小为v0的速度顺时针匀速转动,在传送带的上端放置一个小木块,并使小木块以大小为2v0的初速度沿传送带向下运动,小木块与传送带间的动摩擦因数μ>tanθ,下面四幅图能客观地反映小木块的速度随时间变化关系的是(以木块的初速度方向为正方向)( )



 某次对新能源汽车性能进行的测量中,汽车在水平测试平台上由静止开始沿直线运动,汽车所受动力随时间变化关系如图1所示,而速度传感器只传回第10s以后的数据(如图2所示).已知汽车质量为1000kg,汽车所受阻力恒定.求:
某次对新能源汽车性能进行的测量中,汽车在水平测试平台上由静止开始沿直线运动,汽车所受动力随时间变化关系如图1所示,而速度传感器只传回第10s以后的数据(如图2所示).已知汽车质量为1000kg,汽车所受阻力恒定.求: