题目内容
6.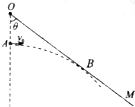 如图所示,挡板OM与竖直方向所夹的锐角为θ,一小球(视为质点)从O点正下方和A点以速度v0水平抛出,小球运动过程中恰好不和挡板碰撞(小球轨迹所在平面与挡板垂直).不计空气阻力,重力加速度大小为g,求:
如图所示,挡板OM与竖直方向所夹的锐角为θ,一小球(视为质点)从O点正下方和A点以速度v0水平抛出,小球运动过程中恰好不和挡板碰撞(小球轨迹所在平面与挡板垂直).不计空气阻力,重力加速度大小为g,求:(1)小球恰好不和挡板碰撞时的竖直速度大小;
(2)O、A间的距离.
分析 (1)根据小球恰好不和挡板碰撞,达到斜面时,速度方向与斜面恰好平行,结合平行四边形定则求出竖直分速度的大小.
(2)根据速度的关系求出平抛运动的时间,从而求出平抛运动的水平位移和竖直位移,结合几何关系求出OA间的距离.
解答 解:(1)由于小球恰好不和挡板碰撞,达到斜面时,速度方向与斜面恰好平行,有:cotθ=$\frac{{v}_{y}}{{v}_{0}}$,
解得vy=v0cotθ.
(2)根据cotθ=$\frac{gt}{{v}_{0}}$得运动的时间为:t=$\frac{{v}_{0}cotθ}{g}$,
根据x=v0t,y=$\frac{1}{2}g{t}^{2}$得解得平抛运动的水平位移为:x=$\frac{{{v}_{0}}^{2}cotθ}{g}$,竖直位移为:y=$\frac{{{v}_{0}}^{2}co{t}^{2}θ}{2g}$,
由几何关系得:$\frac{h+y}{x}=cotθ$,
联立解得:h=$\frac{{{v}_{0}}^{2}co{t}^{2}θ}{2g}$.
答:(1)小球恰好不和挡板碰撞时的竖直速度大小为v0cotθ;
(2)O、A间的距离为$\frac{{{v}_{0}}^{2}co{t}^{2}θ}{2g}$.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式和几何关系综合求解,难度中等.

练习册系列答案
相关题目
16. 在如图所示的电路中,电源两端的电压恒定,D为发光二极管(电流越大,发出的光越强),R0为定值电阻,R为光敏电阻(D发出的光越强,R的阻值越小),下列说法正确的是( )
在如图所示的电路中,电源两端的电压恒定,D为发光二极管(电流越大,发出的光越强),R0为定值电阻,R为光敏电阻(D发出的光越强,R的阻值越小),下列说法正确的是( )
 在如图所示的电路中,电源两端的电压恒定,D为发光二极管(电流越大,发出的光越强),R0为定值电阻,R为光敏电阻(D发出的光越强,R的阻值越小),下列说法正确的是( )
在如图所示的电路中,电源两端的电压恒定,D为发光二极管(电流越大,发出的光越强),R0为定值电阻,R为光敏电阻(D发出的光越强,R的阻值越小),下列说法正确的是( )| A. | 当滑动触头P向左移动时,R0消耗的功率增大 | |
| B. | 当滑动触头P向左移动时,R0消耗的功率减少 | |
| C. | 当滑动触头P向左移动时,R0消耗的功率可能不变 | |
| D. | 无论怎样移动滑动触头P,R0消耗的功率都不变 |
17.如图甲所示,物体受到水平推力F的作用,在粗糙水平面上做直线运动.通过力传感器和速度传感器监测到推力F和物体速度v随时间t变化的规律如图乙所示.重力加速度g=10m/s2.则( )
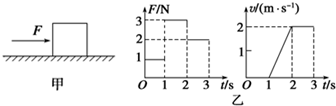

| A. | 物体的质量m=0.5kg | |
| B. | 物体与水平面间的动摩擦因数μ=0.2 | |
| C. | 第2s内物体克服摩擦力做的功W=2J | |
| D. | 前2s内推力F做功的平均功率$\overline{P}$=1.5W |
11. 伽利略对落体运动的研究,是科学实验和逻辑思维的完美结合,如图所示可大致表示其实验和思维的过程,对这一过程的分析,正确的是( )
伽利略对落体运动的研究,是科学实验和逻辑思维的完美结合,如图所示可大致表示其实验和思维的过程,对这一过程的分析,正确的是( )
 伽利略对落体运动的研究,是科学实验和逻辑思维的完美结合,如图所示可大致表示其实验和思维的过程,对这一过程的分析,正确的是( )
伽利略对落体运动的研究,是科学实验和逻辑思维的完美结合,如图所示可大致表示其实验和思维的过程,对这一过程的分析,正确的是( )| A. | 其中的甲图是实验现象,丁图是经过合理的外推得到的结论 | |
| B. | 其中的丁图是实验现象,甲图是经过合理的外推得到的结论 | |
| C. | 运用甲图的实验,可“冲淡”重力的作用,使实验现象更明显 | |
| D. | 运用丁图的实验,可“冲淡”重力的作用,使实验现象更明显 |
17.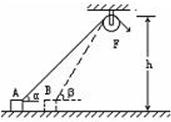 如图所示,用恒力F通过光滑的定滑轮,将静止于水平面上的物体从位置A拉到位置B,物体可视为质点,定滑轮距水平面高为h,物体在位置A、B时,细绳与水平面的夹角分别为α和β,从A到B绳的拉力F对物体做的功为( )
如图所示,用恒力F通过光滑的定滑轮,将静止于水平面上的物体从位置A拉到位置B,物体可视为质点,定滑轮距水平面高为h,物体在位置A、B时,细绳与水平面的夹角分别为α和β,从A到B绳的拉力F对物体做的功为( )
 如图所示,用恒力F通过光滑的定滑轮,将静止于水平面上的物体从位置A拉到位置B,物体可视为质点,定滑轮距水平面高为h,物体在位置A、B时,细绳与水平面的夹角分别为α和β,从A到B绳的拉力F对物体做的功为( )
如图所示,用恒力F通过光滑的定滑轮,将静止于水平面上的物体从位置A拉到位置B,物体可视为质点,定滑轮距水平面高为h,物体在位置A、B时,细绳与水平面的夹角分别为α和β,从A到B绳的拉力F对物体做的功为( )| A. | Fh($\frac{1}{tanα}$-$\frac{1}{tanβ}$) | B. | Fh($\frac{1}{sinα}$-$\frac{1}{sinβ}$) | C. | Fh($\frac{1}{cosα}$-$\frac{1}{cosβ}$) | D. | Fh($\frac{1}{cosβ}$-$\frac{1}{cosα}$) |
18.下列有关原子结构和原子核的说法中正确的是( )
| A. | 玻尔理论能很好地解释氢原子光谱 | |
| B. | 某元素的原子核半衰期为4天,则100个该元素的原子核8天后还剩25个 | |
| C. | β射线是高速电子流,证明该射线来自于核外 | |
| D. | 铀核发生裂变后,生成的新核的比结合能比铀核小 |




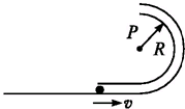 如图所示,半径为R,内径很小的光滑半圆管道竖直放置,质量为m的小球以某一速度进入管内,小球通过最高点P时,对管壁的压力为0,已知重力加速度为g.求:
如图所示,半径为R,内径很小的光滑半圆管道竖直放置,质量为m的小球以某一速度进入管内,小球通过最高点P时,对管壁的压力为0,已知重力加速度为g.求: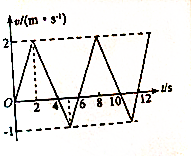 质量为1kg的物体,在周期性水平外力作用下,由静止开始在光滑水平面上运动,物体的速度随时间变化的图线(部分)如图所示,求:
质量为1kg的物体,在周期性水平外力作用下,由静止开始在光滑水平面上运动,物体的速度随时间变化的图线(部分)如图所示,求: