题目内容
17.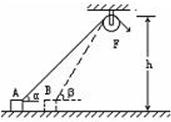 如图所示,用恒力F通过光滑的定滑轮,将静止于水平面上的物体从位置A拉到位置B,物体可视为质点,定滑轮距水平面高为h,物体在位置A、B时,细绳与水平面的夹角分别为α和β,从A到B绳的拉力F对物体做的功为( )
如图所示,用恒力F通过光滑的定滑轮,将静止于水平面上的物体从位置A拉到位置B,物体可视为质点,定滑轮距水平面高为h,物体在位置A、B时,细绳与水平面的夹角分别为α和β,从A到B绳的拉力F对物体做的功为( )| A. | Fh($\frac{1}{tanα}$-$\frac{1}{tanβ}$) | B. | Fh($\frac{1}{sinα}$-$\frac{1}{sinβ}$) | C. | Fh($\frac{1}{cosα}$-$\frac{1}{cosβ}$) | D. | Fh($\frac{1}{cosβ}$-$\frac{1}{cosα}$) |
分析 对绳头分析,根据几何知识求出绳端点的位移大小x,由公式W=Fx求解绳的拉力F对物体做的功.
解答 解:根据几何知识可知,绳端点的位移大小为:
x=$\frac{h}{sinα}$-$\frac{h}{sinβ}$
绳的拉力F对物体做的功为:
W=Fx=Fh($\frac{1}{sinα}$-$\frac{1}{sinβ}$).
故选:B.
点评 本题要善于将变力的功转化为恒力的功来求解:绳对物体的拉力大小不变,而方向改变是变力,但从绳的端点看拉力是恒力,功可以直接由功的公式计算.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
5.质量为5t的汽车,在水平公路上由静止开始做匀加速直线运动,加速度为2m/s2,所受阻力是1000N,则汽车第1s末的功率是( )
| A. | 22 KW | B. | 20 KW | C. | 11 KW | D. | 2 KW |
5. 细绳栓一个质量为m的小球,小球用固定在墙上的水平轻质弹簧支撑,小球与弹簧不粘连,平衡时细绳与竖直方向的夹角为53°,如图所示.(已知cos53°=0.6,sin53°=0.8)以下说法正确的是( )
细绳栓一个质量为m的小球,小球用固定在墙上的水平轻质弹簧支撑,小球与弹簧不粘连,平衡时细绳与竖直方向的夹角为53°,如图所示.(已知cos53°=0.6,sin53°=0.8)以下说法正确的是( )
 细绳栓一个质量为m的小球,小球用固定在墙上的水平轻质弹簧支撑,小球与弹簧不粘连,平衡时细绳与竖直方向的夹角为53°,如图所示.(已知cos53°=0.6,sin53°=0.8)以下说法正确的是( )
细绳栓一个质量为m的小球,小球用固定在墙上的水平轻质弹簧支撑,小球与弹簧不粘连,平衡时细绳与竖直方向的夹角为53°,如图所示.(已知cos53°=0.6,sin53°=0.8)以下说法正确的是( )| A. | 小球静止时弹簧的弹力大小为$\frac{3}{5}$mg | |
| B. | 小球静止时细绳的拉力大小为$\frac{3}{5}$mg | |
| C. | 将弹簧瞬间撤掉小球的加速度立即为$\frac{4}{3}$g | |
| D. | 细线烧断瞬间小球的加速度立即为$\frac{5}{3}$g |
12.如图所示,a、b、c、d四个图是不同的单色光形成的双缝干涉或单缝衍射图样.分析各图样的特点可以得出的正确结论是( )


| A. | a、b是光的干涉图样 | |
| B. | c、d是光的干涉图样 | |
| C. | 形成a图样光的波长比形成b图样光的波长短 | |
| D. | c、d中央条纹为暗纹 |
2. 如图所示,将一轻弹簧下端固定在倾角为θ的粗糙斜面底端,弹簧处于自然状态时上端位于A点,质量为m的物体从斜面上的B点由静止下滑,与弹簧发生相互作用后,最终停在斜面上,斜面始终静止,下列说法中正确的是( )
如图所示,将一轻弹簧下端固定在倾角为θ的粗糙斜面底端,弹簧处于自然状态时上端位于A点,质量为m的物体从斜面上的B点由静止下滑,与弹簧发生相互作用后,最终停在斜面上,斜面始终静止,下列说法中正确的是( )
 如图所示,将一轻弹簧下端固定在倾角为θ的粗糙斜面底端,弹簧处于自然状态时上端位于A点,质量为m的物体从斜面上的B点由静止下滑,与弹簧发生相互作用后,最终停在斜面上,斜面始终静止,下列说法中正确的是( )
如图所示,将一轻弹簧下端固定在倾角为θ的粗糙斜面底端,弹簧处于自然状态时上端位于A点,质量为m的物体从斜面上的B点由静止下滑,与弹簧发生相互作用后,最终停在斜面上,斜面始终静止,下列说法中正确的是( )| A. | 物体第一次反弹后不可能达到B点 | |
| B. | 物体最终将停在A、B之间的某处 | |
| C. | 整个过程中物体重力势能的减少量等于克服摩擦力做的功 | |
| D. | 物块与弹簧组成的系统的机械能减少 |
9.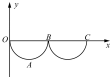 如图所示,xOy坐标平面在竖直面内,y轴正方向竖直向上,空间有垂直于xOy平面的匀强磁场(图中未画出).一带电小球从O点由静止释放,运动轨迹如图中曲线所示,下列说法正确有是( )
如图所示,xOy坐标平面在竖直面内,y轴正方向竖直向上,空间有垂直于xOy平面的匀强磁场(图中未画出).一带电小球从O点由静止释放,运动轨迹如图中曲线所示,下列说法正确有是( )
 如图所示,xOy坐标平面在竖直面内,y轴正方向竖直向上,空间有垂直于xOy平面的匀强磁场(图中未画出).一带电小球从O点由静止释放,运动轨迹如图中曲线所示,下列说法正确有是( )
如图所示,xOy坐标平面在竖直面内,y轴正方向竖直向上,空间有垂直于xOy平面的匀强磁场(图中未画出).一带电小球从O点由静止释放,运动轨迹如图中曲线所示,下列说法正确有是( )| A. | 洛伦兹力可能做了功 | |
| B. | 小球在整个运动过程中机械能增加 | |
| C. | 小球在A点时受到的洛伦兹力与重力大小相等 | |
| D. | 小球运动至最低点A时速度最大,且沿水平方向 |
6.质量分别为mA=1.0kg和mB=2.0kg的两小球A和B,原来在光滑水平面上沿同一直线、相同方向运动,速度分别为vA=6.0m/s、vB=2.0m/s.当A追上B时两小球发生正碰,则碰撞结束之后两小球A、B速度的可能是( )
| A. | vA′=5.0m/s,vB′=2.5m/s | B. | vA′=2.0m/s,vB′=4.0m/s | ||
| C. | vA′=3.0m/s,vB′=3.5m/s | D. | vA′=-2.0m/s,vB′=6.0m/s |
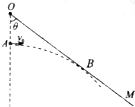 如图所示,挡板OM与竖直方向所夹的锐角为θ,一小球(视为质点)从O点正下方和A点以速度v0水平抛出,小球运动过程中恰好不和挡板碰撞(小球轨迹所在平面与挡板垂直).不计空气阻力,重力加速度大小为g,求:
如图所示,挡板OM与竖直方向所夹的锐角为θ,一小球(视为质点)从O点正下方和A点以速度v0水平抛出,小球运动过程中恰好不和挡板碰撞(小球轨迹所在平面与挡板垂直).不计空气阻力,重力加速度大小为g,求: 如图所示,在光滑水平面上,有足够长度的木板B,质量为mB=4kg,其上有一滑块C,质量为mC=4kg,B、C之间的动摩擦因数为0.2.现有质量为mA=lkg的滑块A,以v0=12m/s的初速度向B运动,与B碰撞(碰撞时间极短)后以4m/s速度弹回.求:
如图所示,在光滑水平面上,有足够长度的木板B,质量为mB=4kg,其上有一滑块C,质量为mC=4kg,B、C之间的动摩擦因数为0.2.现有质量为mA=lkg的滑块A,以v0=12m/s的初速度向B运动,与B碰撞(碰撞时间极短)后以4m/s速度弹回.求: