题目内容
6.“嫦娥一号”成功实现了绕月飞行,已知月球表面的重力加速度是地球重力加速度的$\frac{1}{6}$,月球半径是地球半径的$\frac{1}{4}$,则月球密度与地球密度之比以及月球第一宇宙速度与地球第一宇宙速度之比分别是( )| A. | $\frac{1}{2}$和$\frac{1}{24}$ | B. | $\frac{\sqrt{2}}{2}$和$\frac{\sqrt{6}}{12}$ | C. | $\frac{2}{3}$和$\frac{1}{12}$ | D. | $\frac{2}{3}$和$\frac{\sqrt{6}}{12}$ |
分析 在天体表面$G\frac{Mm}{{R}^{2}}=mg$,根据密度定义表示出密度公式,再通过已知量进行比较.
根据万有引力提供向心力,列出等式表示出周期和第一宇宙速度,再通过已知量进行比较.
解答 解:在天体表面$G\frac{Mm}{{R}^{2}}=mg$,所以GM=gR2,已知月球表面的重力加速度是地球重力加速度的$\frac{1}{6}$,月球半径是地球半径的$\frac{1}{4}$,所以地球的质量与月球的质量之间的关系为:
$\frac{{M}_{地}}{{M}_{月}}=\frac{{g}_{地}}{{g}_{月}}•{(\frac{{R}_{地}}{{R}_{月}})}^{2}$
根据:ρ=$\frac{M}{V}$=$\frac{M}{\frac{4}{3}π{R}^{3}}$,GM=gR2,所以ρ=$\frac{3g}{4πR}$
地球的平均密度与月球的平均密度之比为:$\frac{{ρ}_{月}}{{ρ}_{地}}=\frac{{g}_{月}}{{g}_{地}}•\frac{{R}_{地}}{{R}_{月}}=\frac{1}{6}×\frac{4}{1}=\frac{2}{3}$;
忽略地球的自转则有万有引力等于物体的重力,当卫星贴近地球表面圆周运动运动时有:
mg地=m$\frac{{v}_{1}^{2}}{{R}_{地}}$
解得:v1=$\sqrt{{g}_{地}{R}_{地}}$
同理当登月舱在月球表面作圆周运动时,有:
mg月=m$\frac{{v}_{2}^{2}}{{R}_{月}}$
解得:v2=$\sqrt{{g}_{月}{R}_{月}}$
故$\frac{{v}_{2}}{{v}_{1}}$=$\sqrt{\frac{{g}_{月}{R}_{月}}{{g}_{地}{R}_{地}}}$=$\sqrt{\frac{1}{4}×\frac{1}{6}}$=$\frac{\sqrt{6}}{12}$;
所以选项D正确,ABC错误.
故选:D
点评 求一个物理量之比,我们应该把这个物理量先用已知的物理量表示出来,再进行之比.
当不知道中心天体的质量和万有引力常量G,并知道中心天体表面的重力加速度g的时候要用黄金代换公式G$\frac{Mm}{{r}^{2}}$=mg求出GM=gr2.这是我们常用的一个技巧和方法要注意掌握.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案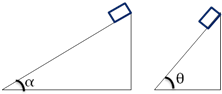 如图所示,两个质量相同的物体从同一高度沿倾角不同的两个光滑斜面由静止滑下,到达斜面底端的过程中,两物体相同的物理量为( )
如图所示,两个质量相同的物体从同一高度沿倾角不同的两个光滑斜面由静止滑下,到达斜面底端的过程中,两物体相同的物理量为( )| A. | 重力的冲量 | B. | 弹力的冲量 | ||
| C. | 合外力的冲量 | D. | 动量改变量的大小 |
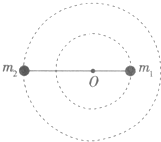 经长期观测,人们在宇宙中已经发现了“双星系统”,“双星系统”由两颗相距较近的恒星组成,每个恒星的线度远小于两个星体之间的距离,而且双星系统一般远离其他天体.如图所示,两颗星球组成的双星,在相互之间的万有引力作用下,绕连线上的0点做周期相同的匀速圆周运动. 现测得两颗星之间的距离为L,质量之比为m1:m2=3:2.则可知( )
经长期观测,人们在宇宙中已经发现了“双星系统”,“双星系统”由两颗相距较近的恒星组成,每个恒星的线度远小于两个星体之间的距离,而且双星系统一般远离其他天体.如图所示,两颗星球组成的双星,在相互之间的万有引力作用下,绕连线上的0点做周期相同的匀速圆周运动. 现测得两颗星之间的距离为L,质量之比为m1:m2=3:2.则可知( )| A. | m1、m2做圆周运动的线速度之比为3:2 | |
| B. | m1做圆周运动的半径为$\frac{2L}{5}$ | |
| C. | m1、m2做圆周运动的向心力大小相等 | |
| D. | m1、m2做圆周运动的周期的平方与m1 和 m2+的质量之和成反比 |
| A. | 小船渡河的最短时间为6s | |
| B. | 小船渡河的最短时间为10s | |
| C. | 小船渡河的最短时间为8s | |
| D. | 小船渡河时间最短时船头指向不能确定 |
| A. | 100V,1次 | B. | 100V,2次 | C. | 141V,1次 | D. | 141V,2次 |
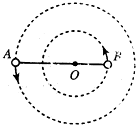 神奇的黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其他天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示.引力常量为G,由观测能够得到可见星A的速率v和运行周期T.
神奇的黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其他天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示.引力常量为G,由观测能够得到可见星A的速率v和运行周期T.