题目内容
12. 如图所示,放置在竖直平面内的$\frac{1}{4}$圆轨道AB,O点为圆心,OA水平,OB竖直,半径为2$\sqrt{2}$m.在O点沿OA抛出一小球,小球击中圆弧AB上的中点C,vt的反向延长线与OB的延长线相交于D点.已知重力加速度g=10m/s2.求:
如图所示,放置在竖直平面内的$\frac{1}{4}$圆轨道AB,O点为圆心,OA水平,OB竖直,半径为2$\sqrt{2}$m.在O点沿OA抛出一小球,小球击中圆弧AB上的中点C,vt的反向延长线与OB的延长线相交于D点.已知重力加速度g=10m/s2.求:(1)小球运动的时间?
(2)OD的长度为多少?
分析 小球击中圆弧AB上的中点C,得出平抛运动的水平位移和竖直位移,根据竖直方向做自由落体运动求出平抛运动的时间.平抛运动速度的反向延长线经过其水平位移的中点.求出C点的速度方向,根据几何关系求出h.
解答 解:(1)平抛运动的水平位移和竖直位移相等,x=y=Rcos45°=2m
根据y=$\frac{1}{2}g{t}^{2}$
得,t=$\sqrt{\frac{2y}{g}}$=$\sqrt{\frac{2}{5}}$s
(2)设OA与速度的反向延长线的交点为E,因为平抛运动速度的反向延长线经过其水平位移的中点,则OE=1m
设速度与水平方向的夹角为θ,因为速度与水平方向夹角的正切值等于此时位移与水平方向夹角正切值的两倍.
则tanθ=2tan45°=2
设角BDC为α,则tanα=$\frac{OE}{h}=\frac{1}{ttanθ}=\frac{1}{2}$
所以h=2m
答:(1)小球运动的时间是$\sqrt{\frac{2}{5}}$s;
(2)OD的长度为2m.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,以及掌握平抛运动的推论,某时刻速度与水平方向夹角的正切值等于此时位移与水平方向夹角正切值的两倍.

练习册系列答案
相关题目
2. 如图,某滑雪运动员从高处平台边A点以初速度v0水平飞出,恰好落在斜边底部B点.已知高AC=3.2m,水平距离BC=8m,取g=10m/s2,则运动员在空中运动的时间t及水平初速度v0分别为( )
如图,某滑雪运动员从高处平台边A点以初速度v0水平飞出,恰好落在斜边底部B点.已知高AC=3.2m,水平距离BC=8m,取g=10m/s2,则运动员在空中运动的时间t及水平初速度v0分别为( )
 如图,某滑雪运动员从高处平台边A点以初速度v0水平飞出,恰好落在斜边底部B点.已知高AC=3.2m,水平距离BC=8m,取g=10m/s2,则运动员在空中运动的时间t及水平初速度v0分别为( )
如图,某滑雪运动员从高处平台边A点以初速度v0水平飞出,恰好落在斜边底部B点.已知高AC=3.2m,水平距离BC=8m,取g=10m/s2,则运动员在空中运动的时间t及水平初速度v0分别为( )| A. | t=0.8s | B. | t=1.0s | C. | v0=8m/s | D. | v0=10m/s |
3. 如图所示,小球的质量为m,自光滑的斜槽的顶端A无处速滑下,沿虚线轨迹落地,不计空气阻力,则小球着地瞬间的重力势能是(选取O点所在平面为参考平面)( )
如图所示,小球的质量为m,自光滑的斜槽的顶端A无处速滑下,沿虚线轨迹落地,不计空气阻力,则小球着地瞬间的重力势能是(选取O点所在平面为参考平面)( )
 如图所示,小球的质量为m,自光滑的斜槽的顶端A无处速滑下,沿虚线轨迹落地,不计空气阻力,则小球着地瞬间的重力势能是(选取O点所在平面为参考平面)( )
如图所示,小球的质量为m,自光滑的斜槽的顶端A无处速滑下,沿虚线轨迹落地,不计空气阻力,则小球着地瞬间的重力势能是(选取O点所在平面为参考平面)( )| A. | mgH | B. | -mgh | C. | 0 | D. | -mgH |
7.在物理学发展史上,许多科学家通过恰当地运用科学研究方法,超越了当时研究条件的局限性,取得了辉煌的研究成果,下列表述符合物理学史的是( )
| A. | 伽利略做的著名理想斜面实验其核心就是为了“冲淡”重力的影响 | |
| B. | 无论亚里士多德、伽利略还是笛卡尔都没有建立力的概念,而牛顿的高明之处在于他将物体间复杂多样的相互作用抽象为“力”,为提出牛顿第一定律而确立了一个重要的物理概念 | |
| C. | 英国物理学家麦克斯韦认为,磁场会在其周围空间激发一种电场,这种电场就是感生电场 | |
| D. | 机场、车站和重要活动场所的安检门可以探测人随身携带的金属物品,是利用静电感应的工作原理工作的 |
17.下列过程吸收能量的是( )
| A. | 重核裂变 | B. | 轻核聚变 | ||
| C. | 原子核的α衰变时 | D. | 原子从较低能级跃迁到较高能级 |
4.下列说法中正确的是( )
| A. | 发现天然放射现象的意义在于使人类认识到原子具有复杂的结构 | |
| B. | 结合能越大的原子核,原子核中的核子结合得越牢固,原子核越稳定 | |
| C. | 根据玻尔理论可知,氢原子核外电子跃迁过程中电子的电势能和动能之和不守恒 | |
| D. | 在光电效应实验中,用同种频率的光照射不同的金属表面,从金属表面逸出的光电子的最大初动能Ek越大,则这种金属的逸出功W0越小 | |
| E. | 已知${\;}_{90}^{234}$Th的半衰期是24天,48g的${\;}_{90}^{234}$Th经过72天后衰变了42g |
 水上滑梯可简化成如图所示的模型:倾角为θ=37°斜滑道AB和光滑圆弧滑道BC在B点相切连接,圆弧末端C点的切线水平,C点到水面的距离h=2m,顶点A距水面的高度H=12m,A、B的高度差HAB=9m,一质量m=50kg的人从滑道起点A点无初速地自由滑下,人与滑道AB间的动摩擦因数均为μ=0.25.(取重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6,人在运动过程中可视为质点)
水上滑梯可简化成如图所示的模型:倾角为θ=37°斜滑道AB和光滑圆弧滑道BC在B点相切连接,圆弧末端C点的切线水平,C点到水面的距离h=2m,顶点A距水面的高度H=12m,A、B的高度差HAB=9m,一质量m=50kg的人从滑道起点A点无初速地自由滑下,人与滑道AB间的动摩擦因数均为μ=0.25.(取重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6,人在运动过程中可视为质点)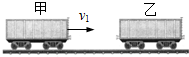 在列车编组站里,一辆m1=3.6×104kg的甲货车在平直轨道上以v1=2m/s的速度运动,碰上一辆m2=2.4×104kg的静止的乙货车,它们碰撞后结合在一起继续运动,求货车碰撞后运动的速度以及甲货车在碰撞过程中动量的变化量.
在列车编组站里,一辆m1=3.6×104kg的甲货车在平直轨道上以v1=2m/s的速度运动,碰上一辆m2=2.4×104kg的静止的乙货车,它们碰撞后结合在一起继续运动,求货车碰撞后运动的速度以及甲货车在碰撞过程中动量的变化量.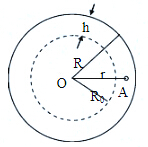 新发现行星,其星球半径为R=6400km,且由通常的水形成的海洋覆盖着它的所有表面,海洋的深度为h=10km,学者们对该行星进行探测时发现,当把试验用的样品浸入行星海洋的不同深度时,各处的自由落体加速度以相当高的精确度保持不变,已知万有引力常量G=6.67×10-11N•m2/kg2,海水密度ρ=1.0×103kg/m3,半径为R的球面面积公式S=4πR2.
新发现行星,其星球半径为R=6400km,且由通常的水形成的海洋覆盖着它的所有表面,海洋的深度为h=10km,学者们对该行星进行探测时发现,当把试验用的样品浸入行星海洋的不同深度时,各处的自由落体加速度以相当高的精确度保持不变,已知万有引力常量G=6.67×10-11N•m2/kg2,海水密度ρ=1.0×103kg/m3,半径为R的球面面积公式S=4πR2.