题目内容
4. 如图所示是汽车液压刹车装置的一部分.该装置中AOB实为一个杠杆,O是杠杆的支点,请画出刹车时动力F1的力臂L1和它所受的阻力F2.
如图所示是汽车液压刹车装置的一部分.该装置中AOB实为一个杠杆,O是杠杆的支点,请画出刹车时动力F1的力臂L1和它所受的阻力F2.
分析 要区分力臂与力矩这两个不同的概念,力臂是从支点到力的作用线的距离,即垂线段的长.还要搞清阻力是阻碍杠杆转动,是杠杆受到的外力.
解答 解:所画的动力臂及阻力如图所示:
因为动力臂就是从支点到动力作用线的距离,所以从支点向F1作用线画垂线段即可得到,如图所示的l1;而阻力是阻碍杠杆转动的力,只能是活塞阻碍B点的力,方向向右,如图所示的F2.
答:如图所示 l1、以及F2为所求.
点评 这是考察力臂概念的题,只要作图按要求就能完成.根据力臂的定义,是从支点到力的作用线的距离.
根据阻力的概念阻碍AOB转动的力为阻力,所以阻力为活塞对B点向左的力F2

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
18.在水平面上有一个小物块质量为m,由0点从静止开始沿水平面做匀加速直线运动,经过A、B、C三点,A、B、C三点到0点距离分别为x1、x2、x3,由0点到A、B、C所用时间分别为t1、t2、t3,下列结论正确的是( )
| A. | $\frac{x_1}{{{t_1}^2}}=\frac{x_2}{{{t_2}^2}}=\frac{x_3}{{{t_3}^2}}$ | B. | $\frac{x_1}{t_1}<\frac{x_2}{t_2}<\frac{x_3}{t_3}$ | ||
| C. | $\frac{x_1}{t_1}=\frac{x_2}{t_2}=\frac{x_3}{t_3}$ | D. | $\frac{x_1}{{{t_1}^2}}<\frac{x_2}{{{t_2}^2}}<\frac{x_3}{{{t_3}^2}}$ |
12. 如图所示,生产车间有两个相互垂直且等高的水平传送带甲和乙(速度恒定不变),甲的速度为v0.物体离开甲前与甲的速度相同,并平稳地传到乙上,乙的速度也为v0.物体与乙之间的动摩擦因数为μ.重力加速度为 g.若乙的宽度足够大,下列说法正确的( )
如图所示,生产车间有两个相互垂直且等高的水平传送带甲和乙(速度恒定不变),甲的速度为v0.物体离开甲前与甲的速度相同,并平稳地传到乙上,乙的速度也为v0.物体与乙之间的动摩擦因数为μ.重力加速度为 g.若乙的宽度足够大,下列说法正确的( )
 如图所示,生产车间有两个相互垂直且等高的水平传送带甲和乙(速度恒定不变),甲的速度为v0.物体离开甲前与甲的速度相同,并平稳地传到乙上,乙的速度也为v0.物体与乙之间的动摩擦因数为μ.重力加速度为 g.若乙的宽度足够大,下列说法正确的( )
如图所示,生产车间有两个相互垂直且等高的水平传送带甲和乙(速度恒定不变),甲的速度为v0.物体离开甲前与甲的速度相同,并平稳地传到乙上,乙的速度也为v0.物体与乙之间的动摩擦因数为μ.重力加速度为 g.若乙的宽度足够大,下列说法正确的( )| A. | 物体刚滑上乙传送带时,受到摩擦力大小为μmg | |
| B. | 物体刚滑上乙传送带时,受到摩擦力大小为$\sqrt{2}$μmg | |
| C. | 物体在乙上侧向( 垂直于乙的运动方向) 滑过的距离为$\frac{\sqrt{2}{{v}_{0}}^{2}}{2μg}$ | |
| D. | 物体在乙上侧向( 垂直于乙的运动方向) 滑过的距离为$\frac{\sqrt{2}{{v}_{0}}^{2}}{μg}$ |
9. 如图所示,两个固定的相同细环相距一定的距离,同轴放置,O1、O2分别为两环的圆心,两环分别带有均匀分布的等量异种电荷.一带正电的粒子从很远处沿轴线飞来并穿过两环.则在带电粒子运动过程中( )
如图所示,两个固定的相同细环相距一定的距离,同轴放置,O1、O2分别为两环的圆心,两环分别带有均匀分布的等量异种电荷.一带正电的粒子从很远处沿轴线飞来并穿过两环.则在带电粒子运动过程中( )
 如图所示,两个固定的相同细环相距一定的距离,同轴放置,O1、O2分别为两环的圆心,两环分别带有均匀分布的等量异种电荷.一带正电的粒子从很远处沿轴线飞来并穿过两环.则在带电粒子运动过程中( )
如图所示,两个固定的相同细环相距一定的距离,同轴放置,O1、O2分别为两环的圆心,两环分别带有均匀分布的等量异种电荷.一带正电的粒子从很远处沿轴线飞来并穿过两环.则在带电粒子运动过程中( )| A. | 在O1点粒子加速度方向向右 | |
| B. | 从O1到O2过程粒子电势能一直增加 | |
| C. | 轴线上O1点右侧存在一点,粒子在该点动能最小 | |
| D. | 轴线上O1点右侧,O2点左侧都存在场强为零的点,它们关于O1、O2连线中点对称 |
16. 如图,a、b两个带电小球,质量分别为ma,mb,用绝缘细线悬挂,细线无弹性且不会被拉断.两球静止时,它们距水平地面的高度均为h(h尽够大),绳与竖直方向的夹角分别为α和β(α<β).若剪断细线Oc,空气阻力不计,两球电量不变,重力加速度为g.则下列说法正确的是( )
如图,a、b两个带电小球,质量分别为ma,mb,用绝缘细线悬挂,细线无弹性且不会被拉断.两球静止时,它们距水平地面的高度均为h(h尽够大),绳与竖直方向的夹角分别为α和β(α<β).若剪断细线Oc,空气阻力不计,两球电量不变,重力加速度为g.则下列说法正确的是( )
 如图,a、b两个带电小球,质量分别为ma,mb,用绝缘细线悬挂,细线无弹性且不会被拉断.两球静止时,它们距水平地面的高度均为h(h尽够大),绳与竖直方向的夹角分别为α和β(α<β).若剪断细线Oc,空气阻力不计,两球电量不变,重力加速度为g.则下列说法正确的是( )
如图,a、b两个带电小球,质量分别为ma,mb,用绝缘细线悬挂,细线无弹性且不会被拉断.两球静止时,它们距水平地面的高度均为h(h尽够大),绳与竖直方向的夹角分别为α和β(α<β).若剪断细线Oc,空气阻力不计,两球电量不变,重力加速度为g.则下列说法正确的是( )| A. | a球先落地,b球后落地 | |
| B. | 落地时,a、b两球的动能和为(ma+mb)gh | |
| C. | 整个运动过程中,a、b系统的机械能守恒 | |
| D. | 落地时,a、b水平速度不为零并且有大小相等,且方向相反 |
13.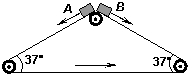 如图所示,三角形传送带以1m/s的速度逆时针匀速运动,两边的传送带长都是2m,且与水平方向的夹角均为37°.现有两小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑,物块与传送带间的动摩擦因数都是0.5,(g取10m/s2,sin37°=0.6,cos37°=0.8)下列说法不正确的是( )
如图所示,三角形传送带以1m/s的速度逆时针匀速运动,两边的传送带长都是2m,且与水平方向的夹角均为37°.现有两小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑,物块与传送带间的动摩擦因数都是0.5,(g取10m/s2,sin37°=0.6,cos37°=0.8)下列说法不正确的是( )
 如图所示,三角形传送带以1m/s的速度逆时针匀速运动,两边的传送带长都是2m,且与水平方向的夹角均为37°.现有两小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑,物块与传送带间的动摩擦因数都是0.5,(g取10m/s2,sin37°=0.6,cos37°=0.8)下列说法不正确的是( )
如图所示,三角形传送带以1m/s的速度逆时针匀速运动,两边的传送带长都是2m,且与水平方向的夹角均为37°.现有两小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑,物块与传送带间的动摩擦因数都是0.5,(g取10m/s2,sin37°=0.6,cos37°=0.8)下列说法不正确的是( )| A. | 物块A先到达传送带底端 | |
| B. | 物块A、B同时到达传送带底端 | |
| C. | 传送带对物块A、B均做负功 | |
| D. | 物块A、B传送带上的划痕长度之比为1:3 |