题目内容
11. 如图所示为一条平直公路,其中A点左边的路段为足够长的柏油路面,A点右边路段为水泥路面,已知汽车轮胎与柏油路面的动摩擦因数为μ1,与水泥路面的动摩擦因数为μ2.某次测试发现,当汽车以速度v0在路面行驶时,刚过A点时紧急刹车后(车轮立即停止转动),汽车要滑行到B点才能停下.现在,该汽车以2v0的速度在柏油路面上向右行驶,突然发现B处有障碍物,需在A点左侧的柏油路段上某处紧急刹车,才能避免撞上障碍物.(重力加速度为g)
如图所示为一条平直公路,其中A点左边的路段为足够长的柏油路面,A点右边路段为水泥路面,已知汽车轮胎与柏油路面的动摩擦因数为μ1,与水泥路面的动摩擦因数为μ2.某次测试发现,当汽车以速度v0在路面行驶时,刚过A点时紧急刹车后(车轮立即停止转动),汽车要滑行到B点才能停下.现在,该汽车以2v0的速度在柏油路面上向右行驶,突然发现B处有障碍物,需在A点左侧的柏油路段上某处紧急刹车,才能避免撞上障碍物.(重力加速度为g)(1)求水泥路面AB段的长度;
(2)为防止汽车撞上障碍物,开始紧急刹车的位置距A点的距离至少为多少?若刚好不撞上,汽车紧急刹车的时间是多少?
分析 (1)汽车在水泥路上刹车做匀减速直线运动,根据牛顿第二定律求出汽车在水泥路面上的加速度,根据位移速度公式求出水泥路面AB段的长度;
(2)根据题意,汽车如果不撞上障碍物B,则在A点的速度应为v0,根据牛顿第二定律求出在柏油路面上的加速度,根据速度时间公式求出在柏油路上运动的时间及在水泥路面上运动的时间,两段时间之和即为总时间.根据速度位移公式求出开始紧急刹车的位置距A点的距离.
解答 解:(1)水泥路面上运动的加速度大小为a2,则:
μ2mg=ma2
由:$-2{a}_{2}{x}_{2}=0-{{v}_{0}}^{2}$
解得:${x}_{2}=\frac{{{v}_{0}}^{2}}{2{μ}_{2}g}$
(2)根据题意,汽车如果刚好不撞上障碍物B,在A点的速度应为v0,在柏油路上运动时间为t1,加速度大小为a1,运动位移为x1,则:
μ1mg=ma1
v0-2v0=-a1t1
$-2{a}_{1}{x}_{1}={{v}_{0}}^{2}-4{{v}_{0}}^{2}$
解得:${t}_{1}=\frac{{v}_{0}}{{μ}_{1}g}$,${x}_{1}=\frac{3{{v}_{0}}^{2}}{2{μ}_{1}g}$
在水泥路面上运动时间为t2则:0-v0=-a2t2
解得:${t}_{2}=\frac{{v}_{0}}{{μ}_{2}g}$
汽车不撞上,则应在A点左侧距A点距离大于${x}_{1}=\frac{3{{v}_{0}}^{2}}{2{μ}_{1}g}$的位置开始紧急刹车.
汽车运动的时间:t=${t}_{1}+{t}_{2}=\frac{{v}_{0}}{{μ}_{1}g}+\frac{{v}_{0}}{{μ}_{2}g}=\frac{({μ}_{1}+{μ}_{2}){v}_{0}}{{μ}_{1}{μ}_{2}g}$
答:(1)求水泥路面AB段的长度为$\frac{{{v}_{0}}^{2}}{2{μ}_{2}g}$;
(2)为防止汽车撞上障碍物,开始紧急刹车的位置距A点的距离至少为$\frac{3{{v}_{0}}^{2}}{2{μ}_{1}g}$;
若刚好不撞上,汽车紧急刹车的时间是$\frac{({μ}_{1}+{μ}_{2}){v}_{0}}{{μ}_{1}{μ}_{2}g}$.
点评 本题主要考查了牛顿第二定律及运动学基本公式的直接应用,知道汽车如果不撞上障碍物B,则在A点的速度应为v0,难度适中.

| A. | 一定是电源连接到金属外壳上了 | |
| B. | 一定是与电源相连的机芯与金属外壳间绝缘不良,导致漏电所致 | |
| C. | 可能是该设备的金属外壳没有接地 | |
| D. | 可能是电源中的交变电流“通过”了由机芯和金属外壳构成的“电容器” |
 如图所示,理想变压器原线圈通过理想电流表接在输出电压u=220$\sqrt{2}$sin100πtV的交流电源的两端,副线圈中接有理想电压表及阻值R=50Ω的负载电阻,已知原、副线圈匝数之比为11:1,则下列说法中正确的是( )
如图所示,理想变压器原线圈通过理想电流表接在输出电压u=220$\sqrt{2}$sin100πtV的交流电源的两端,副线圈中接有理想电压表及阻值R=50Ω的负载电阻,已知原、副线圈匝数之比为11:1,则下列说法中正确的是( )| A. | 电流表的示数为4.4A | |
| B. | 原线圈的输入功率为16W | |
| C. | 电压表的示数为20V | |
| D. | 通过电阻R的交变电流的频率为100Hz |
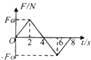 一质点在某一外力F作用下由静止开始运动,力F的大小随时间t变化的图象如图所示,其方向始终在一条直线上,在0-8s内,下列说法正确的是( )
一质点在某一外力F作用下由静止开始运动,力F的大小随时间t变化的图象如图所示,其方向始终在一条直线上,在0-8s内,下列说法正确的是( )| A. | 在0-2s内质点做匀加速运动,第2s末其速度达到最大值 | |
| B. | 第4s末质点的加速度为零,速度也刚好为零 | |
| C. | 质点做变加速直线运动,第6s末加速度最大,且离出发位置最远 | |
| D. | 在0-8s内,质点一直向同一个方向做直线运动,在第8s末速度和加速度都为零,且离出发点最远 |
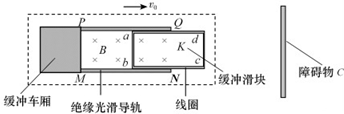
| A. | 线圈中的感应电流沿逆时针方向(俯视),最大感应电流为$\frac{BL{v}_{0}}{R}$ | |
| B. | 线圈对电磁铁的作用力使缓冲车厢减速运动,从而实现缓冲 | |
| C. | 此过程中,线圈abcd产生的焦耳热为Q=$\frac{1}{2}$mv02 | |
| D. | 此过程中,通过线圈abcd的电荷量为q=$\frac{B{L}^{2}}{R}$ |

| A. | 这列波的波长是4m | |
| B. | 这列波的传播速度是1.25m/s | |
| C. | M点以后的各质点开始振动时的方向都沿y轴正方向 | |
| D. | 质点Q经过7s时,第一次到达波峰 |
 2014年11月12日,“菲莱”着陆器成功在67P彗星上实现着陆,这是人类首次实现在彗星上软着陆,被称为人类历史上最伟大冒险之旅.载有“菲莱”的“罗赛塔”飞行器历经十年的追逐,被67P彗星俘获后经过一系列变轨,成功的将“菲莱”着陆器弹出,准确得在彗星表面着陆.如图所示,轨道1和轨道2是“罗赛塔”绕彗星环绕的两个圆轨道,B点是轨道2上的一个点,若在轨道1上找一点A,使A与B的连线与BO连线的最大夹角为θ,则“罗赛塔”在轨道1、2上运动的周期之比$\frac{{T}_{1}}{{T}_{2}}$为( )
2014年11月12日,“菲莱”着陆器成功在67P彗星上实现着陆,这是人类首次实现在彗星上软着陆,被称为人类历史上最伟大冒险之旅.载有“菲莱”的“罗赛塔”飞行器历经十年的追逐,被67P彗星俘获后经过一系列变轨,成功的将“菲莱”着陆器弹出,准确得在彗星表面着陆.如图所示,轨道1和轨道2是“罗赛塔”绕彗星环绕的两个圆轨道,B点是轨道2上的一个点,若在轨道1上找一点A,使A与B的连线与BO连线的最大夹角为θ,则“罗赛塔”在轨道1、2上运动的周期之比$\frac{{T}_{1}}{{T}_{2}}$为( )| A. | sin3θ | B. | $\frac{1}{si{n}^{3}θ}$ | C. | $\sqrt{si{n}^{3}θ}$ | D. | $\sqrt{\frac{1}{si{n}^{3}θ}}$ |

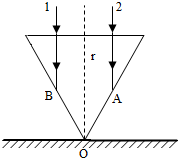 在桌面上有一个倒立的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示,有一半径为r的圆柱形平行光束垂直入射到圆锥的底面上,光束的中心轴与圆锥的轴重合,已知玻璃的折射率为n=$\sqrt{3}$,则:
在桌面上有一个倒立的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示,有一半径为r的圆柱形平行光束垂直入射到圆锥的底面上,光束的中心轴与圆锥的轴重合,已知玻璃的折射率为n=$\sqrt{3}$,则: