题目内容
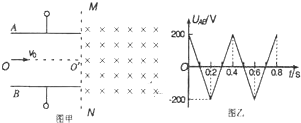
1.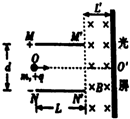 如图所示,一对平行金属板MM′、NN′水平放置.板长L=0.4m.板间距离d=0.4m.将两板接在-个电压可以调节的电源上(圈中未画出).MM′接电源的正极.在两板的右侧存在水平方向的匀强磁场.磁场的方向垂直于纸面向里.磁感应强度的大小B=0 25T.NN′在磁场的左侧边界上,磁场的右侧边界竖直放置-个足够长的光屏,磁场的宽度L′=0.2m,现有比荷为为$\frac{q}{m}$=2×105c/kg的带正电的粒子束.沿两扳的中轴线00′以相同的速度不停地射入,当两板之间的电压为0V时,粒子刚好不能打在光屏上.不计粒子重力.
如图所示,一对平行金属板MM′、NN′水平放置.板长L=0.4m.板间距离d=0.4m.将两板接在-个电压可以调节的电源上(圈中未画出).MM′接电源的正极.在两板的右侧存在水平方向的匀强磁场.磁场的方向垂直于纸面向里.磁感应强度的大小B=0 25T.NN′在磁场的左侧边界上,磁场的右侧边界竖直放置-个足够长的光屏,磁场的宽度L′=0.2m,现有比荷为为$\frac{q}{m}$=2×105c/kg的带正电的粒子束.沿两扳的中轴线00′以相同的速度不停地射入,当两板之间的电压为0V时,粒子刚好不能打在光屏上.不计粒子重力.(1)带电粒子的初速度为多大?
(2)要使粒子能从两板MM′、NN′之间射出,加在两板之同的电压范围为多大?
(3)如果从零开始连续调节两板所接电源(内阻不计)的电压,粒子打在光屏上的位置将会发生变化,那么,粒子束打在光屏上的区域的长度是多少?(保留根号)
分析 (1)带电粒子在磁场中发生偏转,当运动的轨迹刚好与屏相切时,粒子刚好不能打在光屏上,由洛伦兹力提供向心力即可解答;
(2)带电粒子在电场中发生偏转,由平抛运动的规律,即可求解;
(3)根据带电粒子在磁场中运动的规律和从电场中射出时速度的方向,判断出能打到光屏的位置.
解答 解:(1)当两板之间的电压为0V时,粒子沿直线方向穿过电场的区域,带电粒子在磁场中发生偏转,由洛伦兹力提供向心力,得:
$q{v}_{0}B=\frac{m{v}_{0}^{2}}{r}$
当运动的轨迹刚好与屏相切时,粒子刚好不能打在光屏上,则:r=L′
所以,粒子的初速度:${v}_{0}=\frac{qBL′}{m}$
代入数据得:${v}_{0}=1{0}^{4}$m/s
(2)由图可知电场的方向向下,正电荷在电场中受到的电场力的方向向下,当粒子恰好从N′点射出时,偏转量:$y=\frac{1}{2}d=\frac{1}{2}×0.4m=0.2$m
水平方向:L=v0t
粒子受到的电场力:$F=qE=\frac{q{U}_{m}}{d}$
粒子的加速度:$a=\frac{F}{m}$
偏转量:$y=\frac{1}{2}a{t}^{2}$
联立方程,整理得:${U}_{m}=\frac{2ym{v}_{0}^{2}d}{q{L}^{2}}=500$V
加在两板之同的电压范围为U≤500V
(3)正电荷在磁场中受到的安培力的方向向左,当偏转电等于0时,粒子打在光屏上的位置在最上面,当偏转电压是500V时,粒子的位置在最下面,如图:
粒子沿竖直方向的分速度:${v}_{y}=at=\frac{q{U}_{m}}{md}•\frac{L}{{v}_{0}}=1{0}^{4}$m/s
粒子在电场中的偏转角:$tanθ=\frac{{v}_{y}}{{v}_{0}}=1$
所以偏转角:θ=45°
粒子的合速度:$v=\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}=\sqrt{2}×1{0}^{4}$m/s
此时,粒子在磁场中的偏转半径:$r′=\frac{mv}{qB}=\frac{\sqrt{2}m{v}_{0}}{qB}=\sqrt{2}L′$=$\sqrt{2}$0.2m,由几何关系可得,此时粒子做匀速圆周运动的圆心在O′点,如图,则打在光屏上的位置到O′点的距离是r′,粒子束打在光屏上的区域的长度(绿色线)是:x=r+r′=0.2m+0.2$\sqrt{2}$m≈0.48m
答:(1)带电粒子的初速度为${v}_{0}=1{0}^{4}$m/s.
(2)要使粒子能从两板MM′、NN′之间射出,加在两板之同的电压范围为U≤500V
(3)如果从零开始连续调节两板所接电源(内阻不计)的电压,粒子打在光屏上的位置将会发生变化,那么,粒子束打在光屏上的区域的长度是0.48m
点评 本题考查了粒子在电场与磁场中的运动,分析清楚粒子运动过程,正确画出粒子运动的轨迹是正确解题的前提与关键.

 安徽首家滑雪场正式落户国家AAAA级旅游景区-安庆巨石山.2014年元旦已正式“开滑”.如图所示,滑雪者从O点由静止沿斜面自由下滑,接着在水平面上滑至N点停下.斜面、水平面与滑雪板之间的动摩擦因数都为μ=0.1.滑雪者(包括滑雪板)的质量为m=50kg,g取10m/s2,O、N两点间的水平距离为s=100m.在滑雪者经过ON段运动的过程中,克服摩擦力做的功( )
安徽首家滑雪场正式落户国家AAAA级旅游景区-安庆巨石山.2014年元旦已正式“开滑”.如图所示,滑雪者从O点由静止沿斜面自由下滑,接着在水平面上滑至N点停下.斜面、水平面与滑雪板之间的动摩擦因数都为μ=0.1.滑雪者(包括滑雪板)的质量为m=50kg,g取10m/s2,O、N两点间的水平距离为s=100m.在滑雪者经过ON段运动的过程中,克服摩擦力做的功( )| A. | 1250J | B. | 2500J | C. | 5000J | D. | 7500J |
 如图所示的两种电路中,电源相同,各电阻阻值相等,各电流表的内阻相等且不可忽略不计.电流表A1、A2、A3、A4读出的电流值分别为I1、I2、I3、I4,下列关系式中正确的是( )
如图所示的两种电路中,电源相同,各电阻阻值相等,各电流表的内阻相等且不可忽略不计.电流表A1、A2、A3、A4读出的电流值分别为I1、I2、I3、I4,下列关系式中正确的是( )| A. | I1=I2 | B. | I1<I4 | C. | I2=2I1 | D. | I2<I3+I4 |
| A. | 1.2×104N | B. | 2.4×103N | C. | 2.0×103N | D. | 5.9×102N |
 如图所示,劲度系数为k的轻弹簧一端固定在墙上,另一端与置于水平面上的质量为m的小物体接触(未连接),如图中O点,弹簧水平且无形变.用水平力F缓慢向左推动物体,在弹性限度内弹簧长度被压缩了x0,如图中B点,此时物体静止.撤去F后,物体开始向右运动,运动的最大距离距B点为3x0,C点是物体向右运动过程中弹力和摩擦力大小相等的位置,物体与水平面间的动摩擦因数为μ,重力加速度为g.则( )
如图所示,劲度系数为k的轻弹簧一端固定在墙上,另一端与置于水平面上的质量为m的小物体接触(未连接),如图中O点,弹簧水平且无形变.用水平力F缓慢向左推动物体,在弹性限度内弹簧长度被压缩了x0,如图中B点,此时物体静止.撤去F后,物体开始向右运动,运动的最大距离距B点为3x0,C点是物体向右运动过程中弹力和摩擦力大小相等的位置,物体与水平面间的动摩擦因数为μ,重力加速度为g.则( )| A. | 撤去F时,物体的加速度最大,大小为$\frac{k{x}_{0}}{m}$-μg | |
| B. | 物体先做加速度逐渐变小的加速运动,再做加速度逐渐变大的减速运动,最后做匀减速运动 | |
| C. | 从B→C位置物体弹簧弹性势能的减少量大于物体动能的增加量 | |
| D. | 撤去F后,物体向右运动到O点时的动能最大 |
| A. | 卫星离地球越远,运行周期越小 | |
| B. | 卫星运行的瞬时速度可以大于7.9km/s | |
| C. | 同一圆轨道上运行的两颗卫星,线速度大小可能不同 | |
| D. | 地球同步卫星可以经过地球两极上空 |
 某电视台闯关竞技节目的第一关是雪滑梯,其结构可以简化为下图模型,雪滑梯顶点距地面高h=15m,滑梯斜面部分长l=25m,在水平部分距离斜道底端为x0=20m处有一海绵坑.比赛时参赛运动员乘坐一质量为M的雪轮胎从赛道顶端滑下,在水平雪道上某处翻离雪轮胎滑向海棉坑,运动员停在距离海绵坑1m范围内算过关.已知雪轮胎与雪道间的动摩擦因数μ1=0.3,运动员与雪道间动摩擦因数为μ2=0.8,假没运动员离开雪轮胎的时间不计,运动员落到雪道上时的水平速度不变,求质量为m的运动员(可视为质点)在水平雪道上的什么区域离开雪轮胎才能闻关成功.
某电视台闯关竞技节目的第一关是雪滑梯,其结构可以简化为下图模型,雪滑梯顶点距地面高h=15m,滑梯斜面部分长l=25m,在水平部分距离斜道底端为x0=20m处有一海绵坑.比赛时参赛运动员乘坐一质量为M的雪轮胎从赛道顶端滑下,在水平雪道上某处翻离雪轮胎滑向海棉坑,运动员停在距离海绵坑1m范围内算过关.已知雪轮胎与雪道间的动摩擦因数μ1=0.3,运动员与雪道间动摩擦因数为μ2=0.8,假没运动员离开雪轮胎的时间不计,运动员落到雪道上时的水平速度不变,求质量为m的运动员(可视为质点)在水平雪道上的什么区域离开雪轮胎才能闻关成功.