题目内容
13. 如图所示,劲度系数为k的轻弹簧一端固定在墙上,另一端与置于水平面上的质量为m的小物体接触(未连接),如图中O点,弹簧水平且无形变.用水平力F缓慢向左推动物体,在弹性限度内弹簧长度被压缩了x0,如图中B点,此时物体静止.撤去F后,物体开始向右运动,运动的最大距离距B点为3x0,C点是物体向右运动过程中弹力和摩擦力大小相等的位置,物体与水平面间的动摩擦因数为μ,重力加速度为g.则( )
如图所示,劲度系数为k的轻弹簧一端固定在墙上,另一端与置于水平面上的质量为m的小物体接触(未连接),如图中O点,弹簧水平且无形变.用水平力F缓慢向左推动物体,在弹性限度内弹簧长度被压缩了x0,如图中B点,此时物体静止.撤去F后,物体开始向右运动,运动的最大距离距B点为3x0,C点是物体向右运动过程中弹力和摩擦力大小相等的位置,物体与水平面间的动摩擦因数为μ,重力加速度为g.则( )| A. | 撤去F时,物体的加速度最大,大小为$\frac{k{x}_{0}}{m}$-μg | |
| B. | 物体先做加速度逐渐变小的加速运动,再做加速度逐渐变大的减速运动,最后做匀减速运动 | |
| C. | 从B→C位置物体弹簧弹性势能的减少量大于物体动能的增加量 | |
| D. | 撤去F后,物体向右运动到O点时的动能最大 |
分析 本题通过分析物体的受力情况,来确定其运动情况:撤去F后,物体水平方向上受到弹簧的弹力和滑动摩擦力,滑动摩擦力大小不变,而弹簧的弹力随着压缩量的减小而减小,物体先做变加速运动,再做变减速运动,最后物体离开弹簧后做匀减速运动;撤去F后,根据牛顿第二定律求解物体刚运动时的加速度大小;物体离开弹簧后通过的最大距离为2x0,由动能定理求解弹力滑动摩擦力力所做的总功;当弹簧的弹力与电场力、滑动摩擦力的合力大小相等、方向相反时,速度最大,可求得此时弹簧的压缩量,即可求解物体开始向左运动到速度最大的过程中克服摩擦力做的功.
解答 解:A、撤去F后一直到物体停止运动的过程,对物体应用动能定理可得,$\frac{1}{2}$k${x}_{0}^{2}$-3μmgx0=0,故有kx0=6μmg故物体的加速度最大位置就是初始位置,大小为$\frac{k{x}_{0}}{m}$-μg,故A正确;
B、撤去F后,物体水平方向上受到弹簧的弹力和滑动摩擦力,滑动摩擦力不变,而弹簧的弹力随着压缩量的减小而减小,弹簧的弹力随着压缩量的减小而减小,加速度先减小后增大,物体先做变加速运动,再做变减速运动,物体离开弹簧后做匀减速运动.故B正确;
C、由动能定理可知,弹力做功减去摩擦力做的功的绝对值等于物体动能的增加量,故弹簧弹性势能的减少量大于物体动能的增加量,故C正确;
D、物体向右运动过程中,加速度为零时,速度最大,故到C点时的动能最大,故D错误.
故选:ABC.
点评 本题分析物体的受力情况和运动情况是解答的关键,要抓住加速度与合外力成正比,即可得到加速度是变化的.对于物体弹簧弹性势能的减少量与物体动能的增加量间的关系通常应用动能定理结合功能关系解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8. 半圆柱体P放在粗糙的水平地面上,其右端有固定放置的竖直挡板MN.在P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于静止状态.如图所示是这个装置的纵截面图.若用外力使MN保持竖直地缓慢向右移动,在Q落到地面以前,发现P始终保持静止.在此过程中,下列说法中正确的是( )
半圆柱体P放在粗糙的水平地面上,其右端有固定放置的竖直挡板MN.在P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于静止状态.如图所示是这个装置的纵截面图.若用外力使MN保持竖直地缓慢向右移动,在Q落到地面以前,发现P始终保持静止.在此过程中,下列说法中正确的是( )
 半圆柱体P放在粗糙的水平地面上,其右端有固定放置的竖直挡板MN.在P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于静止状态.如图所示是这个装置的纵截面图.若用外力使MN保持竖直地缓慢向右移动,在Q落到地面以前,发现P始终保持静止.在此过程中,下列说法中正确的是( )
半圆柱体P放在粗糙的水平地面上,其右端有固定放置的竖直挡板MN.在P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于静止状态.如图所示是这个装置的纵截面图.若用外力使MN保持竖直地缓慢向右移动,在Q落到地面以前,发现P始终保持静止.在此过程中,下列说法中正确的是( )| A. | Q受到MN的弹力逐渐减小 | |
| B. | Q受到P的弹力逐渐减小 | |
| C. | Q受到MN和P的弹力之和保持不变 | |
| D. | P受到地面的支持力和摩擦力均保持不变 |
2. 在高能粒子研究中,往往要把一束含有大量质子和α粒子的混合粒子分离开,如图初速度可忽略的质子和α粒子,经电压为U的电场加速后,进入分离区.如果在分离区使用匀强电场或匀强磁场把粒子进行分离,所加磁场方向垂直纸面向里,所加电场方向竖直向下,则下列可行的方法是( )
在高能粒子研究中,往往要把一束含有大量质子和α粒子的混合粒子分离开,如图初速度可忽略的质子和α粒子,经电压为U的电场加速后,进入分离区.如果在分离区使用匀强电场或匀强磁场把粒子进行分离,所加磁场方向垂直纸面向里,所加电场方向竖直向下,则下列可行的方法是( )
 在高能粒子研究中,往往要把一束含有大量质子和α粒子的混合粒子分离开,如图初速度可忽略的质子和α粒子,经电压为U的电场加速后,进入分离区.如果在分离区使用匀强电场或匀强磁场把粒子进行分离,所加磁场方向垂直纸面向里,所加电场方向竖直向下,则下列可行的方法是( )
在高能粒子研究中,往往要把一束含有大量质子和α粒子的混合粒子分离开,如图初速度可忽略的质子和α粒子,经电压为U的电场加速后,进入分离区.如果在分离区使用匀强电场或匀强磁场把粒子进行分离,所加磁场方向垂直纸面向里,所加电场方向竖直向下,则下列可行的方法是( )| A. | 只能用电场 | B. | 只能用磁场 | ||
| C. | 电场和磁场都可以 | D. | 电场和磁场都不可以 |
3. 如图所示是骨折病人的牵引装置示意图,绳的一端固定,绕过定滑轮和动滑轮后挂着一个重物,与动滑轮相连的帆布带拉着病人的脚,整个装置在同一竖直平面内.下列采取的方法中,一定能使脚所受的拉力增大的是( )
如图所示是骨折病人的牵引装置示意图,绳的一端固定,绕过定滑轮和动滑轮后挂着一个重物,与动滑轮相连的帆布带拉着病人的脚,整个装置在同一竖直平面内.下列采取的方法中,一定能使脚所受的拉力增大的是( )
 如图所示是骨折病人的牵引装置示意图,绳的一端固定,绕过定滑轮和动滑轮后挂着一个重物,与动滑轮相连的帆布带拉着病人的脚,整个装置在同一竖直平面内.下列采取的方法中,一定能使脚所受的拉力增大的是( )
如图所示是骨折病人的牵引装置示意图,绳的一端固定,绕过定滑轮和动滑轮后挂着一个重物,与动滑轮相连的帆布带拉着病人的脚,整个装置在同一竖直平面内.下列采取的方法中,一定能使脚所受的拉力增大的是( )| A. | 只增大两个定滑轮间的距离(绳适当加长) | |
| B. | 保持两个定滑轮与动滑轮连线的张角不变,增加重物的质量 | |
| C. | 保持两个定滑轮与动滑轮连线的张角不变,将病人的脚向左移动(绳适当加长) | |
| D. | 增大两个定滑轮间的距离同时将病人的脚向左移动(绳适当加长) |

 2011年7月,杭州吴某徒手接住从10楼掉下的两岁小孩,被誉为“最美妈妈”.设小孩的质量m=10kg,从离地h1=28.5m高的阳台掉下,假设小孩在下落的整个过程中空气阻力为其重力的0.2倍.在小孩掉下后距地面高度为h2=1.5m处,吴某张开双臂接住小孩,接住后缓冲到地面时速度恰好为零,取g=10m/s2.求;(计算结果可以保留根号)
2011年7月,杭州吴某徒手接住从10楼掉下的两岁小孩,被誉为“最美妈妈”.设小孩的质量m=10kg,从离地h1=28.5m高的阳台掉下,假设小孩在下落的整个过程中空气阻力为其重力的0.2倍.在小孩掉下后距地面高度为h2=1.5m处,吴某张开双臂接住小孩,接住后缓冲到地面时速度恰好为零,取g=10m/s2.求;(计算结果可以保留根号)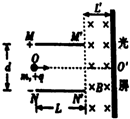 如图所示,一对平行金属板MM′、NN′水平放置.板长L=0.4m.板间距离d=0.4m.将两板接在-个电压可以调节的电源上(圈中未画出).MM′接电源的正极.在两板的右侧存在水平方向的匀强磁场.磁场的方向垂直于纸面向里.磁感应强度的大小B=0 25T.NN′在磁场的左侧边界上,磁场的右侧边界竖直放置-个足够长的光屏,磁场的宽度L′=0.2m,现有比荷为为$\frac{q}{m}$=2×105c/kg的带正电的粒子束.沿两扳的中轴线00′以相同的速度不停地射入,当两板之间的电压为0V时,粒子刚好不能打在光屏上.不计粒子重力.
如图所示,一对平行金属板MM′、NN′水平放置.板长L=0.4m.板间距离d=0.4m.将两板接在-个电压可以调节的电源上(圈中未画出).MM′接电源的正极.在两板的右侧存在水平方向的匀强磁场.磁场的方向垂直于纸面向里.磁感应强度的大小B=0 25T.NN′在磁场的左侧边界上,磁场的右侧边界竖直放置-个足够长的光屏,磁场的宽度L′=0.2m,现有比荷为为$\frac{q}{m}$=2×105c/kg的带正电的粒子束.沿两扳的中轴线00′以相同的速度不停地射入,当两板之间的电压为0V时,粒子刚好不能打在光屏上.不计粒子重力.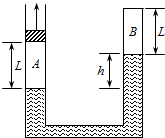 如图所示,内径粗细均匀的U形管,右侧B管上端封闭,左侧A管上端开口,管内注入水银,并在A管内装配有光滑的、质量可以不计的活塞,使两管中均封入L=25cm的空气柱,活塞上方的大气压强为P0=76cmHg,这时两管内水银面高度差h=6cm.今用外力竖直向上缓慢地拉活塞,直至使两管中水银面相平.设温度保持不变,则:A管中活塞向上移动距离是多少?
如图所示,内径粗细均匀的U形管,右侧B管上端封闭,左侧A管上端开口,管内注入水银,并在A管内装配有光滑的、质量可以不计的活塞,使两管中均封入L=25cm的空气柱,活塞上方的大气压强为P0=76cmHg,这时两管内水银面高度差h=6cm.今用外力竖直向上缓慢地拉活塞,直至使两管中水银面相平.设温度保持不变,则:A管中活塞向上移动距离是多少?