题目内容
10.两颗人造卫星绕地球做稳定的匀速圆周运动,它们的动能相等,它们的质量之比为1:4,则它们的( )| A. | 半径之比为1:2 | B. | 速率之比为4:1 | C. | 周期之比为1:4 | D. | 向心力之比为4:1 |
分析 卫星绕地球做匀速圆周运动时,由地球的万有引力提供向心力,根据万有引力定律和向心力公式得到卫星的线速度、周期、向心加速度、向心力与轨道半径的关系式,再求解比值.
解答 解:A、两颗人造卫星绕地球做稳定的匀速圆周运动,它们的动能相等,它们的质量之比为1:4,
根据EK=$\frac{1}{2}$mv2,
所以速率之比为2:1,
卫星做圆周运动,由万有引力提供向心力,则有:F=$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r=m$\frac{{v}^{2}}{r}$
v=$\sqrt{\frac{GM}{r}}$,
所以半径之比为1:4,故AB错误;
C、T=2π $\sqrt{\frac{{r}^{3}}{GM}}$,所以周期之比为1:8,故C错误;
D、F=$\frac{GMm}{{r}^{2}}$,所以向心力之比为4:1,故D正确;
故选:D.
点评 解答本题关键要掌握万有引力充当卫星的向心力这一基本思路,再灵活选择向心力公式的形式,即可轻松解答.

练习册系列答案
相关题目
18.理想实验是科学研究中的一种重要方法,它把可靠事实与逻辑思维结合起来,可以深刻地揭示自然规律,以下实验中属于理想实验的是( )
| A. | 验证平行四边形定则 | B. | 伽利略的斜面实验 | ||
| C. | 用弹簧验证胡克定律源 | D. | 利用自由落体运动测定反应时间 |
15.下列有关物理史实的叙述中正确的是目( )
| A. | 电荷周围存在由它产生的电场的观点,最早由奥斯特提出的 | |
| B. | 密立根通过“油滴实验”最早测定了元电荷e的电荷量 | |
| C. | 能测量带电粒子的质量和分析同位素的质谱仪,最初是由洛伦兹设计的 | |
| D. | 法拉第电磁感应定律最先是由法拉第提出的 |
19.天文学家发现某恒星有一颗行星在圆形轨道上绕其运动,并测出了行星的轨道半径R和公转周期T,已知引力常量为G,由此可算出( )
| A. | 恒星质量 | B. | 恒星平均密度 | C. | 行星质量 | D. | 行星半径 |
 如图所示,位于竖直面内的曲线轨道的最低点B的切线沿水平方向,且与一位于同一竖直面内、半径R=0.40m的光滑圆形轨道平滑连接.现有一质量m=0.15kg的滑块(可视为质点),从位于轨道上的A点由静止开始滑下,滑块经B点后恰好能通过圆形轨道的最高点C.已知A点到B点的高度h=1.5m,重力加速度g=10m/s2,空气阻力可忽略不计.
如图所示,位于竖直面内的曲线轨道的最低点B的切线沿水平方向,且与一位于同一竖直面内、半径R=0.40m的光滑圆形轨道平滑连接.现有一质量m=0.15kg的滑块(可视为质点),从位于轨道上的A点由静止开始滑下,滑块经B点后恰好能通过圆形轨道的最高点C.已知A点到B点的高度h=1.5m,重力加速度g=10m/s2,空气阻力可忽略不计. 平直路上向右运动的小车内,用细绳a和细绳b系住一个质量为3kg的小球,细绳a与竖直方向夹角θ=37°,细绳b水平(如图所示),取g=10m/s2.求:(已知:sin 37°=0.6,cos 37°=0.8)
平直路上向右运动的小车内,用细绳a和细绳b系住一个质量为3kg的小球,细绳a与竖直方向夹角θ=37°,细绳b水平(如图所示),取g=10m/s2.求:(已知:sin 37°=0.6,cos 37°=0.8) 在“用油膜法估测分子大小”的实验中,首先要确定一滴油酸酒精溶液中纯油酸的体积,具体做法是:把浓度为η的油酸酒精溶液一滴一滴地滴入量筒,记下滴入溶液滴数n时、量筒内增加的体积为V,则一滴溶液中纯油酸的体积为$\frac{Vη}{n}$;然后将一滴油酸酒精溶液滴入盛水的浅盘里,待水面稳定后,记下如图油酸分布图,已知图中每个正方形小方格的面积为S0.则油酸分子直径大小的表达式为$\frac{Vη}{57n{S}_{0}}$.
在“用油膜法估测分子大小”的实验中,首先要确定一滴油酸酒精溶液中纯油酸的体积,具体做法是:把浓度为η的油酸酒精溶液一滴一滴地滴入量筒,记下滴入溶液滴数n时、量筒内增加的体积为V,则一滴溶液中纯油酸的体积为$\frac{Vη}{n}$;然后将一滴油酸酒精溶液滴入盛水的浅盘里,待水面稳定后,记下如图油酸分布图,已知图中每个正方形小方格的面积为S0.则油酸分子直径大小的表达式为$\frac{Vη}{57n{S}_{0}}$.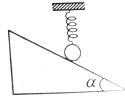 竖直弹簧的下端悬挂一小球,静止时,弹簧对小球的拉力大小为T.现使小球靠着倾角为α的光滑斜面,弹簧仍保持竖直,且整个装置处于静止状态,如图所示,则小球对斜面的压力大小为( )
竖直弹簧的下端悬挂一小球,静止时,弹簧对小球的拉力大小为T.现使小球靠着倾角为α的光滑斜面,弹簧仍保持竖直,且整个装置处于静止状态,如图所示,则小球对斜面的压力大小为( )