题目内容
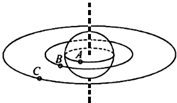
17. 一宇航员在半径为R、密度均匀的某星球表面,做如下实验,用不可伸长的长为l轻绳栓一质量为m的小球,上端固定在O点,如图所示,在最低点给小球某一初速度,使其绕O点恰好能在竖直面内做圆周运动,已知最高点速度为v0.引力常量为G,忽略各种阻力,求:
一宇航员在半径为R、密度均匀的某星球表面,做如下实验,用不可伸长的长为l轻绳栓一质量为m的小球,上端固定在O点,如图所示,在最低点给小球某一初速度,使其绕O点恰好能在竖直面内做圆周运动,已知最高点速度为v0.引力常量为G,忽略各种阻力,求:(1)该行星的平均密度ρ.
(2)该行星的第一宇宙速度v.
分析 (1)小球在最高点时重力恰好提供向心力,根据牛顿第二定律列式可以求解星球表面的重力加速度;最后根据密度的定义求解密度;
(2)行星的第一宇宙速度是星球表面卫星的环绕速度,根据重力等于万有引力列式求解即可.
解答 解:(1)设行星表面的重力加速度为g,对小球最高点,有:$mg=m\frac{{{v_0}^2}}{l}$
解得:g=$\frac{{{v_0}^2}}{l}$
对行星表面的物体m,有:$G\frac{Mm}{{R}^{2}}=mg$
故行星质量:M=$\frac{{{R^2}{v_0}^2}}{Gl}$
由于M=ρ•$\frac{4}{3}$πR3ρ,故行星的密度:
ρ=$\frac{{3{v_0}^2}}{4πGlR}$
(2)对处于行星表面附近做匀速圆周运动的卫星m,由牛顿第二定律,有:
mg=m$\frac{{v}^{2}}{R}$
故第一宇宙速度为:v=$\sqrt{\frac{{R{v_0}^2}}{l}}$;
答:(1)该行星的平均密度ρ为$\frac{{3{v_0}^2}}{4πGlR}$.
(2)该行星的第一宇宙速度v为$\sqrt{\frac{{R{v_0}^2}}{l}}$.
点评 对于卫星类问题,关键是明确卫星的动力学原理,根据牛顿第二定律列式求解;同时要记住星球表面重力等于万有引力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2. 我国在2015年年底发射首颗地球同步轨道高分辨率对地观测卫星高分四号.如图所示,A是静止在赤道上随地球自转的物体,B、C是同在赤道平面内的两颗人造卫星,B位于离地高度等于地球半径的圆形轨道上,C是高分四号卫星.则下列判断正确的是( )
我国在2015年年底发射首颗地球同步轨道高分辨率对地观测卫星高分四号.如图所示,A是静止在赤道上随地球自转的物体,B、C是同在赤道平面内的两颗人造卫星,B位于离地高度等于地球半径的圆形轨道上,C是高分四号卫星.则下列判断正确的是( )
 我国在2015年年底发射首颗地球同步轨道高分辨率对地观测卫星高分四号.如图所示,A是静止在赤道上随地球自转的物体,B、C是同在赤道平面内的两颗人造卫星,B位于离地高度等于地球半径的圆形轨道上,C是高分四号卫星.则下列判断正确的是( )
我国在2015年年底发射首颗地球同步轨道高分辨率对地观测卫星高分四号.如图所示,A是静止在赤道上随地球自转的物体,B、C是同在赤道平面内的两颗人造卫星,B位于离地高度等于地球半径的圆形轨道上,C是高分四号卫星.则下列判断正确的是( )| A. | 卫星B的线速度大于卫星C的线速度 | |
| B. | 物体A随地球自转的周期大于卫星C的周期 | |
| C. | 物体A随地球自转的加速度大于卫星C的加速度 | |
| D. | 物体A随地球自转的角速度大于卫星B的角速度 |
8.哈雷彗星绕太阳运动的轨道是比较扁的椭圆.下面说法中正确的是( )
| A. | 彗星在近日点的速率大于在远日点的速率 | |
| B. | 彗星在近日点的向心加速度大于在远日点的向心加速度 | |
| C. | 若彗星的周期为75年,则它的半长轴是地球公转半径的75倍 | |
| D. | 彗星在近日点的角速度大于在远日点的角速度 |
5.下面是地球、火星的有关情况比较的表格
已知万有引力常量G=6.67×10-11Nm2/kg2,根据以上信息,计算:
①地球与火星(行星的运动可看做圆周运动)万有引力的最大值?(结果保留两位有效数字)
②从某次万有引力最大值至下次万有引力最大之间的时间间隔?(结果保留两位有效数字)
| 星球 | 地球 | 火星 |
| 公转半径 | 1.5×108 km | 2.25×108 km |
| 自转周期 | 23h56min | 24h37min |
| 表面温度 | 15℃ | -100℃~0℃ |
| 公转周期 | 365d | 687d |
| 质量 | 6.0×1024kg | 6.4×1023kg |
①地球与火星(行星的运动可看做圆周运动)万有引力的最大值?(结果保留两位有效数字)
②从某次万有引力最大值至下次万有引力最大之间的时间间隔?(结果保留两位有效数字)
6. 如图所示,水平传送带由电动机带动,始终保持以速度v匀速运动,质量为m的物体在传送带上由静止释放,经过一段时间保持与传送带相对静止.物体与传送带之间的动摩擦因数为μ,在物体从静止释放到相对静止这一过程,物体相对于地的位移为x1、物体相对于传送带的位移为x2,传送带相对于地的位移为x3,下列说法正确的是( )
如图所示,水平传送带由电动机带动,始终保持以速度v匀速运动,质量为m的物体在传送带上由静止释放,经过一段时间保持与传送带相对静止.物体与传送带之间的动摩擦因数为μ,在物体从静止释放到相对静止这一过程,物体相对于地的位移为x1、物体相对于传送带的位移为x2,传送带相对于地的位移为x3,下列说法正确的是( )
 如图所示,水平传送带由电动机带动,始终保持以速度v匀速运动,质量为m的物体在传送带上由静止释放,经过一段时间保持与传送带相对静止.物体与传送带之间的动摩擦因数为μ,在物体从静止释放到相对静止这一过程,物体相对于地的位移为x1、物体相对于传送带的位移为x2,传送带相对于地的位移为x3,下列说法正确的是( )
如图所示,水平传送带由电动机带动,始终保持以速度v匀速运动,质量为m的物体在传送带上由静止释放,经过一段时间保持与传送带相对静止.物体与传送带之间的动摩擦因数为μ,在物体从静止释放到相对静止这一过程,物体相对于地的位移为x1、物体相对于传送带的位移为x2,传送带相对于地的位移为x3,下列说法正确的是( )| A. | 物体获得的动能Ek=μmgx1,物体与传送带之间摩擦热能Q=μmgx2 | |
| B. | 物体获得的动能Ek=μmgx2,物体与传送带之间摩擦热能Q=$\frac{1}{2}$mv2 | |
| C. | 电动机因为传送此物体需要多消耗的电能E=mv2=μmgx3 | |
| D. | 摩擦力对物体做的功W1=μmgx1,传送带克服摩擦力做的功W2=μmgx2 |
7.2015年12月29日0时04分,我国在西昌卫星发射中心成功发射高分四号卫星,至此我国航天发射“十二五”任务圆满收官,高官四号卫星是我国首颗地球同步轨道高分辨率光学成像卫星,也是目前世界上空间分辨率最高、幅宽最大的地球同步轨道卫星,它的发射和应用将显著提升我国对地遥感观测能力,该卫星在轨道正常运行时,下列说法正确的是( )
| A. | 卫星的轨道半径可以近似等于地球半径 | |
| B. | 卫星的线速度一定大于第一宇宙速度 | |
| C. | 卫星的向心加速度一定小于地球表面的重力加速度 | |
| D. | 卫星的运行周期一定大于月球绕地球运动的周期 |