题目内容
12.某太空探测器绕火星做匀速圆周运动,离火星表面的高度为h,环绕n圈所用时间为t,已知火星半径为R,求(1)该探测器的环绕线速度v;
(2)火星表面重力加速度g.
分析 (1)先求出周期T,由半径与周期可确定出线速度.
(2)由由万有引力等于重力可确定加速度g.
解答 解:(1)周期T=$\frac{t}{n}$ 则v=$\frac{2πr}{T}$=$\frac{2πn(R+h)}{t}$
(2)由万有引力等于向心力:$G\frac{Mm}{(R+h)^{2}}=m\frac{4{π}^{2}}{{T}^{2}}(R+h)$
又万有引力等于重力:$G\frac{Mm}{{R}^{2}}=mg$
可得:g=$\frac{4{π}^{2}(R+h)^{3}}{{T}^{2}{R}^{2}}$=$\frac{4{π}^{2}{n}^{2}(R+h)^{3}}{{n}^{2}{R}^{2}}$
答:(1)该探测器的环绕线速度为$\frac{2πn(R+h)}{t}$;
(2)火星表面重力加速度为$\frac{4{π}^{2}{n}^{2}(R+h)^{3}}{{n}^{2}{R}^{2}}$.
点评 明确线速度与周期的关系求得线速度,由万有引力提供向心力确定加速度.不难.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
17. 如图所示,高为H的塔吊臂上有一可以沿水平方向运动的小车A,小车A下的绳索吊着重物B.在小车A与物体B以相同的水平速度沿吊臂向右匀速运动的同时,绳索将重物B向上吊起,A、B之间的距离以d=H-t2规律随时间t变化,则在上述过程中( )
如图所示,高为H的塔吊臂上有一可以沿水平方向运动的小车A,小车A下的绳索吊着重物B.在小车A与物体B以相同的水平速度沿吊臂向右匀速运动的同时,绳索将重物B向上吊起,A、B之间的距离以d=H-t2规律随时间t变化,则在上述过程中( )
 如图所示,高为H的塔吊臂上有一可以沿水平方向运动的小车A,小车A下的绳索吊着重物B.在小车A与物体B以相同的水平速度沿吊臂向右匀速运动的同时,绳索将重物B向上吊起,A、B之间的距离以d=H-t2规律随时间t变化,则在上述过程中( )
如图所示,高为H的塔吊臂上有一可以沿水平方向运动的小车A,小车A下的绳索吊着重物B.在小车A与物体B以相同的水平速度沿吊臂向右匀速运动的同时,绳索将重物B向上吊起,A、B之间的距离以d=H-t2规律随时间t变化,则在上述过程中( )| A. | 绳索受到的拉力不断增大 | |
| B. | 绳索对重物做功的功率不断增大 | |
| C. | 重物做速度大小不断增大的曲线运动 | |
| D. | 重物做加速度大小不断减小的曲线运动 |
4.下面是金星、地球、火星的有关情况比较.
根据以上信息,关于地球及地球的两个邻居金星和火星(可看作匀速圆周运动),下列判断正确的是( )
| 星球 | 金星 | 地球 | 火星 |
| 公转半径 | 1.0×108km | 1.5×108km | 2.25×108km |
| 自转周期 | 243日 | 23时56分 | 24时37分 |
| 表面温度 | 480℃ | 15℃ | -100℃~0℃ |
| A. | 金星公转的线速度最小,火星公转的线速度最大 | |
| B. | 金星公转的向心加速度大于地球公转的向心加速度 | |
| C. | 金星的公转周期一定比地球的公转周期小 | |
| D. | 金星的公转角速度一定比地球的大 |
1.在物体运动过程中,下列说法正确的有( )
| A. | 动量不变的运动,一定是匀速运动? | |
| B. | 若某一个力对物体做功为零,则这个力对该物体的冲量也一定为零 | |
| C. | 如果在任何相等时间内物体所受的冲量相等(不为零),那么该物体一定做匀变速运动 | |
| D. | 动量大小不变的运动,可能是变速运动? |
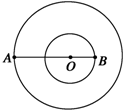 如图所示,双星系统中的星球A、B都可视为质点,A、B绕两者连线上的O点做匀速圆周运动,A、B之间距离不变,观测到A的速率为v、运行周期为T,二者质量分别为m1、m2.则B的周期为T;B的速率为$\frac{{m}_{1}^{\;}v}{{m}_{2}^{\;}}$(用题中物理量字母表示)
如图所示,双星系统中的星球A、B都可视为质点,A、B绕两者连线上的O点做匀速圆周运动,A、B之间距离不变,观测到A的速率为v、运行周期为T,二者质量分别为m1、m2.则B的周期为T;B的速率为$\frac{{m}_{1}^{\;}v}{{m}_{2}^{\;}}$(用题中物理量字母表示) 风洞飞行表演是一种高科技的惊险的娱乐节目.在某次表演中,假设风洞内向上的总风量和风速保持不变.质量为m的表演者通过调整身姿,可改变所受的向上的风力大小,以获得不同的运动效果.假设人体受风力大小与正对面积成正比,已知水平横躺时受风力面积最大,且人体站立时受风力面积为水平横躺时受风力面积的$\frac{1}{8}$,风洞内人体可上下移动的空间总高度AC=H.开始时,若人体与竖直方向成一定角度倾斜时,受风力有效面积是最大值的一半,恰好使表演者在最高点A点处于静止状态;后来,表演者从A点开始,先以向下的最大加速度匀加速下落,经过某处B点后,再以向上的最大加速度匀减速下落,刚好能在最低点C处减速为零,试求:
风洞飞行表演是一种高科技的惊险的娱乐节目.在某次表演中,假设风洞内向上的总风量和风速保持不变.质量为m的表演者通过调整身姿,可改变所受的向上的风力大小,以获得不同的运动效果.假设人体受风力大小与正对面积成正比,已知水平横躺时受风力面积最大,且人体站立时受风力面积为水平横躺时受风力面积的$\frac{1}{8}$,风洞内人体可上下移动的空间总高度AC=H.开始时,若人体与竖直方向成一定角度倾斜时,受风力有效面积是最大值的一半,恰好使表演者在最高点A点处于静止状态;后来,表演者从A点开始,先以向下的最大加速度匀加速下落,经过某处B点后,再以向上的最大加速度匀减速下落,刚好能在最低点C处减速为零,试求: 一宇航员在半径为R、密度均匀的某星球表面,做如下实验,用不可伸长的长为l轻绳栓一质量为m的小球,上端固定在O点,如图所示,在最低点给小球某一初速度,使其绕O点恰好能在竖直面内做圆周运动,已知最高点速度为v0.引力常量为G,忽略各种阻力,求:
一宇航员在半径为R、密度均匀的某星球表面,做如下实验,用不可伸长的长为l轻绳栓一质量为m的小球,上端固定在O点,如图所示,在最低点给小球某一初速度,使其绕O点恰好能在竖直面内做圆周运动,已知最高点速度为v0.引力常量为G,忽略各种阻力,求: