题目内容
4. 如图所示,用长为l的轻质细线将质量为m的小球悬挂于O点,细线能承受的最大拉力大小为7mg.小球在外力作用下静止于A处,此时细线偏离竖直方向的夹角为60°.撤去外力,让小球由静止释放,摆到最低点B时,细线被O点正下方的光滑小钉子挡住,钉子离O点的距离满足一定条件时,小球能继续运动且细线不松弛.不计空气阻力,重力加速度为g.求:
如图所示,用长为l的轻质细线将质量为m的小球悬挂于O点,细线能承受的最大拉力大小为7mg.小球在外力作用下静止于A处,此时细线偏离竖直方向的夹角为60°.撤去外力,让小球由静止释放,摆到最低点B时,细线被O点正下方的光滑小钉子挡住,钉子离O点的距离满足一定条件时,小球能继续运动且细线不松弛.不计空气阻力,重力加速度为g.求:(1)小球静止于A处时所受最小外力;
(2)小球运动过程中离A处位移的范围;
(3)钉子离O点距离应该满足的条件.
分析 (1)当外力与绳子方向垂直斜向上时,外力最小,根据共点力平衡求出最小外力.
(2)根据小球摆动的情况分析离A处位移的最大值,从而得出位移的范围.
(3)分析钉子离O点的距离需满足的情况:1、不越过四分之一圆周,2、越过圆周的最高点,3、在最低点拉力不超过7mg,根据牛顿第二定律、机械能守恒综合求解.
解答 解:(1)当外力与绳垂直斜向上时,外力最小,
由共点力平衡可得,F=mgsin60°=$\frac{\sqrt{3}}{2}mg$.
(2)钉子和O点重合时,当小球运动到左侧最高点时,位移最大,根据机械能守恒条件可知,小球运动到左侧最高点和初始位置等高,
根据几何关系知,小球运动过程中的最大位移${x}_{m}=2×l×\frac{\sqrt{3}}{2}=\sqrt{3}l$,
所以$0≤x≤\sqrt{3}l$.
(3)①当钉子与A点等高时,小球运动到最高点的速度为零,
${h}_{1}=\frac{l}{2}$,
②小球运动到最低点绳子恰好不断裂,设此时小球运动半径为r1,
根据牛顿第二定律得,$7mg-mg=m\frac{{{v}_{1}}^{2}}{{r}_{1}}$,
由机械能守恒定律得,mgl(1-cos60°)=$\frac{1}{2}m{{v}_{1}}^{2}$,
解得${r}_{1}=\frac{1}{6}l$,钉子距离O点的距离${l}_{1}=l-\frac{1}{6}l=\frac{5}{6}l$.
③小球绕过钉子又能运动到圆周的最高点,设此时小球运动的半径为r2,
由机械能守恒定律可得,$mg\frac{l}{2}-mg•2{r}_{2}=\frac{1}{2}m{{v}_{2}}^{2}$,
由牛顿第二定律得,$mg=m\frac{{{v}_{2}}^{2}}{{r}_{2}}$,
代入数据解得${r}_{2}=\frac{l}{5}$,钉子距离O点的距离${l}_{2}=l-\frac{l}{5}=\frac{4}{5}l$,
所以钉子离O点的距离h满足的条件$h<\frac{l}{2}$,$\frac{4}{5}l≤h≤\frac{5l}{6}$.
答:(1)小球静止于A处时所受最小外力为$\frac{\sqrt{3}}{2}mg$.
(2)小球运动过程中离A处位移的范围为$0≤x≤\sqrt{3}l$.
(3)钉子离O点距离应该满足的条件为$h<\frac{l}{2}$或$\frac{4}{5}l≤h≤\frac{5l}{6}$.
点评 本题综合考查了共点力平衡、牛顿第二定律、机械能守恒的综合运用,对于第三问,关键抓住临界情况,结合牛顿第二定律和机械能守恒进行求解,有一定的难度.

| A. | 该船可能垂直河岸横渡到对岸 | |
| B. | 当船头垂直河岸横渡时,过河所用的时间最10s | |
| C. | 当船头垂直河岸横渡时,船的位移最小是100m | |
| D. | 该船船头无论朝向哪个方向渡到对岸,船到对岸的位移都大于100m |
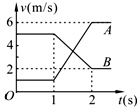
| A. | A、B的动量变化量一定相同 | |
| B. | A、B的质量之比为5:3 | |
| C. | A的动能增加量一定等于B的动能减少量 | |
| D. | A对B做多少负功,B对A就做多少正功 |
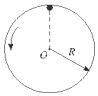 如图质量为m的小球在竖直平面内的光滑圆轨道上做圆周运动.圆半径为R,小球经过圆环最高点时刚好不脱离圆环,则通过最高点时( )
如图质量为m的小球在竖直平面内的光滑圆轨道上做圆周运动.圆半径为R,小球经过圆环最高点时刚好不脱离圆环,则通过最高点时( )| A. | 小球的线速度大小等于$\sqrt{gR}$ | B. | 小球的向心加速度大小等于g | ||
| C. | 小球对圆环的压力大小等于mg | D. | 小球受到的向心力等于重力mg |
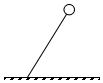 如图所示,在匀强电场中,绝缘丝线一端固定于地面,另一端系住一个带电小球,张紧的丝线使小球处于静止状态.忽略空气阻力,剪断丝线后小球将做( )
如图所示,在匀强电场中,绝缘丝线一端固定于地面,另一端系住一个带电小球,张紧的丝线使小球处于静止状态.忽略空气阻力,剪断丝线后小球将做( )| A. | 类平抛运动 | B. | 匀速圆周运动 | C. | 匀加速直线运动 | D. | 变加速曲线运动 |
| A. | 3m | B. | 4m | C. | 5m | D. | 6m |
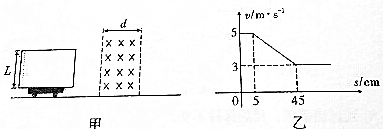
 如图所示,水平面上固定着距离L的两根光滑平行金属导轨,导轨间有竖直方向的匀强磁场,导轨电阻不计,另有两根长为L的金属棒AB和CD垂直导轨放置,水平恒力F拉着AB向右运动时,CD也会跟着向右运动,AB和CD的电阻分别是R1和R2,质量分别是m1和m2,当金属棒中电流强度恒定时,求两金属棒的速度差△v.
如图所示,水平面上固定着距离L的两根光滑平行金属导轨,导轨间有竖直方向的匀强磁场,导轨电阻不计,另有两根长为L的金属棒AB和CD垂直导轨放置,水平恒力F拉着AB向右运动时,CD也会跟着向右运动,AB和CD的电阻分别是R1和R2,质量分别是m1和m2,当金属棒中电流强度恒定时,求两金属棒的速度差△v.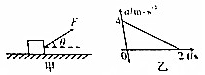 如图甲所示,质量为0.6kg的物块静止在水平面上,物块与水平面间的动摩擦因数为$\frac{1}{3}$,t=0时刻给物块一个与水平方向成θ=37°,斜向右上方的拉力,使物块向右运动,其加速度随时间变化的关系图象如图乙所示,重力加速度为g=10m/s2,sin37°=0.6,cos37°=0.8,求:
如图甲所示,质量为0.6kg的物块静止在水平面上,物块与水平面间的动摩擦因数为$\frac{1}{3}$,t=0时刻给物块一个与水平方向成θ=37°,斜向右上方的拉力,使物块向右运动,其加速度随时间变化的关系图象如图乙所示,重力加速度为g=10m/s2,sin37°=0.6,cos37°=0.8,求: