题目内容
18.如图甲,一个倾角为30°的光滑斜面的底端固定一个与斜面垂直的挡板,劲度系数k=0.1N/cm的轻质弹簧一端与挡板固定,另一端与一个质量为m=0.2kg、带电量为+2×10-7C的小滑块固定,现将滑块压到距挡板为L=30cm的A点由静止释放,滑块刚好能在A、B做简谐运动,其位移-时间图如图乙所示,求:(1)该滑块做间谐运动的振动方程;
(2)弹簧的原长L0;
(3)若在滑块到达A点时加一个竖直向下、大小为E=2×106C的匀强电场,滑块还能继续做简谐运动吗?若能,试求出振幅A′.
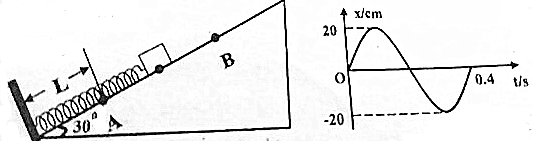
分析 (1)由图读出滑块的振幅与周期,结合振动方程中的物理量特点,即可写出振动方程;
(2)根据题意与位移-时间图,判断出滑块在平衡位置处对应的弹簧的形变量,结合胡克定律即可求出弹簧的原长;
(3)当加电场后,对滑块进行受力分析即可求出.
解答 解:(1)由图可知,该振子的振幅为20cm=0.2m,周期为0.4s,所以圆频率:$ω=\frac{2π}{T}=\frac{2π}{0.4}=5π$
所以,该滑块做间谐运动的振动方程为:x=Asinωt=0.2sin5πt (m)
(2)滑块在平衡位置处受到的弹簧的弹力与重力沿斜面向下的分力是相等的,设此时弹簧的压缩量为x,所以:
mgsin30°=kx
k=0.1N/cm=10N/m
代入数据得:x=0.1m=10cm
所以弹簧的原长:L0=L+A+x=30cm+20cm+10cm=60cm
(3)在A点时弹簧的压缩量:△x=x+A=10cm+20cm=30cm=0.3m
选取沿斜面向上为正方向,则加电场后,滑块在A点的受力沿斜面方向的分力:
F合斜面=k△x-mgsin30°-qEsin30°=10×0.3-0.2×10×0.5-2×10-7×2×106=1.6N
可知在A点滑块受到沿斜面向上的合外力为1.6N,所以滑块将从A点开始 向上做加速运动,由于电场力是恒力,所以滑块仍然可以做简谐振动.
此时设合外力等于0时弹簧的压缩量为x′,则:0=kx′-mgsin30°-qEsin30°
代入数据得:x=0.14m=14cm
所以此时滑块的振幅为:A′=A+x-x′=0.2m+0.1m-0.14m=0.16m=16cm
答:(1)该滑块做间谐运动的振动方程为x=Asinωt=0.2sin5πt (m);
(2)弹簧的原长为60cm;
(3)若在滑块到达A点时加一个竖直向下、大小为E=2×106C的匀强电场,滑块还能继续做简谐运动,此时的振幅A′为16cm.
点评 该题基于简谐振动模型考查胡克定律、共点力平衡等知识点的内容,题目的设计思路新颖,涉及知识点多,公式多,在解答的过程中要注意对各个过程以及状态的分析.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案| A. | 牛顿通过实验发现了引力常量 | |
| B. | 曲线运动一定是变速运动 | |
| C. | 第一宇宙速度是环绕地球所有卫星中最大的运行速度 | |
| D. | 人造卫星的轨道可以在北半球的上空与某一纬线重合 |
| A. | 原子核的结合能等于使其完全分解成自由核子释放的能量 | |
| B. | 一重原子核衰变成α粒子和另一原子核,衰变产物的结合能之和一定大于原来重核的结合能 | |
| C. | 核子结合成原子核时会出现质量亏损,亏损的质量转化为释放的能量 | |
| D. | 只有入射光的波长大于金属的极限波长时,光电效应才能产生 |
| A. | 由p=$\frac{W}{t}$知,只要知道W和t就可求出任意时刻的功率 | |
| B. | 由P=Fv既能求某一时刻的瞬时功率,也可以求出平均功率 | |
| C. | 由P=Fv知,随着汽车速度的增大,它的功率也可以无限制地增大 | |
| D. | 由P=Fv知,当汽车发动机功率一定时,牵引力与速度成反比 |
 在如图1所示的装置中,矩形线圈匝数N=100匝,线圈电阻内阻r=3Ω,L1=1m,L2=2m,电阻R=3Ω,磁感应强度按图2做周期性变化,板间距为d=0.5m,长为l=1.05m的平行板电容器,在t=0.05s时,有电荷量q=1.6×10-10c,质量m=3.2×10-9kg的正离子从距上极板0.2m处以水平速度vo=1m/s飞入平行板,不计重力.求:
在如图1所示的装置中,矩形线圈匝数N=100匝,线圈电阻内阻r=3Ω,L1=1m,L2=2m,电阻R=3Ω,磁感应强度按图2做周期性变化,板间距为d=0.5m,长为l=1.05m的平行板电容器,在t=0.05s时,有电荷量q=1.6×10-10c,质量m=3.2×10-9kg的正离子从距上极板0.2m处以水平速度vo=1m/s飞入平行板,不计重力.求: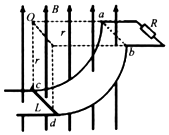 如图所示,两根等高光滑的$\frac{1}{4}$圆弧轨道,半径为r、间距为L,轨道电阻不计.在轨道顶端连有一阻值为R的电阻,整个装置处在一竖直向上的匀强磁场中,磁感应强度为B.现有一根长度稍大于L、电阻为$\frac{R}{2}$,质量为m的金属棒从轨道最低位置cd开始,以初速度v0自行滑向轨道,最后刚好能运动到ab处,重力加速度为g,求:
如图所示,两根等高光滑的$\frac{1}{4}$圆弧轨道,半径为r、间距为L,轨道电阻不计.在轨道顶端连有一阻值为R的电阻,整个装置处在一竖直向上的匀强磁场中,磁感应强度为B.现有一根长度稍大于L、电阻为$\frac{R}{2}$,质量为m的金属棒从轨道最低位置cd开始,以初速度v0自行滑向轨道,最后刚好能运动到ab处,重力加速度为g,求: 某实验小组的同学利用落体法验证机械能守恒定律,实验装置如图甲所示,该小组的同学完成了如下的操作:
某实验小组的同学利用落体法验证机械能守恒定律,实验装置如图甲所示,该小组的同学完成了如下的操作: 如图所示,一个边长L=10cm,匝数N=100匝的正方形线圈abcd在匀强磁场中绕垂直于磁感线的对称轴OO′匀速转动,磁感应强度B=0.50T,角速度ω=10πrad/s,外电路电阻R=4.0Ω,线圈内阻r=1.0Ω.
如图所示,一个边长L=10cm,匝数N=100匝的正方形线圈abcd在匀强磁场中绕垂直于磁感线的对称轴OO′匀速转动,磁感应强度B=0.50T,角速度ω=10πrad/s,外电路电阻R=4.0Ω,线圈内阻r=1.0Ω. 如图所示,质量为M的物块钩在水平放置的左端固定的轻质弹簧的右端,构成一弹簧振子,物块可沿光滑水平面在BC间做简谐运动,振幅为A.在运动过程中将一质量为m的小物块轻轻地放在M上,第一次是当M运动到平衡位置O处时放在上面,第二次是当M运动到最大位移处C处时放在上面,观察到第一次放后的振幅为A1,第二次放后的振幅为A2,则( )
如图所示,质量为M的物块钩在水平放置的左端固定的轻质弹簧的右端,构成一弹簧振子,物块可沿光滑水平面在BC间做简谐运动,振幅为A.在运动过程中将一质量为m的小物块轻轻地放在M上,第一次是当M运动到平衡位置O处时放在上面,第二次是当M运动到最大位移处C处时放在上面,观察到第一次放后的振幅为A1,第二次放后的振幅为A2,则( )