题目内容
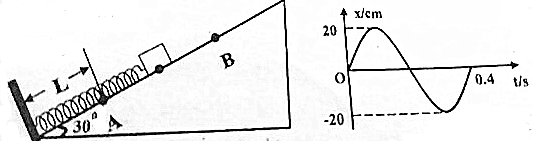
6. 在如图1所示的装置中,矩形线圈匝数N=100匝,线圈电阻内阻r=3Ω,L1=1m,L2=2m,电阻R=3Ω,磁感应强度按图2做周期性变化,板间距为d=0.5m,长为l=1.05m的平行板电容器,在t=0.05s时,有电荷量q=1.6×10-10c,质量m=3.2×10-9kg的正离子从距上极板0.2m处以水平速度vo=1m/s飞入平行板,不计重力.求:
在如图1所示的装置中,矩形线圈匝数N=100匝,线圈电阻内阻r=3Ω,L1=1m,L2=2m,电阻R=3Ω,磁感应强度按图2做周期性变化,板间距为d=0.5m,长为l=1.05m的平行板电容器,在t=0.05s时,有电荷量q=1.6×10-10c,质量m=3.2×10-9kg的正离子从距上极板0.2m处以水平速度vo=1m/s飞入平行板,不计重力.求:(1)t=0.05s时,平行板间的电压大小?
(2)当离子飞出平行板时,电场力对离子所做的功?
分析 (1)由楞次定律求得电动势,在由串联电路原理根据欧姆定律求得路端电压;
(2)根据路端电压求得电场力、离子在竖直方向上的速度随时间的变化;再由几何关系求得离子运动时间,然后对离子分段求取电场力做的功,累加即可.
解答 解:(1)在t=0.05s时,由于磁场变化,应用楞次定律可得:线圈产生的感应电动势为:
${E_1}=\frac{N△Φ}{△t}=\frac{{N△B{L_1}{L_2}}}{△t}=200V$;
由电路知识可知,对整个回路有:$I=\frac{E_1}{r+R}$
电阻两端电压为:U=IR=100V;
因为平行板电容器与R并联,故其两端电压为100V;
(2)两平行板间电场强度为:
${E_2}=\frac{U}{d}=200V/m$;
离子进入电场后水平方向做匀速,竖直方向做周期性匀变速直线运动(如图) ,
,
所以,离子不可能打在上级板上,且其在一个周期内的位移为0.2m;
因为离子水平方向做匀速运动,所以,离子若不与极板碰撞,则在平行板间运动的时间为:
$t=\frac{l}{v_0}=1.05s$;
因为粒子进入电场时距离下级板的距离为0.3m,所以,离子将打在下极板上.
粒子在t=0.15s时,位移为0.025m(正向最大),没有接触到上级板;
粒子在t=0.55s时,位移为-0.175m;
则当位移为-0.3m时有:$t=0.85-0.1\sqrt{2}(s)$;
$a=\frac{{q{E_2}}}{m}=10m/{s^2}$;F=ma=3.2×10-8N,粒子受力如图所示 ;
;
又有粒子在一个周期内F为正时与F为负时的位移相同,所以,一个周期内电场力对离子做功为零,
所以,若无下边界,则离子在0.85s时电场力对离子所做的功为:
${W}_{0.85}=3.2×1{0}^{-8}×0.025J+0+0=8×1{0}^{-10}J$;
在$0.85-0.1\sqrt{2}(s)$到0.85s过程中,电场力对粒子所做的功为:
$W′=3.2×1{0}^{-8}×[-\frac{1}{2}×10×(0.1\sqrt{2})^{2}]J=-3.2×1{0}^{-9}J$
所以,粒子在穿越电场的过程中,电场力对粒子所做的功为:
$W={W}_{0.85}-W'=4×1{0}^{-9}J$;
答:(1)t=0.05s时,平行板间的电压大小为100V;
(2)当离子飞出平行板时,电场力对离子所做的功为4×10-9J.
点评 在求解粒子运动问题,一定要考虑电磁场的边界对粒子运动的影响,根据边界条件得到粒子运动时间,进而求得速度、场强、磁感应强度等问题.

| A. | 一定等于7.9 km/s | |
| B. | 一定小于7.9 km/s | |
| C. | 大于或等于7.9 km/s,而小于11.2 km/s | |
| D. | 只需大于7.9 km/s |
| A. | $\sqrt{\frac{M{g}^{3}}{ρs}}$ | B. | $\frac{1}{2}$$\sqrt{\frac{M{g}^{3}}{ρs}}$ | C. | ρs($\sqrt{\frac{Mg}{ρs}}$)3 | D. | $\frac{ρs}{2}$($\sqrt{\frac{Mg}{ρs}}$)3 |

| A. | 卫星在此段轨道上动能一直减小 | B. | 卫星经过P点时动能最大 | ||
| C. | 卫星经过P点时加速度为0 | D. | 卫星经过P点时速度方向由P指向A |
| A. | 哑铃 | B. | 单杠 | C. | 弹簧拉力器 | D. | 以上都不行 |
| A. | PM2.5的尺寸与空气中氧分子的尺寸的数量级相当 | |
| B. | PM2.5在空气中的运动属于分子热运动 | |
| C. | PM2.5的运动轨迹是由气流的运动决定的 | |
| D. | PM2.5必然有内能 |