题目内容
3. 平抛运动任意时刻速度的方向与水平方向的夹角定义为速度的偏向角,某物体做平抛运动的时间与速度偏向角正切值之间函数关系如图所示,g取10m/s2,则下列说法中正确的是( )
平抛运动任意时刻速度的方向与水平方向的夹角定义为速度的偏向角,某物体做平抛运动的时间与速度偏向角正切值之间函数关系如图所示,g取10m/s2,则下列说法中正确的是( )| A. | 1s末物体的速度大小为$5\sqrt{5}$m/s | |
| B. | 平抛的初速度大小为20m/s | |
| C. | 第1s内物体的位移大小为$\sqrt{5}$m | |
| D. | 第1s内物体位移的方向与水平方向夹角的正切值为1 |
分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,结合运动学公式求出时间t的表达式,通过表达式,结合图线的斜率分析求解.
解答 解:B、平抛运动速度偏向角的正切值$tanθ=\frac{{v}_{y}^{\;}}{{v}_{0}^{\;}}=\frac{gt}{{v}_{0}^{\;}}$,所以t=$\frac{{v}_{0}^{\;}tanθ}{g}$,即图象斜率为k=$k=\frac{{v}_{0}^{\;}}{g}$,所以${v}_{0}^{\;}=kg=\frac{y}{x}g=\frac{1}{2}×10=5m/s$,故B错误;
A、1S末的竖直速度大小为${v}_{y}^{\;}=gt=10×1=10m/s$,1s末物体的速度大小$v=\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}=\sqrt{{5}_{\;}^{2}+1{0}_{\;}^{2}}=5\sqrt{5}m/s$,故A正确;
C、由平抛运动规律可知,第1s内水平位移$x={v}_{0}^{\;}t=5×1=5m$
竖直位移$y=\frac{1}{2}g{t}_{\;}^{2}=\frac{1}{2}×10×{1}_{\;}^{2}=5m$,第1s内位移大小$l=\sqrt{{x}_{\;}^{2}+{y}_{\;}^{2}}=\sqrt{{5}_{\;}^{2}+{5}_{\;}^{2}}m=5\sqrt{2}m$,故C错误;
D、第1s内位移与水平方向夹角的正切值$tanθ=\frac{y}{x}=\frac{5}{5}=1$,故D正确.
故选:AD.
点评 考查学生对平抛运动规律的理解和掌握及应用图象解决物理问题的能力.知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式和平行四边形定则进行求解.

 如图所示,在点电荷Q产生的电场中,试探电荷q只在电场力作用下沿椭圆轨道运动.已知Q位于椭圆轨道的一个焦点上,则关于试探电荷q的说法正确的是( )
如图所示,在点电荷Q产生的电场中,试探电荷q只在电场力作用下沿椭圆轨道运动.已知Q位于椭圆轨道的一个焦点上,则关于试探电荷q的说法正确的是( )| A. | 从M点运动到N点的过程中电势能增加 | |
| B. | 从M点运动到N点的过程中动能增加 | |
| C. | q在M点的加速度比N点的加速度大 | |
| D. | 从M点运动到N点,电势能与动能之和不变 |
 把质量为m的小球(可看作质点)放在竖直的轻质弹簧上,并把小球向下按到A的位置(图甲),如图所示.迅速松手后,弹簧把小球弹起,球升至最高位置C点(图丙),途中经过位置B时弹簧正好处于自由状态(图乙).已知AB的高度差为h1,BC的高度差为h2,通过AB和BC所用时间为t1和t2,重力加速度为g,不计空气阻力( )
把质量为m的小球(可看作质点)放在竖直的轻质弹簧上,并把小球向下按到A的位置(图甲),如图所示.迅速松手后,弹簧把小球弹起,球升至最高位置C点(图丙),途中经过位置B时弹簧正好处于自由状态(图乙).已知AB的高度差为h1,BC的高度差为h2,通过AB和BC所用时间为t1和t2,重力加速度为g,不计空气阻力( )| A. | 小球从A上升到B位置的过程中,动能一直增大 | |
| B. | 小球从A上升到C位置的过程中,机械能先增大后不变 | |
| C. | 小球在图甲中时,弹簧的弹性势能为mg(h1+h2) | |
| D. | 若h1等于h2,则一定有t1小于t2 |
| A. | 释放相邻两个小球的时间间隔为T=5s | |
| B. | 第三个球与第六个球之间的距离为25m | |
| C. | 第一个球落地瞬间速度为50m/s | |
| D. | 从一号球到六号球顺序,连续相邻两球之间的距离之比为1:3:5:7:9 |

| A. | 在第1秒末加速度方向发生了改变 | B. | 第3秒末和第5秒末的位置相同 | ||
| C. | 在第1秒末速度方向发生了改变 | D. | 在前2秒内发生的位移为零 |
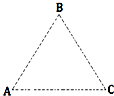 如图所示A、B、C是平行纸面的匀强电场中的三点,它们之间的距离均为L=2cm,电荷量为q=-1.0×10-5 C的电荷由A移动到C电场力做功W1=4.0×10-5 J,该电荷由C移动到B电场力做功W2=-2.0×10-5 J,若B点电势为零,由以上条件可知:A点的电势为-2V,场强的大小为200V/m,场强的方向为C指向A.
如图所示A、B、C是平行纸面的匀强电场中的三点,它们之间的距离均为L=2cm,电荷量为q=-1.0×10-5 C的电荷由A移动到C电场力做功W1=4.0×10-5 J,该电荷由C移动到B电场力做功W2=-2.0×10-5 J,若B点电势为零,由以上条件可知:A点的电势为-2V,场强的大小为200V/m,场强的方向为C指向A.
 如图所示,半径为R的半圆形玻璃砖水平放置,竖直的光屏紧挨玻璃砖.一束红光沿半径方向射向玻璃砖的圆心O,当红光在玻璃砖平面O点的入射角θ=30°时,光屏上会出现两个红色光斑,当入射角θ=45°时,光屏上恰好只剩一个红色光斑,不考虑光的多次反射.求:
如图所示,半径为R的半圆形玻璃砖水平放置,竖直的光屏紧挨玻璃砖.一束红光沿半径方向射向玻璃砖的圆心O,当红光在玻璃砖平面O点的入射角θ=30°时,光屏上会出现两个红色光斑,当入射角θ=45°时,光屏上恰好只剩一个红色光斑,不考虑光的多次反射.求: