题目内容
13.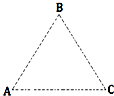 如图所示A、B、C是平行纸面的匀强电场中的三点,它们之间的距离均为L=2cm,电荷量为q=-1.0×10-5 C的电荷由A移动到C电场力做功W1=4.0×10-5 J,该电荷由C移动到B电场力做功W2=-2.0×10-5 J,若B点电势为零,由以上条件可知:A点的电势为-2V,场强的大小为200V/m,场强的方向为C指向A.
如图所示A、B、C是平行纸面的匀强电场中的三点,它们之间的距离均为L=2cm,电荷量为q=-1.0×10-5 C的电荷由A移动到C电场力做功W1=4.0×10-5 J,该电荷由C移动到B电场力做功W2=-2.0×10-5 J,若B点电势为零,由以上条件可知:A点的电势为-2V,场强的大小为200V/m,场强的方向为C指向A.
分析 根据试探电荷的电荷量和电场力做功,根据公式U=$\frac{W}{q}$分别求出A与无穷远间、A与B间电势差,无穷远处电势为零,再确定A、B两点的电势.再由U=Ed确定电场强度的大小和方向.
解答  解:对于C、B间电势差为UCB=$\frac{{W}_{CB}}{q}$=$\frac{-2×1{0}^{-5}}{-1×1{0}^{-5}}$V=2V,
解:对于C、B间电势差为UCB=$\frac{{W}_{CB}}{q}$=$\frac{-2×1{0}^{-5}}{-1×1{0}^{-5}}$V=2V,
若B点电势为零,UCB=φC-φB,则C点电势φC=2V.
而A与C间的电势差为UAC=$\frac{{W}_{AC}}{q}$=$\frac{4.0×1{0}^{-5}}{-1.0×1{0}^{-5}}$V=-4V,
UAC=φA-φC,则A点电势φA=-2V.
由上分析可知,AC连线的中点M电势为0,M与B点的连线即为等势线,且电场线垂直于等势线,三角形ABC为等边三角形,BM⊥AC,
根据沿着电场线方向,电势降低,则有匀强电场的方向由C到A;
则根据U=Ed可知,E=$\frac{{U}_{CA}}{L}$=$\frac{4}{0.02}$=200V/m
故答案为:-2;200;C指向A
点评 本题考查对电势差公式的应用能力,要注意在U=$\frac{W}{q}$应用时,各量均需代入符号,同时还要明确各物理量的符号的意义.

练习册系列答案
相关题目
12. 如图所示,实线是电场线,方向已标明,虚线ab是某一带电粒子(不计重力)在电场中的运动轨迹,根据以上条件可以做出的正确判断是( )
如图所示,实线是电场线,方向已标明,虚线ab是某一带电粒子(不计重力)在电场中的运动轨迹,根据以上条件可以做出的正确判断是( )
 如图所示,实线是电场线,方向已标明,虚线ab是某一带电粒子(不计重力)在电场中的运动轨迹,根据以上条件可以做出的正确判断是( )
如图所示,实线是电场线,方向已标明,虚线ab是某一带电粒子(不计重力)在电场中的运动轨迹,根据以上条件可以做出的正确判断是( )| A. | 粒子带负电 | B. | 粒子在a点的速度较大 | ||
| C. | 粒子在a点的加速度较大 | D. | 粒子在a点的电势能较大 |
4. 一边长为L、电阻为R的正方形单匝线框沿光滑水平面运动,以速度v1开始进入一磁感应强度为B的有界匀强磁场区域,最终以速度v2滑出磁场.设线框在运动过程中速度方向始终与磁场边界垂直,磁场的宽度大于L(如图所示).刚进入磁场瞬时,线框中的感应电流为I1.下列说法正确的是( )
一边长为L、电阻为R的正方形单匝线框沿光滑水平面运动,以速度v1开始进入一磁感应强度为B的有界匀强磁场区域,最终以速度v2滑出磁场.设线框在运动过程中速度方向始终与磁场边界垂直,磁场的宽度大于L(如图所示).刚进入磁场瞬时,线框中的感应电流为I1.下列说法正确的是( )
 一边长为L、电阻为R的正方形单匝线框沿光滑水平面运动,以速度v1开始进入一磁感应强度为B的有界匀强磁场区域,最终以速度v2滑出磁场.设线框在运动过程中速度方向始终与磁场边界垂直,磁场的宽度大于L(如图所示).刚进入磁场瞬时,线框中的感应电流为I1.下列说法正确的是( )
一边长为L、电阻为R的正方形单匝线框沿光滑水平面运动,以速度v1开始进入一磁感应强度为B的有界匀强磁场区域,最终以速度v2滑出磁场.设线框在运动过程中速度方向始终与磁场边界垂直,磁场的宽度大于L(如图所示).刚进入磁场瞬时,线框中的感应电流为I1.下列说法正确的是( )| A. | 线框完全在磁场中时的运动速度v=$\frac{{{v_1}-{v_2}}}{2}$ | |
| B. | 线框滑出磁场时的电流I2=$\frac{{{v_1}{I_1}}}{v_2}$ | |
| C. | 进入磁场的过程中,通过线框的电量q=$\frac{{L{I_1}}}{v_1}$ | |
| D. | 整个穿越磁场的过程中通过线框的总电量Q=$\frac{{B{L^2}}}{R}$ |
5. 如图所示的直角坐标系中,两电荷量分别为Q(Q>0)和-Q的点电荷对称地放置在x轴上原点O的两侧,a点位于x轴上O点与点电荷Q之间,b位于y轴O点上方,取无穷远处的电势为零.下列说法正确的是( )
如图所示的直角坐标系中,两电荷量分别为Q(Q>0)和-Q的点电荷对称地放置在x轴上原点O的两侧,a点位于x轴上O点与点电荷Q之间,b位于y轴O点上方,取无穷远处的电势为零.下列说法正确的是( )
 如图所示的直角坐标系中,两电荷量分别为Q(Q>0)和-Q的点电荷对称地放置在x轴上原点O的两侧,a点位于x轴上O点与点电荷Q之间,b位于y轴O点上方,取无穷远处的电势为零.下列说法正确的是( )
如图所示的直角坐标系中,两电荷量分别为Q(Q>0)和-Q的点电荷对称地放置在x轴上原点O的两侧,a点位于x轴上O点与点电荷Q之间,b位于y轴O点上方,取无穷远处的电势为零.下列说法正确的是( )| A. | b点的电势为零,电场强度也为零 | |
| B. | 正的试探电荷在a点的电势能大于零,所受电场力方向向右 | |
| C. | 将正的试探电荷从O点移到a点,电势能减少 | |
| D. | 将同一正的试探电荷先后分别从O、b点移到a点,第二次电势能的变化较大 |
2. a、b、c、d分别是一个菱形的四个顶点,∠abc=120°.现将三个等量的负点电荷-Q固定在a、b、c三个顶点上,将一个电量为+q的检验电荷依次放在菱形中心点O点和另一个顶点d处,则两点相比( )
a、b、c、d分别是一个菱形的四个顶点,∠abc=120°.现将三个等量的负点电荷-Q固定在a、b、c三个顶点上,将一个电量为+q的检验电荷依次放在菱形中心点O点和另一个顶点d处,则两点相比( )
 a、b、c、d分别是一个菱形的四个顶点,∠abc=120°.现将三个等量的负点电荷-Q固定在a、b、c三个顶点上,将一个电量为+q的检验电荷依次放在菱形中心点O点和另一个顶点d处,则两点相比( )
a、b、c、d分别是一个菱形的四个顶点,∠abc=120°.现将三个等量的负点电荷-Q固定在a、b、c三个顶点上,将一个电量为+q的检验电荷依次放在菱形中心点O点和另一个顶点d处,则两点相比( )| A. | +q在d点所受的电场力比在O点的大 | |
| B. | +q在d点所具有的电势能比在O点的大 | |
| C. | d点的电场强度小于O点的电场强度 | |
| D. | d点的电势低于O点的电势 |
3. 平抛运动任意时刻速度的方向与水平方向的夹角定义为速度的偏向角,某物体做平抛运动的时间与速度偏向角正切值之间函数关系如图所示,g取10m/s2,则下列说法中正确的是( )
平抛运动任意时刻速度的方向与水平方向的夹角定义为速度的偏向角,某物体做平抛运动的时间与速度偏向角正切值之间函数关系如图所示,g取10m/s2,则下列说法中正确的是( )
 平抛运动任意时刻速度的方向与水平方向的夹角定义为速度的偏向角,某物体做平抛运动的时间与速度偏向角正切值之间函数关系如图所示,g取10m/s2,则下列说法中正确的是( )
平抛运动任意时刻速度的方向与水平方向的夹角定义为速度的偏向角,某物体做平抛运动的时间与速度偏向角正切值之间函数关系如图所示,g取10m/s2,则下列说法中正确的是( )| A. | 1s末物体的速度大小为$5\sqrt{5}$m/s | |
| B. | 平抛的初速度大小为20m/s | |
| C. | 第1s内物体的位移大小为$\sqrt{5}$m | |
| D. | 第1s内物体位移的方向与水平方向夹角的正切值为1 |
 如图甲所示,两根足够长的光滑平行金属导轨相距l=0.4 m,导轨平面与水平面成θ=30°角,下端通过导线连接阻值R=0.5Ω的电阻.金属棒ab阻值r=0.3Ω,质量m=0.2kg,放在两导轨上,与导轨垂直并保持良好接触.其余部分电阻不计,整个装置处于垂直导轨平面向上的匀强磁场中.取g=10 m/s2.
如图甲所示,两根足够长的光滑平行金属导轨相距l=0.4 m,导轨平面与水平面成θ=30°角,下端通过导线连接阻值R=0.5Ω的电阻.金属棒ab阻值r=0.3Ω,质量m=0.2kg,放在两导轨上,与导轨垂直并保持良好接触.其余部分电阻不计,整个装置处于垂直导轨平面向上的匀强磁场中.取g=10 m/s2.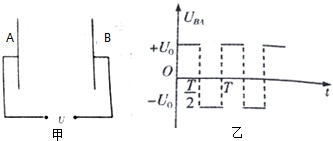
 如图所示,A、B两小球用等长的绝缘细线悬挂在支架上,A球带电3×10-6C的正电荷,B球带等量的负电荷,两悬点相距3cm,在外加匀强电场作用下,两球都在各自悬点正下方处于平衡状态,求该场强的大小和方向.(已知静电力常量为9.0×109N•m2/C2)
如图所示,A、B两小球用等长的绝缘细线悬挂在支架上,A球带电3×10-6C的正电荷,B球带等量的负电荷,两悬点相距3cm,在外加匀强电场作用下,两球都在各自悬点正下方处于平衡状态,求该场强的大小和方向.(已知静电力常量为9.0×109N•m2/C2)