题目内容
18. 如图所示,半径为R的半圆形玻璃砖水平放置,竖直的光屏紧挨玻璃砖.一束红光沿半径方向射向玻璃砖的圆心O,当红光在玻璃砖平面O点的入射角θ=30°时,光屏上会出现两个红色光斑,当入射角θ=45°时,光屏上恰好只剩一个红色光斑,不考虑光的多次反射.求:
如图所示,半径为R的半圆形玻璃砖水平放置,竖直的光屏紧挨玻璃砖.一束红光沿半径方向射向玻璃砖的圆心O,当红光在玻璃砖平面O点的入射角θ=30°时,光屏上会出现两个红色光斑,当入射角θ=45°时,光屏上恰好只剩一个红色光斑,不考虑光的多次反射.求:(1)玻璃砖的折射率;
(2)当入射角θ=30°时两光斑间的距离.
分析 (1)两光斑是由于光的反射和折射分别形成的,光屏上两个光斑恰好变为一个时,光线恰好在AB面恰好发生发全反射.根据临界角公式求解玻璃砖的折射率.
(2)当入射角θ=30°时,光线在AB同时发生反射和折射,反射光线沿半径射出到P点,由几何知识求得AP的长度.结合折射定律和几何知识求得AQ的长度,从而得到两光斑间的距离.
解答  解:(1)光屏上恰好只剩一个红色光斑,光线恰好在AB面恰好发生发全反射.由题可知,临界角 C=45°
解:(1)光屏上恰好只剩一个红色光斑,光线恰好在AB面恰好发生发全反射.由题可知,临界角 C=45°
则由sinC=$\frac{1}{n}$得:
n=$\frac{1}{sinC}$=$\frac{1}{sin45°}$=$\sqrt{2}$
(2)当入射角θ=30°时,光线在AB同时发生反射和折射,反射光线沿半径射出到P点,由反射定律和几何关系得:α=θ=30°
可得:AP=Rcotα=$\sqrt{3}$R
在AB发生折射,由n=$\frac{sinβ}{sinθ}$
解得:sinβ=$\frac{\sqrt{2}}{2}$,β=45°
可得 AQ=R
则两光斑间的距离为:PQ=AP+AQ=($\sqrt{3}$+1)R
答:
(1)玻璃砖的折射率是$\sqrt{2}$;
(2)当入射角θ=30°时两光斑间的距离是($\sqrt{3}$+1)R.
点评 对于几何光学问题,关键要正确作出光路图,运用折射定律和几何知识结合进行处理.

练习册系列答案
相关题目
3. 平抛运动任意时刻速度的方向与水平方向的夹角定义为速度的偏向角,某物体做平抛运动的时间与速度偏向角正切值之间函数关系如图所示,g取10m/s2,则下列说法中正确的是( )
平抛运动任意时刻速度的方向与水平方向的夹角定义为速度的偏向角,某物体做平抛运动的时间与速度偏向角正切值之间函数关系如图所示,g取10m/s2,则下列说法中正确的是( )
 平抛运动任意时刻速度的方向与水平方向的夹角定义为速度的偏向角,某物体做平抛运动的时间与速度偏向角正切值之间函数关系如图所示,g取10m/s2,则下列说法中正确的是( )
平抛运动任意时刻速度的方向与水平方向的夹角定义为速度的偏向角,某物体做平抛运动的时间与速度偏向角正切值之间函数关系如图所示,g取10m/s2,则下列说法中正确的是( )| A. | 1s末物体的速度大小为$5\sqrt{5}$m/s | |
| B. | 平抛的初速度大小为20m/s | |
| C. | 第1s内物体的位移大小为$\sqrt{5}$m | |
| D. | 第1s内物体位移的方向与水平方向夹角的正切值为1 |
7.物体的加速度大小为3m/s2,表示此物体( )
| A. | 每秒运动3m | |
| B. | 每经过1s,其速度增大3m/s | |
| C. | 每经过1s,其速度增量的大小为3m/s | |
| D. | 每经过1s,其速度减小3m/s |
8.下列关于物体重心的说法中,正确的是( )
| A. | 物体的重心必在物体上 | |
| B. | 形状规则的物体的重心就在物体的几何中心 | |
| C. | 重心是物体各部分所受重力的合力的等效作用点 | |
| D. | 重心就是物体内最重的一点 |
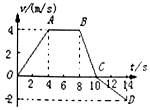 如图表示某物体做直线运动的v-t图象,从图可知:
如图表示某物体做直线运动的v-t图象,从图可知: 如图所示,一个质量为10kg的物体挂在弹簧上,弹簧伸长了0.2m,再将弹簧拉长0.1m,然后放开,求弹簧的运动规律(设阻尼系数为0).
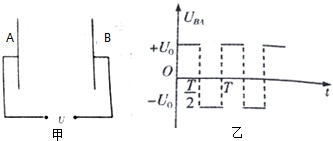
如图所示,一个质量为10kg的物体挂在弹簧上,弹簧伸长了0.2m,再将弹簧拉长0.1m,然后放开,求弹簧的运动规律(设阻尼系数为0). 某同学用如图甲所示的器材和电路测量电源电动势和内电阻.
某同学用如图甲所示的器材和电路测量电源电动势和内电阻.