题目内容
7. 如图所示,在空中的M点分别以不同的速率将两小球a、b水平抛出,分别落在水平地面上的P点和Q点.已知O点时M点在地面上的竖直投影,不考虑空气阻力的影响.下列说法中正确的是( )
如图所示,在空中的M点分别以不同的速率将两小球a、b水平抛出,分别落在水平地面上的P点和Q点.已知O点时M点在地面上的竖直投影,不考虑空气阻力的影响.下列说法中正确的是( )| A. | a小球先落地 | |
| B. | b小球落地时的速度较大 | |
| C. | a小球落地时速度与竖直方向的夹角较大 | |
| D. | b小球落地时速度与竖直方向的夹角较大 |
分析 根据高度比较平抛运动的时间,抓住水平位移和时间比较初速度,从而结合平行四边形定则判断落地的速度大小以及落地速度方向与竖直方向的夹角.
解答 解:A、a、b两球下降的高度相等,则平抛运动的时间相等,两球同时落地,故A错误.
B、b球的水平位移大,时间相同,则b球的初速度大,根据平行四边形定则知,v=$\sqrt{{{v}_{0}}^{2}+{{v}_{y}}^{2}}=\sqrt{{{v}_{0}}^{2}+2gh}$,可知b球落地时的速度较大,故B正确.
C、设小球落地速度方向与竖直方向的夹角为θ,根据平行四边形定则知,$tanθ=\frac{{v}_{0}}{{v}_{y}}$,落地时的竖直分速度相等,b球初速度大,则b小球落地时速度与竖直方向的夹角较大,故C错误,D正确.
故选:BD.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,知道运动的时间由高度决定,与初速度无关,初速度和时间共同决定水平位移.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
17.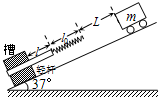 倾角为37°的光滑斜面上固定一个槽,劲度系数k=20N/m,原长l0=0.6m的轻弹簧下端与轻杆相连,开始时杆在槽外的长度l=0.3m,且杆可在槽内移动,杆与槽间的滑动摩擦力大小F1=6N,杆与槽之间的最大静摩擦力等于滑动摩擦力,质量m=1kg的小车从距弹簧上端L=0.6m处由静止释放沿斜面向下运动.已知弹性势能Ep=$\frac{1}{2}$kx2,式中x为弹簧的形变量,g=10m/s2,sin37°=0.6,关于小车和杆的运动情况,下列说法正确的是( )
倾角为37°的光滑斜面上固定一个槽,劲度系数k=20N/m,原长l0=0.6m的轻弹簧下端与轻杆相连,开始时杆在槽外的长度l=0.3m,且杆可在槽内移动,杆与槽间的滑动摩擦力大小F1=6N,杆与槽之间的最大静摩擦力等于滑动摩擦力,质量m=1kg的小车从距弹簧上端L=0.6m处由静止释放沿斜面向下运动.已知弹性势能Ep=$\frac{1}{2}$kx2,式中x为弹簧的形变量,g=10m/s2,sin37°=0.6,关于小车和杆的运动情况,下列说法正确的是( )
 倾角为37°的光滑斜面上固定一个槽,劲度系数k=20N/m,原长l0=0.6m的轻弹簧下端与轻杆相连,开始时杆在槽外的长度l=0.3m,且杆可在槽内移动,杆与槽间的滑动摩擦力大小F1=6N,杆与槽之间的最大静摩擦力等于滑动摩擦力,质量m=1kg的小车从距弹簧上端L=0.6m处由静止释放沿斜面向下运动.已知弹性势能Ep=$\frac{1}{2}$kx2,式中x为弹簧的形变量,g=10m/s2,sin37°=0.6,关于小车和杆的运动情况,下列说法正确的是( )
倾角为37°的光滑斜面上固定一个槽,劲度系数k=20N/m,原长l0=0.6m的轻弹簧下端与轻杆相连,开始时杆在槽外的长度l=0.3m,且杆可在槽内移动,杆与槽间的滑动摩擦力大小F1=6N,杆与槽之间的最大静摩擦力等于滑动摩擦力,质量m=1kg的小车从距弹簧上端L=0.6m处由静止释放沿斜面向下运动.已知弹性势能Ep=$\frac{1}{2}$kx2,式中x为弹簧的形变量,g=10m/s2,sin37°=0.6,关于小车和杆的运动情况,下列说法正确的是( )| A. | 小车先做匀加速运动,然后做加速度逐渐减小的变加速运动,最后做匀速直线运动 | |
| B. | 小车先做匀加速运动,后做加速度逐渐减小的变加速运动 | |
| C. | 杆刚要滑动时小车已通过的位移为0.9m | |
| D. | 杆从开始运动到完全进入槽内所用时间为0.1s |
15. 边长为L的正方形金属框以初速度v0穿过方向如图所示的有界匀强磁场,磁场宽度为d(d>L),金属框从进入磁场到完全穿出磁场整个过程只受安培力作用,则金属框进入磁场过程和从磁场另外一侧穿出过程相比较,说法正确的( )
边长为L的正方形金属框以初速度v0穿过方向如图所示的有界匀强磁场,磁场宽度为d(d>L),金属框从进入磁场到完全穿出磁场整个过程只受安培力作用,则金属框进入磁场过程和从磁场另外一侧穿出过程相比较,说法正确的( )
 边长为L的正方形金属框以初速度v0穿过方向如图所示的有界匀强磁场,磁场宽度为d(d>L),金属框从进入磁场到完全穿出磁场整个过程只受安培力作用,则金属框进入磁场过程和从磁场另外一侧穿出过程相比较,说法正确的( )
边长为L的正方形金属框以初速度v0穿过方向如图所示的有界匀强磁场,磁场宽度为d(d>L),金属框从进入磁场到完全穿出磁场整个过程只受安培力作用,则金属框进入磁场过程和从磁场另外一侧穿出过程相比较,说法正确的( )| A. | 两过程中a点的电势均高于 b点电势 | |
| B. | 两过程中速度变化量相同 | |
| C. | 两过程中产生的热量相同 | |
| D. | 两过程所用的时间相同 |
12.下列对理想气体的理解正确的是( )
| A. | 理想气体的压强是由气体分子间斥力产生的 | |
| B. | 只要气体压强不是很大就可视为理想气体 | |
| C. | 容积不变的密闭容器内的理想气体随着温度的升高,其压强增大,内能增大 | |
| D. | 一定质量的理想气体对外界做功时,它的内能有可能增大 | |
| E. | 理想气体实际上并不存在,只是一种理想模型 |
19.下列有关原子结构和原子核的认识,其中正确的是( )
| A. | β粒子带负电,所以β射线有可能是核外电子 | |
| B. | 氢原子辐射光子后,其绕核运动的电子动能减小,电势能增大 | |
| C. | 太阳辐射能量的主要来源是太阳中发生的轻核聚变 | |
| D. | 居里夫妇发现了铀和含铀矿物的天然放射现象 |
14. 如图所示,在水平面上有两条导电导轨MN、PQ,导轨间距为d,足够大区域的匀强磁场垂直于导轨所在的平面向里,磁感应强度的大小为B,两根完全相同的金属杆1、2间隔一定的距离摆开放在导轨上,且与导轨垂直.它们的电阻均为R,两杆与导轨接触良好,导轨电阻不计,金属杆的摩擦不计.杆2不固定,杆1以初速度v0滑向杆2,为使两杆不相碰,最初摆放两杆时的距离可以为( )
如图所示,在水平面上有两条导电导轨MN、PQ,导轨间距为d,足够大区域的匀强磁场垂直于导轨所在的平面向里,磁感应强度的大小为B,两根完全相同的金属杆1、2间隔一定的距离摆开放在导轨上,且与导轨垂直.它们的电阻均为R,两杆与导轨接触良好,导轨电阻不计,金属杆的摩擦不计.杆2不固定,杆1以初速度v0滑向杆2,为使两杆不相碰,最初摆放两杆时的距离可以为( )
 如图所示,在水平面上有两条导电导轨MN、PQ,导轨间距为d,足够大区域的匀强磁场垂直于导轨所在的平面向里,磁感应强度的大小为B,两根完全相同的金属杆1、2间隔一定的距离摆开放在导轨上,且与导轨垂直.它们的电阻均为R,两杆与导轨接触良好,导轨电阻不计,金属杆的摩擦不计.杆2不固定,杆1以初速度v0滑向杆2,为使两杆不相碰,最初摆放两杆时的距离可以为( )
如图所示,在水平面上有两条导电导轨MN、PQ,导轨间距为d,足够大区域的匀强磁场垂直于导轨所在的平面向里,磁感应强度的大小为B,两根完全相同的金属杆1、2间隔一定的距离摆开放在导轨上,且与导轨垂直.它们的电阻均为R,两杆与导轨接触良好,导轨电阻不计,金属杆的摩擦不计.杆2不固定,杆1以初速度v0滑向杆2,为使两杆不相碰,最初摆放两杆时的距离可以为( )| A. | $\frac{mR{v}_{0}}{{B}^{2}{d}^{2}}$ | B. | $\frac{mR{v}_{0}}{2{B}^{2}{d}^{2}}$ | C. | $\frac{2mR{v}_{0}}{{B}^{2}{d}^{2}}$ | D. | $\frac{mR{v}_{0}}{4{B}^{2}{d}^{2}}$ |
 2016年10月22 日是世界传统医药日,按摩拔火罐等中医疗法成办公室年轻人新宠.如图所示,若罐的容积为45cm3,罐内空气温度为27℃.已知大气压P0=1×105Pa,求:
2016年10月22 日是世界传统医药日,按摩拔火罐等中医疗法成办公室年轻人新宠.如图所示,若罐的容积为45cm3,罐内空气温度为27℃.已知大气压P0=1×105Pa,求: 一辆由电动机提供牵引力的实验小车在水平的直轨道上由静止开始运动,其运动的全过程转化为如图所示的v-t图象,图象显示2s-10s时间段内的图象为曲线,其余时间段图象均为直线.已知实验小车运动的过程中,2s-14s时间段内小车的功率保持不变,在14s末关闭发动机而让小车自由滑行.已知小车的质量为1kg,假设在整个运动过程中小车所受到的阻力大小不变.求:
一辆由电动机提供牵引力的实验小车在水平的直轨道上由静止开始运动,其运动的全过程转化为如图所示的v-t图象,图象显示2s-10s时间段内的图象为曲线,其余时间段图象均为直线.已知实验小车运动的过程中,2s-14s时间段内小车的功率保持不变,在14s末关闭发动机而让小车自由滑行.已知小车的质量为1kg,假设在整个运动过程中小车所受到的阻力大小不变.求: