题目内容
6.如图甲所示,在圆形水池正上方,有一半径为r的圆形储水桶.水桶底部有多个沿半径方向的水平小孔,小孔喷出的水在水池中的落点离水池中心的距离为R,水桶底部与水池水面之间的高度差是h.为了维持水桶水面的高度不变,用水泵通过细水管将洒落的水重新抽回到高度差为H的水桶上方.水泵由效率为η1的太阳能电池板供电,电池板与水平面之间的夹角为α,太阳光竖直向下照射(如图乙所示),太阳光垂直照射时单位时间、单位面积接受的能量为E0.水泵的效率为η2,水泵出水口单位时间流出水的质量为m0,流出水流的速度大小为v0(不计水在细水管和空气中运动时所受的阻力).求:
(1)水从小孔喷出时的速度大小;
(2)水泵的输出功率;
(3)为了使水泵的工作能维持水面的高度不变,太阳能电池板面积的最小值S.
分析 (1)由题意可知水做平抛运动的水平位移及竖直高度,则由平抛运动规律可得出水从小孔中喷出的速度;
(2)由功能关系可求得水泵做的功,由功率公式可求得功率;
(3)由太阳能及水泵在转化中的效率可求得实际需要的太阳能量,则可求得太阳能的电池板面积的最小值.
解答 解:(1)水从小孔喷出时速度沿水平方向,只受重力作用,做平抛运动,设水喷出时的速度大小为v,有:
R-r=vt
h=$\frac{1}{2}$gt2;
水喷出的速度为:v=$\frac{(R-r)\sqrt{2gh}}{2h}$;
(2)水泵做功,既改变水的势能,又改变水的动能.由功能关系得:
Pt=m0tgh+$\frac{1}{2}$m0tv02;
功率为:P=m0gh+$\frac{1}{2}$m0v02.
(3)考虑单位时间内的能量转化及利用效率,太阳能电池板接收太阳能的其中一部分转变成电能E1,电能通过水泵将其中的部分转变成水的势能与动能E2,有:
E1=η1E0cosθ
E2=η2E1
E2=m0gH+$\frac{1}{2}$m0v02
解得最小面积为:S=$\frac{{m}_{0}gH+\frac{1}{2}{{m}_{0}v}_{0}^{2}}{{η}_{1}{η}_{2}{E}_{0}cosα}$;
答:(1)水从小孔喷出时的速度大小为$\frac{(R-r)\sqrt{2gh}}{2h}$;
(2)水泵的输出功率为m0gh+$\frac{1}{2}$m0v02.;
(3)为了使水泵的工作能维持水面的高度不变,太阳能电池板面积的最小值S$\frac{{m}_{0}gH+\frac{1}{2}{{m}_{0}v}_{0}^{2}}{{η}_{1}{η}_{2}{E}_{0}cosα}$.
点评 本题根据生活中的例子考查功能的关系,解题的关键在于明确题意,从而构建出我们所熟知的物理模型,则可轻松解决本题.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案 人站在岸上通过定滑轮用绳牵引低处的小船,如图所示,若水的阻力恒定不变,则在船匀速靠岸的过程中,下列说法正确的是( )
人站在岸上通过定滑轮用绳牵引低处的小船,如图所示,若水的阻力恒定不变,则在船匀速靠岸的过程中,下列说法正确的是( )| A. | 人收绳的速度越来越大 | B. | 人收绳的速度越来越慢 | ||
| C. | 船受到的浮力保持减小 | D. | 船受到的浮力不断不变 |

| A. | 两电阻串联后的伏安曲线在区域I内,两电阻并联后的伏安曲线在区域II内 | |
| B. | 两电阻串联后的伏安曲线在区域III内,两电阻并联后的伏安曲线在区域I内 | |
| C. | A、B电阻阻值之比为 1:3 | |
| D. | A、B电阻阻值之比为 3:1 |
| A. | $\frac{1}{2}$mv12 | B. | mg(H+h) | C. | $\frac{1}{2}$mv12+mgh | D. | $\frac{1}{2}$mv22-mgh |
| A. | 减少路轨阻力,有利于提高列车最高时速 | |
| B. | 当列车保持最高时速行驶时,其牵引力与阻力大小相等 | |
| C. | 列车的最高时速取决于其最大功率、阻力及相关技术 | |
| D. | 将列车车头做成流线形,减小空气阻力,有利于提高列车功率 |

| A. | 向右减速运动 | B. | 向右加速运动 | C. | 向左减速运动 | D. | 向左匀速运动 |
 如图所示,在光滑水平直导轨上,静止放着三个质量均为m=1kg的相同小球A、B、C.现让A球以v0=2m/s的速度向着B球运动,A、B两球碰撞后粘在一起,两球继续向右运动并跟C球碰撞,C球的最终速度vC=1m/s.则:
如图所示,在光滑水平直导轨上,静止放着三个质量均为m=1kg的相同小球A、B、C.现让A球以v0=2m/s的速度向着B球运动,A、B两球碰撞后粘在一起,两球继续向右运动并跟C球碰撞,C球的最终速度vC=1m/s.则: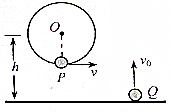 如图所示,小球P固定于圆盘上,小球Q位于地面上,开始时小球P从圆盘的最低点绕圆盘的圆心做匀速圆周运动,同时小球Q以初速度v0=8m/s做竖直上抛运动,已知圆盘的圆心离地面的高h=2.4m,g=10m/s2,在运动过程中发现两小球在同一高度有速度相等的情况存在,问圆盘的半径是多大?
如图所示,小球P固定于圆盘上,小球Q位于地面上,开始时小球P从圆盘的最低点绕圆盘的圆心做匀速圆周运动,同时小球Q以初速度v0=8m/s做竖直上抛运动,已知圆盘的圆心离地面的高h=2.4m,g=10m/s2,在运动过程中发现两小球在同一高度有速度相等的情况存在,问圆盘的半径是多大?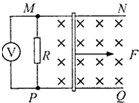 如图所示,光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上,两导轨间距l=0.2m,电阻R=0.4Ω,导轨上静止放置一质量m=0.1kg、电阻r=0.1Ω的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度B=0.5T的匀强磁场中,磁场的方向竖直向下,现用一外力F沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,杆以加速度a=2m/s2匀加速运动5秒
如图所示,光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上,两导轨间距l=0.2m,电阻R=0.4Ω,导轨上静止放置一质量m=0.1kg、电阻r=0.1Ω的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度B=0.5T的匀强磁场中,磁场的方向竖直向下,现用一外力F沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,杆以加速度a=2m/s2匀加速运动5秒