题目内容
15. 辊式破裂机的原理如图所示.两圆柱型轧辊转动时能把矿石轧入轧辊间隙,并使之破碎,已知轧辊的直径为D,轧辊间隙为l,矿石与轧辊之间的静摩擦因数为μ,把矿石看成球体,则能轧入且被破碎的矿石的最大直径d是(矿石的重量不计)(D+l)$\sqrt{1+{μ}^{2}}$-D.
辊式破裂机的原理如图所示.两圆柱型轧辊转动时能把矿石轧入轧辊间隙,并使之破碎,已知轧辊的直径为D,轧辊间隙为l,矿石与轧辊之间的静摩擦因数为μ,把矿石看成球体,则能轧入且被破碎的矿石的最大直径d是(矿石的重量不计)(D+l)$\sqrt{1+{μ}^{2}}$-D.
分析 料石重力不计,故要使矿石进入轧棍只需要合力向下即可,则可知应保证摩擦力向下的分力大于等于支持力向上的分力,再分析题目中给出的几何关系即可找到夹角大小,再根据竖直方向的受力情况列式,联立即可求出最大直径d.
解答  解:设矿石直径为d,则由几何关系可知,轧棍与矿石圆心间的距离为$\frac{D+d}{2}$;
解:设矿石直径为d,则由几何关系可知,轧棍与矿石圆心间的距离为$\frac{D+d}{2}$;
图中x1=$\frac{D}{2}$+$\frac{l}{2}$;
x2=$\sqrt{(\frac{D+d}{2})^{2}-(\frac{D-l}{2})^{2}}$
则有:tanα=$\frac{{x}_{1}}{{x}_{2}}$=($\frac{\frac{D+l}{2}}{\sqrt{(\frac{D+d}{2})^{2}-(\frac{D-l}{2})^{2}}}$
要使矿石能进入轧棍,则应满足fcosα≥FNcosα
f=μFN
则有:μ≥tanα
则可解得:d≤(D+l)$\sqrt{1+{μ}^{2}}$-D
故最大直径为:(D+l)$\sqrt{1+{μ}^{2}}$-D
故答案为:(D+l)$\sqrt{1+{μ}^{2}}$-D
点评 本题考查“自锁”现象的应用,要注意明确只要矿石小于一个定值,则摩擦力一定可以保证矿石向下运动进入轧棍,不论质量大小,本题属于竞赛类考查的内容,难度较大,要注意认真体会其中的几何关系,注意本题中为了便于分析几何关系,没有画出摩擦力和支持力的分力,在自已分析时应注意体会它们在竖直方向上的分力与摩擦角α之间的关系.

练习册系列答案
相关题目
4. 如图所示,一平行板电容器,带电量为Q,上极板带正电,下极板带负电,在两板中间放入一不带电的导体(宽度小于板间距),在板中间有三点1、2、3,对应的场强分别是E1、E2、E3把导体移走后三点的场强分别是E1'E2'E3',则下列说法正确的是( )
如图所示,一平行板电容器,带电量为Q,上极板带正电,下极板带负电,在两板中间放入一不带电的导体(宽度小于板间距),在板中间有三点1、2、3,对应的场强分别是E1、E2、E3把导体移走后三点的场强分别是E1'E2'E3',则下列说法正确的是( )
 如图所示,一平行板电容器,带电量为Q,上极板带正电,下极板带负电,在两板中间放入一不带电的导体(宽度小于板间距),在板中间有三点1、2、3,对应的场强分别是E1、E2、E3把导体移走后三点的场强分别是E1'E2'E3',则下列说法正确的是( )
如图所示,一平行板电容器,带电量为Q,上极板带正电,下极板带负电,在两板中间放入一不带电的导体(宽度小于板间距),在板中间有三点1、2、3,对应的场强分别是E1、E2、E3把导体移走后三点的场强分别是E1'E2'E3',则下列说法正确的是( )| A. | 导体的上表面a带负电,下表面b带正电 | |
| B. | E1>E2>E3 | |
| C. | E1'=E2'=E3' | |
| D. | E1'>E3>E2 |
 如图所示,小球从竖直砖墙某位置静止释放作自由落体运动,用频闪照相机在同一底片上多次曝光,得到了图中1、2、3、4、5…所示小球运动过程中每次曝光的位置.连续两次曝光的时间间隔相等,每块砖的厚度为10cm.根据图中的信息,可知两次连续曝光的时间间隔为0.1s,小球在位置“3”的速度为3.5m/s.(g=10m/s2)
如图所示,小球从竖直砖墙某位置静止释放作自由落体运动,用频闪照相机在同一底片上多次曝光,得到了图中1、2、3、4、5…所示小球运动过程中每次曝光的位置.连续两次曝光的时间间隔相等,每块砖的厚度为10cm.根据图中的信息,可知两次连续曝光的时间间隔为0.1s,小球在位置“3”的速度为3.5m/s.(g=10m/s2) 如图所示,用两根轻质绳把重为Mg的不均匀棒悬挂起来呈水平静止状态,一棍绳子同竖直方向夹角θ1=37°,另一根同竖直方向夹角θ2=53°.棒长L=6.0m,问重心离右端的距离x等于多少?
如图所示,用两根轻质绳把重为Mg的不均匀棒悬挂起来呈水平静止状态,一棍绳子同竖直方向夹角θ1=37°,另一根同竖直方向夹角θ2=53°.棒长L=6.0m,问重心离右端的距离x等于多少?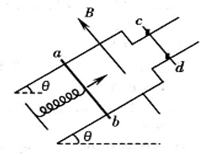 如图所示,固定的光滑金属导轨电阻不计,导轨平面与水平面的夹角为θ,整个装置处在磁感应强度大小为B、方向垂直于导轨平面向上的匀强磁场中,导轨较宽部分宽度为L1,较窄部分宽度为L2,质量为m1的导体棒ab与固定弹簧相连后放在较宽导轨上,较窄导轨上固定两立柱,其上放置一质量为m2导体棒cd,导体棒ab、cd接入电路的电阻分别为R、r.初始时刻,弹簧恰处于自然长度,导体棒ab具有沿轨道向上的初速度,此时两立柱对导体棒cd的支持力恰好为零.整个运动过程中,导体棒ab始终与导轨垂直并保持良好接触,导体棒cd始终静止不动.已知弹簧的劲度系数为k,弹簧的中心轴线与导轨平行,重力加速度为g.求:
如图所示,固定的光滑金属导轨电阻不计,导轨平面与水平面的夹角为θ,整个装置处在磁感应强度大小为B、方向垂直于导轨平面向上的匀强磁场中,导轨较宽部分宽度为L1,较窄部分宽度为L2,质量为m1的导体棒ab与固定弹簧相连后放在较宽导轨上,较窄导轨上固定两立柱,其上放置一质量为m2导体棒cd,导体棒ab、cd接入电路的电阻分别为R、r.初始时刻,弹簧恰处于自然长度,导体棒ab具有沿轨道向上的初速度,此时两立柱对导体棒cd的支持力恰好为零.整个运动过程中,导体棒ab始终与导轨垂直并保持良好接触,导体棒cd始终静止不动.已知弹簧的劲度系数为k,弹簧的中心轴线与导轨平行,重力加速度为g.求: 如图所示,宽为1m平行光滑导轨水平放置,在导轨间有磁感应强度1T的匀强磁场,长为2m、电阻为2Ω的金属棒PQ以1m/s速度贴着导轨向右运动,R=3Ω,其它部分电阻不计.
如图所示,宽为1m平行光滑导轨水平放置,在导轨间有磁感应强度1T的匀强磁场,长为2m、电阻为2Ω的金属棒PQ以1m/s速度贴着导轨向右运动,R=3Ω,其它部分电阻不计.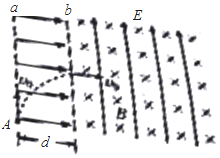 如图所示,竖直平面内竖直方向的直线a、b宽度为d,直线a、b之间有方向水平向右电场强度为E的匀强电场,直线b的右侧有竖直向上电场强度大小仍为E的匀强电场和垂直纸面向里的匀强磁场.令有质量为m的带正电微粒从直线a上的A点以某一速度竖直向上运动,当它到达直线b上时,速度变为水平方向,且大小与A点的速度大小相同,竖直方向的位移为d,然后进入直线b右侧的电磁场区域运动,又从距离A竖直高度为2d的位置再次进入直线a、b之间运动,重力加速度为g,直线b右侧的电磁场区域非常宽.求:
如图所示,竖直平面内竖直方向的直线a、b宽度为d,直线a、b之间有方向水平向右电场强度为E的匀强电场,直线b的右侧有竖直向上电场强度大小仍为E的匀强电场和垂直纸面向里的匀强磁场.令有质量为m的带正电微粒从直线a上的A点以某一速度竖直向上运动,当它到达直线b上时,速度变为水平方向,且大小与A点的速度大小相同,竖直方向的位移为d,然后进入直线b右侧的电磁场区域运动,又从距离A竖直高度为2d的位置再次进入直线a、b之间运动,重力加速度为g,直线b右侧的电磁场区域非常宽.求: