题目内容
6. 如图所示,用两根轻质绳把重为Mg的不均匀棒悬挂起来呈水平静止状态,一棍绳子同竖直方向夹角θ1=37°,另一根同竖直方向夹角θ2=53°.棒长L=6.0m,问重心离右端的距离x等于多少?
如图所示,用两根轻质绳把重为Mg的不均匀棒悬挂起来呈水平静止状态,一棍绳子同竖直方向夹角θ1=37°,另一根同竖直方向夹角θ2=53°.棒长L=6.0m,问重心离右端的距离x等于多少?
分析 做出棒的受力分析图,利用物体受到的共点力平衡,确定物体受到的三个力的作用线交与一点,然后写出力的平衡方程即可.
解答 解:设棒的两端分别为AB,如图对棒进行受力分析:
因:θ1+θ2=90°
所以:FA和FB垂直,重力的作用线与棒的交点就是棒的重心所在的位置,
设该点为O′,设三条作用线的交点为O,由几何关系得:$x=\overline{AB}•cos{θ}_{1}•cos{θ}_{1}=6×\frac{4}{5}×\frac{4}{5}$=3.84m
答:重心离右端的距离x等于3.84m.
点评 该题中利用物体受到的共点力平衡,确定物体受到的三个力的作用线交与一点,从而确定棒的重心的位置是解题的关键.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
15. 2013年12月14日嫦娥三号探测器成功软着陆于月球雨海西北部,假设嫦娥三号先沿距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点时,点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B时再次点火进入月球近月轨道Ⅲ绕月球做圆周运动,如图所示,已知月球半径为R,月球表面的重力加速度为g,则嫦娥三号( )
2013年12月14日嫦娥三号探测器成功软着陆于月球雨海西北部,假设嫦娥三号先沿距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点时,点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B时再次点火进入月球近月轨道Ⅲ绕月球做圆周运动,如图所示,已知月球半径为R,月球表面的重力加速度为g,则嫦娥三号( )
 2013年12月14日嫦娥三号探测器成功软着陆于月球雨海西北部,假设嫦娥三号先沿距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点时,点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B时再次点火进入月球近月轨道Ⅲ绕月球做圆周运动,如图所示,已知月球半径为R,月球表面的重力加速度为g,则嫦娥三号( )
2013年12月14日嫦娥三号探测器成功软着陆于月球雨海西北部,假设嫦娥三号先沿距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点时,点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B时再次点火进入月球近月轨道Ⅲ绕月球做圆周运动,如图所示,已知月球半径为R,月球表面的重力加速度为g,则嫦娥三号( )| A. | 在轨道Ⅰ上运行的角速度为ω=$\sqrt{\frac{g}{64R}}$ | |
| B. | 在轨道Ⅱ上运行的周期大于在轨道Ⅰ上运动的周期 | |
| C. | 在轨道Ⅱ上经过A点时的加速度小于在轨道Ⅰ上经过A点时的加速度 | |
| D. | 在轨道Ⅰ上经过A点时的速度小于在轨道Ⅲ经过B点的速度 |
16.下列情况中的物体,哪个可以看作质点( )
| A. | 研究地球自转时的地球 | |
| B. | 研究汽车后轮上一点运动情况的车轮 | |
| C. | 体育教练员研究百米赛跑运动员的起跑动作 | |
| D. | 研究从北京开往上海的一列火车的运行速度 |
1.图甲是在高速公路上用超声波测速仪测量车速的示意图,测速仪发出并接收超声波脉冲信号.根据发出和接收到的信号间的时间差,测出被测物体的速度.图乙中p1、p2是测速仪发出的超声波信号,n1、n2分别是p1、p2由汽车反射回来的信号.设测速仪匀速扫描,p1、p2之间的时间间隔△t=1.0s,超声波在空气中传播的速度是
v=340m/s,若汽车是匀速运动的,设汽车在接收到p1、p2两个信号之间的时间内前进的距离是△x,汽车的速度是v,则根据图可知( )
v=340m/s,若汽车是匀速运动的,设汽车在接收到p1、p2两个信号之间的时间内前进的距离是△x,汽车的速度是v,则根据图可知( )

| A. | △x=17m | B. | △x=34m | C. | 18.9m/s | D. | 17.9m/s |
16. 如图所示,直线A为电源a的路端电压与电流的关系图象,直线B为电源b的路端电压与电流的关系图象,直线C为一个电阻R的两端电压与电流的关系图象.将这个电阻R分别接到a,b两电源上,那么( )
如图所示,直线A为电源a的路端电压与电流的关系图象,直线B为电源b的路端电压与电流的关系图象,直线C为一个电阻R的两端电压与电流的关系图象.将这个电阻R分别接到a,b两电源上,那么( )
 如图所示,直线A为电源a的路端电压与电流的关系图象,直线B为电源b的路端电压与电流的关系图象,直线C为一个电阻R的两端电压与电流的关系图象.将这个电阻R分别接到a,b两电源上,那么( )
如图所示,直线A为电源a的路端电压与电流的关系图象,直线B为电源b的路端电压与电流的关系图象,直线C为一个电阻R的两端电压与电流的关系图象.将这个电阻R分别接到a,b两电源上,那么( )| A. | R接到a电源上,电源a有最大输出功率 | |
| B. | R接到b电源上,电源b有最大输出功率 | |
| C. | R接到a电源上,电源的输出功率较大,但电源效率较低 | |
| D. | R接到b电源上,电阻的发热功率和电源的效率都较高 |
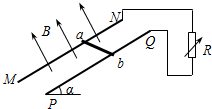 如图所示,光滑且足够长平行金属导轨MN.PQ相距L=1m,导轨平面与水平面夹角α=30°,导轨电阻不计.磁感应强度B=2T的匀强磁场垂直导轨平面斜向上,一金属棒ab垂直于MN.PQ放置在导轨上,且始终与导轨接触良好,金属棒质量m=0.8kg,电阻r=2Ω.两金属导轨的上端连接一电阻箱R,调节电阻箱使R=8Ω,现
如图所示,光滑且足够长平行金属导轨MN.PQ相距L=1m,导轨平面与水平面夹角α=30°,导轨电阻不计.磁感应强度B=2T的匀强磁场垂直导轨平面斜向上,一金属棒ab垂直于MN.PQ放置在导轨上,且始终与导轨接触良好,金属棒质量m=0.8kg,电阻r=2Ω.两金属导轨的上端连接一电阻箱R,调节电阻箱使R=8Ω,现 如图所示,有一宽L=0.4m的矩形金属框架水平放置,右端接一个阻值R=2Ω的电阻,框架的其他部分电阻不计,框架足够长.垂直金属框平面有一竖直向下的匀强磁场,磁感应强度B=1T.金属杆ab质量m=0.1kg,电阻r=1Ω,杆与框架接触良好,且与框架间的摩擦力不计.当杆受一水平恒定拉力F作用时刚好可以在框架上做匀速运动,速度大小为v=3m/s.求:
如图所示,有一宽L=0.4m的矩形金属框架水平放置,右端接一个阻值R=2Ω的电阻,框架的其他部分电阻不计,框架足够长.垂直金属框平面有一竖直向下的匀强磁场,磁感应强度B=1T.金属杆ab质量m=0.1kg,电阻r=1Ω,杆与框架接触良好,且与框架间的摩擦力不计.当杆受一水平恒定拉力F作用时刚好可以在框架上做匀速运动,速度大小为v=3m/s.求: 辊式破裂机的原理如图所示.两圆柱型轧辊转动时能把矿石轧入轧辊间隙,并使之破碎,已知轧辊的直径为D,轧辊间隙为l,矿石与轧辊之间的静摩擦因数为μ,把矿石看成球体,则能轧入且被破碎的矿石的最大直径d是(矿石的重量不计)(D+l)$\sqrt{1+{μ}^{2}}$-D.
辊式破裂机的原理如图所示.两圆柱型轧辊转动时能把矿石轧入轧辊间隙,并使之破碎,已知轧辊的直径为D,轧辊间隙为l,矿石与轧辊之间的静摩擦因数为μ,把矿石看成球体,则能轧入且被破碎的矿石的最大直径d是(矿石的重量不计)(D+l)$\sqrt{1+{μ}^{2}}$-D.