题目内容
14.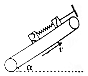 如图所示,倾角为α的传送带上有质量均为m的两个木块1、2,它们之间用原长为L、劲度系数为k的轻弹簧连接起来,木块与传送带间的动摩擦因数均为μ,其中木块1被与传送带平行的细线拉住,传动带按图示方向匀速运动,两个木块均处于平衡状态.求:
如图所示,倾角为α的传送带上有质量均为m的两个木块1、2,它们之间用原长为L、劲度系数为k的轻弹簧连接起来,木块与传送带间的动摩擦因数均为μ,其中木块1被与传送带平行的细线拉住,传动带按图示方向匀速运动,两个木块均处于平衡状态.求:(1)1、2两木块之间的距离.
(2)细线断开的一瞬间,木块1与木块2的加速度大小.
分析 (1)对木块2分析,根据共点力平衡求出弹簧的弹力,结合胡克定律求出弹簧的形变量,从而求出1、2两木块之间的距离.
(2)细线断开的一瞬间,弹簧的弹力和滑动摩擦力均不变.根据牛顿第二定律求两者的加速度.
解答 解:(1)对木块2进行受力分析,如图所示,设弹簧的伸长量为△x,因为木块处于平衡状态,
故有:k•△x=mgsinα+μmgcosα,
则1、2两木块之间的距离 S=L+△x
联立解得 S=L+$\frac{mg(sinα+μcosα)}{k}$
(2)细线断开的一瞬间,弹簧的弹力和滑动摩擦力均不变,则木块2的受力情况不变,加速度为0.
对木块1,由牛顿第二定律得:mgsinα+μmgcosα+k•△x=ma
解得:a=2g(sinα+μcosα)
答:
(1)1、2两木块之间的距离是L+$\frac{mg(sinα+μcosα)}{k}$.
(2)细线断开的一瞬间,木块1与木块2的加速度大小分别为2g(sinα+μcosα)和0.
点评 解决本题的关键能够正确地受力分析,运用共点力平衡进行求解,掌握整体法和隔离法的运用.分析受力情况时,要注意分析滑动摩擦力的方向,要抓住滑动摩擦力方向与物体相对运动方向相反.

练习册系列答案
相关题目
5.哪位科学家终于在1831年发现了电磁感应现象,进一步揭示了电现象与磁现象之间的密切联系,奏响了电气化时代的序曲( )
| A. | 法拉第 | B. | 奥斯特 | C. | 爱迪生 | D. | 斯旺 |
2. 如图所示为一绕地球运行的人造地球卫星运行轨迹,卫星近地点P近似认为贴近地球表面,远地点Q距地面的高度为h,已知地球半径为R,地球表面重力加速度为g,则( )
如图所示为一绕地球运行的人造地球卫星运行轨迹,卫星近地点P近似认为贴近地球表面,远地点Q距地面的高度为h,已知地球半径为R,地球表面重力加速度为g,则( )
 如图所示为一绕地球运行的人造地球卫星运行轨迹,卫星近地点P近似认为贴近地球表面,远地点Q距地面的高度为h,已知地球半径为R,地球表面重力加速度为g,则( )
如图所示为一绕地球运行的人造地球卫星运行轨迹,卫星近地点P近似认为贴近地球表面,远地点Q距地面的高度为h,已知地球半径为R,地球表面重力加速度为g,则( )| A. | 该卫星的运动周期为2π$\sqrt{\frac{(R+\frac{h}{2})^{2}}{g{R}^{2}}}$ | |
| B. | 该卫星的发射速度大于第一宇宙速度 | |
| C. | 该卫星在P点的速度大小为$\sqrt{gR}$ | |
| D. | 该卫星在P点的加速度大于地球表面的重力加速度g |
6. “嫦娥三号”从距月面高度为100km的环月圆轨道Ⅰ上的P点实施变轨,进入近月点为15km的椭圆轨道Ⅱ,由近月点Q成功落月,如图所示.关于“嫦娥三号”,下列说法正确的是( )
“嫦娥三号”从距月面高度为100km的环月圆轨道Ⅰ上的P点实施变轨,进入近月点为15km的椭圆轨道Ⅱ,由近月点Q成功落月,如图所示.关于“嫦娥三号”,下列说法正确的是( )
 “嫦娥三号”从距月面高度为100km的环月圆轨道Ⅰ上的P点实施变轨,进入近月点为15km的椭圆轨道Ⅱ,由近月点Q成功落月,如图所示.关于“嫦娥三号”,下列说法正确的是( )
“嫦娥三号”从距月面高度为100km的环月圆轨道Ⅰ上的P点实施变轨,进入近月点为15km的椭圆轨道Ⅱ,由近月点Q成功落月,如图所示.关于“嫦娥三号”,下列说法正确的是( )| A. | 沿轨道Ⅰ运动至P时,需制动减速才能进入轨道Ⅱ | |
| B. | 沿轨道Ⅱ运行的周期大于沿轨道Ⅰ运行的周期 | |
| C. | 沿轨道Ⅱ运行时,在P点的加速度大于在Q点的加速度 | |
| D. | 在轨道Ⅱ上由P点运行到Q点的过程中,万有引力对其做正功,它的动能增加,重力势能减小,机械能不变 |
3. 如图所示,a、b是截面为等腰直角三角形的两个相同的楔形物体,分别在垂直于斜边的大小相等的恒力F1、F2作用下静止在相同的竖直墙面上.则( )
如图所示,a、b是截面为等腰直角三角形的两个相同的楔形物体,分别在垂直于斜边的大小相等的恒力F1、F2作用下静止在相同的竖直墙面上.则( )
 如图所示,a、b是截面为等腰直角三角形的两个相同的楔形物体,分别在垂直于斜边的大小相等的恒力F1、F2作用下静止在相同的竖直墙面上.则( )
如图所示,a、b是截面为等腰直角三角形的两个相同的楔形物体,分别在垂直于斜边的大小相等的恒力F1、F2作用下静止在相同的竖直墙面上.则( )| A. | a受到摩擦力可能为零 | B. | b受到摩擦力可能为零 | ||
| C. | 墙面对a的弹力大于墙面对b的弹力 | D. | 墙面对a的弹力小于墙面对b的弹力 |
4.关于质点,下列说法中正确的是( )
| A. | 只有体积很小的物体才能看作质点 | |
| B. | 在跳水比赛中,裁判可以把运动员看成质点 | |
| C. | 在太空中进行飞船对接的宇航员观察该飞船,可把飞船看作质点 | |
| D. | 从地球上的控制中心跟踪观察在太空中飞行的宇宙飞船,可把飞船看作质点 |

