题目内容
17. 按照我国月球探测活动计划,共分两步.第一步“绕月”工程,圆满完成任务后,再开展第二步“落月”工程.假设月球半径为R,月球表面的重力加速度为g0,飞船沿距月球中心距离为3R的圆形轨道Ⅰ运动,到达轨道的A点,点火变轨进入椭圆轨道Ⅱ,到达轨道Ⅱ的近月点B再次点火进入近月轨道Ⅲ(B点离月球表面的高度小于月球的半径)绕月球做圆周运动,根据以上信息,求(1)飞船在轨道I上运行的速度大小;
按照我国月球探测活动计划,共分两步.第一步“绕月”工程,圆满完成任务后,再开展第二步“落月”工程.假设月球半径为R,月球表面的重力加速度为g0,飞船沿距月球中心距离为3R的圆形轨道Ⅰ运动,到达轨道的A点,点火变轨进入椭圆轨道Ⅱ,到达轨道Ⅱ的近月点B再次点火进入近月轨道Ⅲ(B点离月球表面的高度小于月球的半径)绕月球做圆周运动,根据以上信息,求(1)飞船在轨道I上运行的速度大小;(2)飞船在椭圆轨道Ⅱ上A处的加速度大小;
(3)飞船在椭圆轨道Ⅱ上从A处运动到B处的最短时间.
分析 (1)根据万有引力提供向心力和在地面上万有引力等于重力列方程联立求解;
(2)根据牛顿第二定律求解加速度大小;
(3)求解卫星在轨道Ⅰ上运动的周期,根据开普勒第三定律求解卫星在Ⅱ轨道上运动的周期,由此求解飞船在椭圆轨道Ⅱ上从A处运动到B处的最短时间.
解答 解:(1)飞船在轨道Ⅰ上,万有引力提供向心力:$\frac{GMm}{(3R)^{2}}$=m$\frac{{v}^{2}}{3R}$,
在月球表面,万有引力等于重力得:$\frac{GMm}{{R}^{2}}=m{g}_{0}$,
解得:v=$\sqrt{\frac{R{g}_{0}}{3}}$;
(2)根据牛顿第二定律可得:$\frac{GMm}{{(3R)}^{2}}$=ma,
解得:a=$\frac{{g}_{0}}{3}$;
(3)卫星在轨道Ⅰ上运动的周期为T1=$\frac{2π•3R}{v}$=$6π\sqrt{\frac{3R}{{g}_{0}}}$;
卫星在Ⅱ轨道运动的半长轴为$\frac{3R+R}{2}$=2R,
根据开普勒第三定律可得:$\frac{(3R)^{3}}{{T}_{1}^{2}}$=$\frac{{(2R)}^{3}}{{T}_{2}^{2}}$,
解得卫星在Ⅱ轨道上运动的周期为T2=$4π\sqrt{\frac{2R}{{g}_{0}}}$,
所以飞船在椭圆轨道Ⅱ上从A处运动到B处的最短时间为t=$\frac{{T}_{2}}{2}$=$2π\sqrt{\frac{2R}{{g}_{0}}}$.
答:(1)飞船在轨道I上运行的速度大小为$\sqrt{\frac{R{g}_{0}}{3}}$;
(2)飞船在椭圆轨道Ⅱ上A处的加速度大小为$\frac{{g}_{0}}{3}$;
(3)飞船在椭圆轨道Ⅱ上从A处运动到B处的最短时间为$2π\sqrt{\frac{2R}{{g}_{0}}}$.
点评 本题主要是考查了万有引力定律及其应用;解答此类题目一般要把握两条线:一是在星球表面,忽略星球自转的情况下,万有引力近似等于重力;二是根据万有引力提供向心力列方程进行解答.

| A. | 速度 | B. | 动量 | C. | 机械能 | D. | 加速度 |
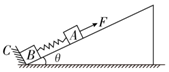 在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A沿斜面运动的距离为d,速度为v,则( )
在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A沿斜面运动的距离为d,速度为v,则( )| A. | 此过程中拉力F做功的大小等于物块A动能的增加量 | |
| B. | 当物块B刚要离开挡板时,受力满足m2gsinθ=kd | |
| C. | 当物块B刚要离开挡板时,物块A的加速度为$\frac{F-kd}{{m}_{1}}$ | |
| D. | 此过程中弹簧弹性势能的增加量为Fd-$\frac{1}{2}$m1v2-m1gdsinθ |
 如图所示,用两根足够长的粗糙金属条折成“『”型导轨,导轨左端竖直,右端水平,与导轨等宽的粗糙金属细杆ab、cd与导轨垂直且接触良好.已知ab、cd杆的质量、电阻值均相等,导轨电阻不计,整个装置处于竖直向上的匀强磁场中.当ab杆在水平拉力F作用下沿导轨向右匀速运动时,细杆cd杆沿轨道向下运动.以下说法正确的是( )
如图所示,用两根足够长的粗糙金属条折成“『”型导轨,导轨左端竖直,右端水平,与导轨等宽的粗糙金属细杆ab、cd与导轨垂直且接触良好.已知ab、cd杆的质量、电阻值均相等,导轨电阻不计,整个装置处于竖直向上的匀强磁场中.当ab杆在水平拉力F作用下沿导轨向右匀速运动时,细杆cd杆沿轨道向下运动.以下说法正确的是( )| A. | 细杆cd一定向下做匀速直线运动 | |
| B. | 细杆cd可能向下做匀加速直线运动 | |
| C. | 拉力F做的功等于回路中产生的焦耳热 | |
| D. | 拉力F做的功等于回路中产生的焦耳热与细杆ab克服擦力做的功之和 |
| A. | 汽车做匀加速直线运动,自行车做匀速直线运动 | |
| B. | 自行车经过6s追上汽车 | |
| C. | 在t=2.5 s时,自行车和汽车相距最远,最远距离为12m | |
| D. | 自行车经过6.2s追上汽车 |
| A. | 重力的平均功率相同 | B. | 落地时重力的瞬时功率相同 | ||
| C. | 重力的平均功率不同 | D. | 落地时重力的瞬时功率不同 |
 如图所示,以MN为边界分布着范围足够大的等大反向的匀强磁场,一个质量为m,带电量为-q的粒子,以初速度v0从边界上的P点沿与MN成30°角的方向射入MN右侧磁场区域后,通过了边界上的Q点,已知PQ间距为L.(不计粒子重力)
如图所示,以MN为边界分布着范围足够大的等大反向的匀强磁场,一个质量为m,带电量为-q的粒子,以初速度v0从边界上的P点沿与MN成30°角的方向射入MN右侧磁场区域后,通过了边界上的Q点,已知PQ间距为L.(不计粒子重力)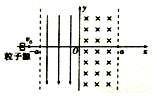 如图,在-a≤x≤0区域内存在与y轴平行的匀强电场,在0≤x≤a区域内存在与xy平面垂直的匀强磁场,电场、磁场方向如图所示.粒子源位于x坐标轴上,在xy平面内发射出大量同种带正电粒子,所有粒子的初速度方向均沿x轴正方向.不计粒子重力.
如图,在-a≤x≤0区域内存在与y轴平行的匀强电场,在0≤x≤a区域内存在与xy平面垂直的匀强磁场,电场、磁场方向如图所示.粒子源位于x坐标轴上,在xy平面内发射出大量同种带正电粒子,所有粒子的初速度方向均沿x轴正方向.不计粒子重力. 如图所示,光滑水平面右端B处连接一个竖直的半径为R的光滑半径固定轨道,在离B距离为x的A点,用水平恒力将质量为m的质点从静止开始推到B处后撤去恒力,质点恰好能通过半圆轨道的C点,则水平恒力大小为$\frac{5mgR}{2x}$.
如图所示,光滑水平面右端B处连接一个竖直的半径为R的光滑半径固定轨道,在离B距离为x的A点,用水平恒力将质量为m的质点从静止开始推到B处后撤去恒力,质点恰好能通过半圆轨道的C点,则水平恒力大小为$\frac{5mgR}{2x}$.