题目内容
12.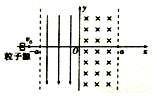 如图,在-a≤x≤0区域内存在与y轴平行的匀强电场,在0≤x≤a区域内存在与xy平面垂直的匀强磁场,电场、磁场方向如图所示.粒子源位于x坐标轴上,在xy平面内发射出大量同种带正电粒子,所有粒子的初速度方向均沿x轴正方向.不计粒子重力.
如图,在-a≤x≤0区域内存在与y轴平行的匀强电场,在0≤x≤a区域内存在与xy平面垂直的匀强磁场,电场、磁场方向如图所示.粒子源位于x坐标轴上,在xy平面内发射出大量同种带正电粒子,所有粒子的初速度方向均沿x轴正方向.不计粒子重力.(1)若带电粒子先后穿越电场、磁场后,速度方向仍与x轴平行,求带电粒子的初速度v0与电场强度E、磁感应强度B三者之间的关系;
(2)相关物理量取值如下:电场强度E=36V/m,带电粒子的初速度v0=18m/s、电荷量q=1×10-2C、质量m=3×10-4kg,a=0.36m.通过调整磁感应强度B的大小,能否使带电粒子到达坐标原点O?(sin37°=0.6、cos37°=0.8)
分析 (1)粒子在电场中做类平抛运动,进入磁场做匀速圆周运动,作出轨迹图,根据牛顿第二定律和运动学公式求出粒子进入磁场时的速度,结合半径公式求出带电粒子的初速度v0与电场强度E、磁感应强度B三者之间的关系.
(2)作出轨迹图,根据牛顿第二定律和运动学公式得出类平抛运动下降的高度和速度与竖直方向的夹角,结合几何关系判断能否使带电粒子到达坐标原点O.
解答 解:(1)带电粒子进入y轴左侧的匀强电场后做类平抛运动:a=v0t,${v_y}=\frac{qE}{m}t$,
设粒子进入磁场时的速度为v,与y轴负方向的夹角为θ,有:$v=\frac{v_y}{cosθ}$,
带电粒子在y轴右侧的匀强磁场中做匀速圆周运动:$qvB=m\frac{v^2}{R}$,
带电粒子穿越磁场后速度方向与x轴平行,如图所示:
根据几何关系:Rcosθ=a,
联立解得:${v_0}=\frac{E}{B}$.
(2)带电粒子在y轴左侧做类平抛运动:a=v0t
$h=\frac{1}{2}\frac{qE}{m}{t^2}$,
${v_y}=\frac{qE}{m}t$,
$tanθ=\frac{v_0}{v_y}$,
代入数据解得:h=0.24m,θ=37°.
粒子在y轴右侧的匀强磁场中做匀速圆周运动,设刚好打到O点时,几何关系如图:
h=2Rsinθ.
代入数据解得:R=0.20m.
圆周轨迹最右端与y轴的距离:d=Rcosθ+R=0.36m=a,
带电粒子刚好能在磁场中完成圆周运动,能使带电粒子到达坐标原点O.
答:(1)带电粒子的初速度v0与电场强度E、磁感应强度B三者之间的关系为${v_0}=\frac{E}{B}$.
(2)能使带电粒子到达坐标原点O.
点评 本题考查带电粒子在复合场中的运动,掌握处理类平抛运动的方法,对应粒子在磁场中的运动,解题的关键在于确定圆心和半径,结合半径公式或周期公式进行求解.

 如图所示,竖直放置的长为2L的轻杆上端及正中央固定两个质量均为m、可视为质点的小球,下端固定在铰链上,杆从静止开始自由倒下,不计一切摩擦及空气阻力,则A着地时的速度为( )
如图所示,竖直放置的长为2L的轻杆上端及正中央固定两个质量均为m、可视为质点的小球,下端固定在铰链上,杆从静止开始自由倒下,不计一切摩擦及空气阻力,则A着地时的速度为( )| A. | $\frac{1}{5}$$\sqrt{15gL}$ | B. | $\frac{2}{5}$$\sqrt{15gL}$ | C. | $\frac{1}{5}$$\sqrt{30gL}$ | D. | $\frac{2}{5}$$\sqrt{30gL}$ |
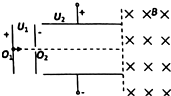 如图所示,加速电场电压为U1,偏转电场电压为U2,B为右侧足够大的有左边界匀强磁场,一束由${\;}_{1}^{1}$H、${\;}_{1}^{2}$H组成的粒子流在O1处静止开始经U1加速,再经U2偏转后进入右侧匀强磁场,且均能从左边界离开磁场.不计粒子间相互作用,则下列说法正确的是( )
如图所示,加速电场电压为U1,偏转电场电压为U2,B为右侧足够大的有左边界匀强磁场,一束由${\;}_{1}^{1}$H、${\;}_{1}^{2}$H组成的粒子流在O1处静止开始经U1加速,再经U2偏转后进入右侧匀强磁场,且均能从左边界离开磁场.不计粒子间相互作用,则下列说法正确的是( )| A. | 两种粒子在电场中会分为两束 | |
| B. | 两种粒子在磁场中会分为两束 | |
| C. | 两种粒子进磁场位置和出磁场位置间的距离比为1:$\sqrt{2}$ | |
| D. | 两种粒子进磁场位置和出磁场位置间的距离都与U2无关 |
| A. | 0.2m/s | B. | 0.02m/s | C. | 0.5m/s | D. | 0.05m/s |
| A. | 同步卫星处于平衡状态 | B. | 同步卫星的周期大于24小时 | ||
| C. | 同步卫星距地面的高度是一定的 | D. | 同步卫星的速度是不变的 |
 如图所示,螺旋形光滑轨道竖直放置,P、Q为对应的轨道最高点,一个小球以一定速度沿轨道切线方向进入轨道,且能过轨道最高点P,则下列说法正确的是( )
如图所示,螺旋形光滑轨道竖直放置,P、Q为对应的轨道最高点,一个小球以一定速度沿轨道切线方向进入轨道,且能过轨道最高点P,则下列说法正确的是( )| A. | 轨道对小球不做功,小球通过P点的角速度小于通过Q点的角速度 | |
| B. | 轨道对小球不做功,小球通过P点的线速度小于通过Q点的线速度 | |
| C. | 小球通过P点时的向心加速度大于通过Q点时的向心加速度 | |
| D. | 小球通过P点时对轨道的压力大于通过Q点时对轨道的压力 |
 如图,分界线的上方是垂直纸面向里的无限大的匀强磁场,磁感应强度为B;下方是水平方向的无限大匀强电场,场强为E,质量为m的带电粒子分别带等量异种电荷,电荷量都是q,它们同时从A点以垂直于分界线的速度v飞入磁场,并且最终在电场中的某点相遇,不计重力、两个点电荷之间的作用力和一切阻力,求:
如图,分界线的上方是垂直纸面向里的无限大的匀强磁场,磁感应强度为B;下方是水平方向的无限大匀强电场,场强为E,质量为m的带电粒子分别带等量异种电荷,电荷量都是q,它们同时从A点以垂直于分界线的速度v飞入磁场,并且最终在电场中的某点相遇,不计重力、两个点电荷之间的作用力和一切阻力,求: 按照我国月球探测活动计划,共分两步.第一步“绕月”工程,圆满完成任务后,再开展第二步“落月”工程.假设月球半径为R,月球表面的重力加速度为g0,飞船沿距月球中心距离为3R的圆形轨道Ⅰ运动,到达轨道的A点,点火变轨进入椭圆轨道Ⅱ,到达轨道Ⅱ的近月点B再次点火进入近月轨道Ⅲ(B点离月球表面的高度小于月球的半径)绕月球做圆周运动,根据以上信息,求(1)飞船在轨道I上运行的速度大小;
按照我国月球探测活动计划,共分两步.第一步“绕月”工程,圆满完成任务后,再开展第二步“落月”工程.假设月球半径为R,月球表面的重力加速度为g0,飞船沿距月球中心距离为3R的圆形轨道Ⅰ运动,到达轨道的A点,点火变轨进入椭圆轨道Ⅱ,到达轨道Ⅱ的近月点B再次点火进入近月轨道Ⅲ(B点离月球表面的高度小于月球的半径)绕月球做圆周运动,根据以上信息,求(1)飞船在轨道I上运行的速度大小;