题目内容
12. 中国航天局在2015年年底发射了高分四号卫星,这是中国首颗地球同步轨道高分辨率对地观测卫星,如图所示,A是静止在赤道上随地球自转的物体,B、C是同在赤道平面内的两颗人造卫星,B位于离地高度等于地球半径的圆形轨道上,C是高分四号卫星.则下列判断正确的是( )
中国航天局在2015年年底发射了高分四号卫星,这是中国首颗地球同步轨道高分辨率对地观测卫星,如图所示,A是静止在赤道上随地球自转的物体,B、C是同在赤道平面内的两颗人造卫星,B位于离地高度等于地球半径的圆形轨道上,C是高分四号卫星.则下列判断正确的是( )| A. | 物体A随地球自转的角速度大于卫星B的角速度 | |
| B. | 卫星B的线速度小于卫星C的线速度 | |
| C. | 物体A随地球自转的周期大于卫星C的周期 | |
| D. | 物体A随地球自转的向心加速度小于卫星C的向心加速度 |
分析 A、C的角速度、周期相等,根据万有引力提供向心力得出线速度、角速度、向心加速度与轨道半径的关系,从而比较大小.
解答 解:A、A、C的角速度相等,根据$G\frac{Mm}{{r}^{2}}=mr{ω}^{2}$得:$ω=\sqrt{\frac{GM}{{r}^{3}}}$,C的轨道半径大于B的轨道半径,则C的角速度小于B的角速度,可知物体A随地球自转的角速度小于卫星B的角速度,故A错误.
B、根据$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}$得:v=$\sqrt{\frac{GM}{r}}$,B的轨道半径小于C的轨道半径,则B的线速度大于C的线速度,故B错误.
C、物体A随地球自转的周期等于卫星C的周期,故C错误.
D、A、C的角速度相等,根据a=rω2知,物体A随地球自转的向心加速度小于C的向心加速度,故D正确.
故选:D.
点评 解决本题的关键知道卫星做圆周运动向心力的来源,结合牛顿第二定律分析判断,注意A做圆周运动向心力不是靠万有引力提供向心力.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
3. 一质点在斜面上做直线运动,某段过程中其速度的平方和位移的图象如图所示,图中a、b和c均为已知,重力加速度为g,由图可知( )
一质点在斜面上做直线运动,某段过程中其速度的平方和位移的图象如图所示,图中a、b和c均为已知,重力加速度为g,由图可知( )
 一质点在斜面上做直线运动,某段过程中其速度的平方和位移的图象如图所示,图中a、b和c均为已知,重力加速度为g,由图可知( )
一质点在斜面上做直线运动,某段过程中其速度的平方和位移的图象如图所示,图中a、b和c均为已知,重力加速度为g,由图可知( )| A. | 该过程中上滑所用时间与下滑所用时间相等 | |
| B. | 斜面与水平面夹角的正弦值为$\frac{a+b}{4gc}$ | |
| C. | 上滑过程机械能的变化量大于下滑过程中机械能的变化量 | |
| D. | 图线①表示质点沿斜面下滑过程,图线②表示质点沿斜面上滑过程 |
7. 有一种杂技表演叫“飞车走壁”,由杂技演员驾驶摩托车沿光滑圆台形表演台的侧壁高速行驶,在水平面内做匀速圆周运动.图中粗线圆表示摩托车的行驶轨迹,轨迹离地面的高度为h.如果增大高度h,则下列关于摩托车说法正确的是( )
有一种杂技表演叫“飞车走壁”,由杂技演员驾驶摩托车沿光滑圆台形表演台的侧壁高速行驶,在水平面内做匀速圆周运动.图中粗线圆表示摩托车的行驶轨迹,轨迹离地面的高度为h.如果增大高度h,则下列关于摩托车说法正确的是( )
 有一种杂技表演叫“飞车走壁”,由杂技演员驾驶摩托车沿光滑圆台形表演台的侧壁高速行驶,在水平面内做匀速圆周运动.图中粗线圆表示摩托车的行驶轨迹,轨迹离地面的高度为h.如果增大高度h,则下列关于摩托车说法正确的是( )
有一种杂技表演叫“飞车走壁”,由杂技演员驾驶摩托车沿光滑圆台形表演台的侧壁高速行驶,在水平面内做匀速圆周运动.图中粗线圆表示摩托车的行驶轨迹,轨迹离地面的高度为h.如果增大高度h,则下列关于摩托车说法正确的是( )| A. | 对侧壁的压力N增大 | B. | 做圆周运动的周期T不变 | ||
| C. | 做圆周运动的线速度增大 | D. | 做圆周运动的向心力F增大 |
2. 如图所示,两光滑平行导轨水平放置在匀强磁场中,磁场垂直于导轨所在平面向里,金属棒ab可沿导轨自由滑动,导轨一端跨接一个定值电阻R,导轨及金属棒的电阻均不计,现将金属棒沿导轨由静止向右拉.若保持拉力F恒定,当速度为v时,加速度为a1,最终以速度2v做匀速运动;若保持拉力的功率P恒定,当速度为v时,加速度为a2,最终也以2v做匀速运动,则以下关系正确的是( )
如图所示,两光滑平行导轨水平放置在匀强磁场中,磁场垂直于导轨所在平面向里,金属棒ab可沿导轨自由滑动,导轨一端跨接一个定值电阻R,导轨及金属棒的电阻均不计,现将金属棒沿导轨由静止向右拉.若保持拉力F恒定,当速度为v时,加速度为a1,最终以速度2v做匀速运动;若保持拉力的功率P恒定,当速度为v时,加速度为a2,最终也以2v做匀速运动,则以下关系正确的是( )
 如图所示,两光滑平行导轨水平放置在匀强磁场中,磁场垂直于导轨所在平面向里,金属棒ab可沿导轨自由滑动,导轨一端跨接一个定值电阻R,导轨及金属棒的电阻均不计,现将金属棒沿导轨由静止向右拉.若保持拉力F恒定,当速度为v时,加速度为a1,最终以速度2v做匀速运动;若保持拉力的功率P恒定,当速度为v时,加速度为a2,最终也以2v做匀速运动,则以下关系正确的是( )
如图所示,两光滑平行导轨水平放置在匀强磁场中,磁场垂直于导轨所在平面向里,金属棒ab可沿导轨自由滑动,导轨一端跨接一个定值电阻R,导轨及金属棒的电阻均不计,现将金属棒沿导轨由静止向右拉.若保持拉力F恒定,当速度为v时,加速度为a1,最终以速度2v做匀速运动;若保持拉力的功率P恒定,当速度为v时,加速度为a2,最终也以2v做匀速运动,则以下关系正确的是( )| A. | a1=3a2 | B. | a2=3a1 | C. | P=FV | D. | P=2FV |
6. 如图所示,两方向相反,磁感应强度大小均为B的匀强磁场被边长为L的等边三角形ABC边界分开,三角形内磁场方向垂直纸面向里,三角形顶点A处由一质子源,能沿∠BAC的角平分线发射速度不同的质子(质子重力不计),所有质子均能通过C点,质子比荷$\frac{q}{m}=\frac{1}{k}$,则质子的速度可能为( )
如图所示,两方向相反,磁感应强度大小均为B的匀强磁场被边长为L的等边三角形ABC边界分开,三角形内磁场方向垂直纸面向里,三角形顶点A处由一质子源,能沿∠BAC的角平分线发射速度不同的质子(质子重力不计),所有质子均能通过C点,质子比荷$\frac{q}{m}=\frac{1}{k}$,则质子的速度可能为( )
 如图所示,两方向相反,磁感应强度大小均为B的匀强磁场被边长为L的等边三角形ABC边界分开,三角形内磁场方向垂直纸面向里,三角形顶点A处由一质子源,能沿∠BAC的角平分线发射速度不同的质子(质子重力不计),所有质子均能通过C点,质子比荷$\frac{q}{m}=\frac{1}{k}$,则质子的速度可能为( )
如图所示,两方向相反,磁感应强度大小均为B的匀强磁场被边长为L的等边三角形ABC边界分开,三角形内磁场方向垂直纸面向里,三角形顶点A处由一质子源,能沿∠BAC的角平分线发射速度不同的质子(质子重力不计),所有质子均能通过C点,质子比荷$\frac{q}{m}=\frac{1}{k}$,则质子的速度可能为( )| A. | $\frac{BL}{k}$ | B. | $\frac{BL}{2k}$ | C. | $\frac{2BL}{3k}$ | D. | $\frac{BL}{8k}$ |

 如图所示,光滑的轻杆可以绕其一端O,在竖直面内做匀速圆周运动,杆上穿着两个质量均为m=1kg的小球(小球均视为质点,杆与小球之间无摩擦力).小球A与转轴O之间的距离为L=0.3m,小球A与小球B之间距离也为L,长为L的轻绳一端连接小球A另一端连接在O点,小球A和小球B也用长为L的轻绳连接(图中未画出轻绳),两根轻绳能承受的最大张力相同,均为Tmax=110N.(g=10m/s2)
如图所示,光滑的轻杆可以绕其一端O,在竖直面内做匀速圆周运动,杆上穿着两个质量均为m=1kg的小球(小球均视为质点,杆与小球之间无摩擦力).小球A与转轴O之间的距离为L=0.3m,小球A与小球B之间距离也为L,长为L的轻绳一端连接小球A另一端连接在O点,小球A和小球B也用长为L的轻绳连接(图中未画出轻绳),两根轻绳能承受的最大张力相同,均为Tmax=110N.(g=10m/s2)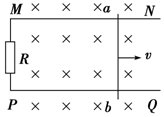 如图所示,两根光滑足够长的平行金属导轨MN和PQ水平放置,间距为l=0.4m,其右端接入一个阻值R=4Ω的定值电阻,金属轨道的电阻忽略不计.将此框架放在水平面上,空间有垂直轨道平面的匀强磁场,磁感应强度为B=1T,一个内阻r=1Ω的金属杆在力F的作用下以5m/s的速度在轨道上向右匀速运动,求:
如图所示,两根光滑足够长的平行金属导轨MN和PQ水平放置,间距为l=0.4m,其右端接入一个阻值R=4Ω的定值电阻,金属轨道的电阻忽略不计.将此框架放在水平面上,空间有垂直轨道平面的匀强磁场,磁感应强度为B=1T,一个内阻r=1Ω的金属杆在力F的作用下以5m/s的速度在轨道上向右匀速运动,求: