��Ŀ����
1��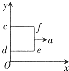 �ھ�Ե�⻬��ˮƽ���Ϸ���һ����Ϊm���߳�ΪL���������߿�cdef���߿���ܵ���ΪR��xOy��һ�����ڸ�ˮƽ���ڵ�ƽ��ֱ������ϵ���߿����ڿռ�����ŷ���ֱ��xOyƽ��Ĵų���������Ϊ��x��y�����ų��ĴŸ�Ӧǿ�ȴ�СΪB=B0+kx��ʽ��B0��k��Ϊ������t=0ʱ�̣��߿��cd��λ��x=0�����߿��ھ�ֹ����ͼ��ʾ����t=0ʱ�̿�ʼ�����߿�ʩһ��x���������������ʹ�߿��Լ��ٶ�a�������ȼ����˶���������t=t0ʱ�̣�
�ھ�Ե�⻬��ˮƽ���Ϸ���һ����Ϊm���߳�ΪL���������߿�cdef���߿���ܵ���ΪR��xOy��һ�����ڸ�ˮƽ���ڵ�ƽ��ֱ������ϵ���߿����ڿռ�����ŷ���ֱ��xOyƽ��Ĵų���������Ϊ��x��y�����ų��ĴŸ�Ӧǿ�ȴ�СΪB=B0+kx��ʽ��B0��k��Ϊ������t=0ʱ�̣��߿��cd��λ��x=0�����߿��ھ�ֹ����ͼ��ʾ����t=0ʱ�̿�ʼ�����߿�ʩһ��x���������������ʹ�߿��Լ��ٶ�a�������ȼ����˶���������t=t0ʱ�̣���1���߿�����ĸ�Ӧ�綯�ƵĴ�С��
��2����x���������ˮƽ�����Ĵ�С��
���� ��1���߿����ȼ����˶������˶�ѧ��ʽ���t0ʱ���ڵ�λ�ƣ����ɷ����ڵ�Ÿ�Ӧ�������Ӧ�綯�ƣ�
��2���ɱպϵ�·ŷķ���������Ӧ��������F=BIL����߿����ܵİ������������ţ�ٵڶ�������ˮƽ�����Ĵ�С��
��� �⣺��1���߿����ȼ����˶���t0ʱ���ڵ�λ��Ϊ��x=$\frac{1}{2}a{t}_{0}^{2}$
t0ʱ���߿���ٶ�Ϊ��v=at0
cd�߲����ĸ�Ӧ�綯�ƴ�СΪ��E1=��B0+kx��Lv
fe�߲����ĸ�Ӧ�綯�ƴ�СΪ��E2=[B0+k��x+L��]Lv
��·�ܵĸ�Ӧ�綯��Ϊ��E=E2-E1=kL2vx=$\frac{1}{2}k{L}^{2}va{t}_{0}^{2}$
��2���߿��и�Ӧ����Ϊ��I=$\frac{E}{R}$
cd�����ܵİ�������СΪ��F1=��B0+kx��IL����������
fe�����ܵİ�������СΪ��F2=[B0+k��x+L��]IL����������
�����߿����ܵİ�����ΪFA=F2-F1=kIL2����������
����ţ�ٵڶ����ɵã�F-FA=ma
�������ˮƽ����Ϊ��F=ma+$\frac{{k}^{2}{L}^{4}va{t}_{0}^{2}}{2R}$
�𣺣�1���߿�����ĸ�Ӧ�綯�ƵĴ�С��$\frac{1}{2}k{L}^{2}va{t}_{0}^{2}$��
��2����x���������ˮƽ�����Ĵ�С��ma+$\frac{{k}^{2}{L}^{4}va{t}_{0}^{2}}{2R}$��
���� ����Ҫ���շ����ڵ�Ÿ�Ӧ���ɡ��պϵ�·ŷķ���ɺͰ������Ĺ�ʽ���ؼ�Ҫע��cd�ߺ�fe�߶�Ҫ������Ӧ�綯�ƣ����ڷ��綯�ƣ����߶�Ҫ�ܵ��������������������෴��֪�����ٶ����߿����ܵĺ��������ȣ�

 һ����������ϵ�д�
һ����������ϵ�д�| A�� | ����ͨ��������ȹ����������С������ | |
| B�� | �������������Ĺ�����������ʱ������� | |
| C�� | �������ڣ����ɵľ���ϵ���뵯���쳤�������� | |
| D�� | ������������������������ĵ��Ʋ������ |

 ��ͼ��ʾ��ʵ��װ�ã�������̽�����Ծ�ֹ�����������������ٶȵĹ�ϵ��
��ͼ��ʾ��ʵ��װ�ã�������̽�����Ծ�ֹ�����������������ٶȵĹ�ϵ��
 ��ͼ��ʾ����ֱ���õ�����ܴ��ƽ�д��������a��b���Ϊd��a��b��ĵ糡ǿ��ΪE������һ�������Һ�δ�a���±�Ե������a�壩�Գ��ٶ�v0��ֱ��������糡�������ɵ�b��ʱ���ٶȴ�С��Ϊv0���������Ϊˮƽ���ҸպôӸ߶�ҲΪd�����촩��b���ϵ�С������ǿ�ų������ų��ĴŸ�Ӧǿ�ȴ�СΪB=$\frac{E}{{v}_{0}}$������ֱֽ������ų�����Ŀ���ΪL���������ٶ�Ϊg��
��ͼ��ʾ����ֱ���õ�����ܴ��ƽ�д��������a��b���Ϊd��a��b��ĵ糡ǿ��ΪE������һ�������Һ�δ�a���±�Ե������a�壩�Գ��ٶ�v0��ֱ��������糡�������ɵ�b��ʱ���ٶȴ�С��Ϊv0���������Ϊˮƽ���ҸպôӸ߶�ҲΪd�����촩��b���ϵ�С������ǿ�ų������ų��ĴŸ�Ӧǿ�ȴ�СΪB=$\frac{E}{{v}_{0}}$������ֱֽ������ų�����Ŀ���ΪL���������ٶ�Ϊg��

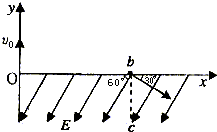 ��ͼ��ʾ��һ����Ϊm��������Ϊ+q���������ٶ�v0��O����y������������Ÿ�Ӧǿ��ΪB��Բ����ǿ�ų����ų�����ֱֽ�����⣬���ӷɳ��ų�����ӵ�b������x�ᣬ�ٶȷ�����x��������ļн�Ϊ30�㣬ͬʱ���볡ǿΪE��������x�Ḻ�����60���б���µ���ǿ�糡�У���ͨ����b�����·���c�㣬�����������ƣ�����
��ͼ��ʾ��һ����Ϊm��������Ϊ+q���������ٶ�v0��O����y������������Ÿ�Ӧǿ��ΪB��Բ����ǿ�ų����ų�����ֱֽ�����⣬���ӷɳ��ų�����ӵ�b������x�ᣬ�ٶȷ�����x��������ļн�Ϊ30�㣬ͬʱ���볡ǿΪE��������x�Ḻ�����60���б���µ���ǿ�糡�У���ͨ����b�����·���c�㣬�����������ƣ�����