题目内容
19. 如图甲所示,离子发生器能连续均匀地发射质量为m.电荷量为+q的离子.并从O点无初速进入间距为d1的两平行极板AB之间.离子穿过极板B上的小孔后,恰好沿两平行板MN间的中心线射入偏转电场.已知MN两板长均为L,MN两板间所加电压恒为U,且M板的电势高于N板电势.则:
如图甲所示,离子发生器能连续均匀地发射质量为m.电荷量为+q的离子.并从O点无初速进入间距为d1的两平行极板AB之间.离子穿过极板B上的小孔后,恰好沿两平行板MN间的中心线射入偏转电场.已知MN两板长均为L,MN两板间所加电压恒为U,且M板的电势高于N板电势.则:(1)若UAB=U1(U1为定值)求离子射入偏转电场时的速度为多大;
(2)若UAB=U1.离子恰能从极板N的中心小孔P处飞出.求MN两饭间的距离d;
(3)若极板AB间所加电压随时间变化的规律如图乙所示.已知电压的变化周期T=$\sqrt{\frac{128{d}_{1}^{2}m}{9q{U}_{1}}}$.求能从小孔P处飞的离子数目与发射总数的比值.
分析 (1)粒子在加速电场中,电场力做功,由动能定理求出速度v0.
(2)粒子进入偏转电场后,做类平抛运动,运用运动的合成与分解求出MN两饭间的距离d;
(3)求出粒子一直做加速运动穿过AB的时间,然后判断出能到达P的粒子的数目与发射总数的比值.
解答 解:(1)由动能定理可得:$q{U}_{1}=\frac{1}{2}m{{v}_{0}}^{2}$
解得:${v}_{0}=\sqrt{\frac{2q{U}_{1}}{m}}$
(2)粒子进入偏转电场后做类平抛运动,竖直方向:$y=\frac{d}{2}=\frac{1}{2}a{t}^{2}$
其中:$a=\frac{qU}{md}$
在偏转电场中,水平方向:$\frac{1}{2}$L=v0t
由以上三式可得:d=$\frac{qU}{md}•\frac{Lm}{2q{U}_{1}}$=$\frac{U{L}^{2}}{2d{U}_{1}}$
即:d=$L•\sqrt{\frac{U}{2{U}_{1}}}$
(3)由题意可知,只有在AB中一直做匀加速直线运动的粒子才能恰好到达P点,粒子穿过AB的时间t,则:
t=$\frac{{d}_{1}}{\frac{{v}_{0}}{2}}=\sqrt{\frac{2m{d}_{1}^{2}}{q{U}_{1}}}$
可知,只有在$\frac{T}{2}-t$前发射的粒子才能到达P点,其余的粒子不能到达P点,所以能从小孔P处飞的离子数目与发射总数的比值:
$\frac{{n}_{P}}{N}=\frac{\frac{T}{2}-t}{T}$
代入数据解得:$\frac{{n}_{P}}{N}=\frac{1}{8}$
答:(1)若UAB=U1(U1为定值)求离子射入偏转电场时的速度为$\sqrt{\frac{2q{U}_{1}}{m}}$;
(2)若UAB=U1.离子恰能从极板N的中心小孔P处飞出.MN两饭间的距离d为$L•\sqrt{\frac{U}{2{U}_{1}}}$;
(3)若极板AB间所加电压随时间变化的规律如图乙所示.已知电压的变化周期T=$\sqrt{\frac{128{d}_{1}^{2}m}{9q{U}_{1}}}$.能从小孔P处飞的离子数目与发射总数的比值是$\frac{1}{8}$.
点评 本题关键是明确粒子的受力特点和运动规律,然后结合动能定理、类似平抛运动的分运动公式和几何关系列式求解.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案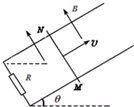 如图所示,两条足够长的光滑平行金属导轨与水平面的夹角为θ,下端接有定值电阻R,匀强磁场垂直于导轨平面向上,磁感应强度为B.现给导体棒MN一平行于导轨的初速度v,使导体棒保持与导轨垂直并沿导轨向上运动,经过一段时间导体棒又回到原位置.不计导轨和导体棒的电阻,在这一过程中,下列说法正确的是( )
如图所示,两条足够长的光滑平行金属导轨与水平面的夹角为θ,下端接有定值电阻R,匀强磁场垂直于导轨平面向上,磁感应强度为B.现给导体棒MN一平行于导轨的初速度v,使导体棒保持与导轨垂直并沿导轨向上运动,经过一段时间导体棒又回到原位置.不计导轨和导体棒的电阻,在这一过程中,下列说法正确的是( )| A. | 导体棒上滑时棒中的电流方向由N到M | |
| B. | 导体棒上滑阶段和下滑阶段的同一位置受到的安培力大小相同 | |
| C. | 整个过程中流过导体某一横截面上的电荷量必然为零 | |
| D. | 导体棒在上升阶段动能减小量等于回路中热能的增加量 |
| A. | 三个离子离开偏转电场时的速度方向相同 | |
| B. | 三个离子在偏转电场中的位移相等 | |
| C. | 一价的氢离子、一价的氦离子离开电场时的动能相等 | |
| D. | 三个离子同时离开偏转电场 |
| A. | 电子离开加速电场时的速度为$\sqrt{\frac{e{U}_{1}}{m}}$ | |
| B. | 电子飞越偏转电场的时间为$\sqrt{\frac{m{L}^{2}}{2{U}_{1}}}$ | |
| C. | 电子飞越偏转电场过程中,动能增量为$\frac{e{{U}_{2}}^{2}{L}^{2}}{4{d}^{2}{U}_{1}}$ | |
| D. | 电子飞越偏转电场过程中,动量的增量为U2L$\sqrt{\frac{me}{2{U}_{1}{d}^{2}}}$ |
 某学习小组在“研究匀变速直线运动”的实验中,用如图5所示的气垫导轨装置来测滑块的加速度,由导轨标尺可以测出两个光电门之间的距离L,窄遮光板的宽度为d,窄遮光板依次通过两个光电门的时间分别为t1、t2.
某学习小组在“研究匀变速直线运动”的实验中,用如图5所示的气垫导轨装置来测滑块的加速度,由导轨标尺可以测出两个光电门之间的距离L,窄遮光板的宽度为d,窄遮光板依次通过两个光电门的时间分别为t1、t2.
 如图所示,开有小孔的平行板水平放置,两极板接在电压大小可调的电源上,用喷雾器将油滴喷注在小孔上方.已知两极板间距为d,油滴密度为ρ,电子电量为e,重力加速度为g,油滴视为球体,油滴运动时所受空气的粘滞阻力大小Ff=6πηrv(r为油滴半径、η为粘滞系数,且均为已知),油滴所带电量是电子电量的整数倍,喷出的油滴均相同,不考虑油滴间的相互作用.
如图所示,开有小孔的平行板水平放置,两极板接在电压大小可调的电源上,用喷雾器将油滴喷注在小孔上方.已知两极板间距为d,油滴密度为ρ,电子电量为e,重力加速度为g,油滴视为球体,油滴运动时所受空气的粘滞阻力大小Ff=6πηrv(r为油滴半径、η为粘滞系数,且均为已知),油滴所带电量是电子电量的整数倍,喷出的油滴均相同,不考虑油滴间的相互作用.