题目内容
8.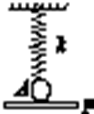 如图所示,劲度系数为k的轻弹簧下端系一个质量为m的小球A,小球被水平挡板P托住使弹簧长度恰为自然长度(小球与挡板不粘连),然后使挡板P以恒定的加速度a(a<g)开始竖直向下做匀加速直线运动,则( )
如图所示,劲度系数为k的轻弹簧下端系一个质量为m的小球A,小球被水平挡板P托住使弹簧长度恰为自然长度(小球与挡板不粘连),然后使挡板P以恒定的加速度a(a<g)开始竖直向下做匀加速直线运动,则( )| A. | 小球与与挡板分离的时间为t=$\sqrt{\frac{ka}{2m(g-a)}}$ | |
| B. | 小球与与挡板分离的时间为t=$\sqrt{\frac{2m(g-a)}{ka}}$ | |
| C. | 小球从开始运动直到最低点的过程中,小球速度最大时弹簧的伸长量x=$\frac{mg}{k}$ | |
| D. | 小球从开始运动直到最低点的过程中,小球速度最大时弹簧的伸长量x=$\frac{m(g-a)}{k}$ |
分析 在物体与托盘脱离前,物体受重力、弹簧拉力和托盘支持力的作用,随着托盘向下运动,弹簧的弹力增大,托盘支持力减小,但仍维持合外力不变,加速度不变,物体随托盘一起向下匀加速运动.当托盘运动至使支持力减小为零后,弹簧拉力的增大将使物体的加速度开始小于a,物体与托盘脱离,此时支持力N=0,对物体分析,根据牛顿第二定律求出弹簧的形变量,结合位移时间公式求出脱离的时间.
解答 解:小球与挡板之间弹力为零时分离,此时小球的加速度仍为a,
由牛顿第二定律得:mg-kx=ma,
由匀变速直线运动的位移公式得:x=$\frac{1}{2}$at2,
解得:t=$\sqrt{\frac{2m(g-a)}{ka}}$;
小球速度最大时合力为零,x=$\frac{mg}{k}$;
故选:BC.
点评 解决本题的关键知道物体与托盘脱离的条件,即N=0,结合牛顿第二定律和运动学公式综合求解.

练习册系列答案
相关题目
3. 如图所示,一车载导航仪放在底边水平的三角形支架上,处于静止状态.稍微减小支架的倾斜角度,以下说法正确的是( )
如图所示,一车载导航仪放在底边水平的三角形支架上,处于静止状态.稍微减小支架的倾斜角度,以下说法正确的是( )
 如图所示,一车载导航仪放在底边水平的三角形支架上,处于静止状态.稍微减小支架的倾斜角度,以下说法正确的是( )
如图所示,一车载导航仪放在底边水平的三角形支架上,处于静止状态.稍微减小支架的倾斜角度,以下说法正确的是( )| A. | 导航仪所受弹力变小 | B. | 导航仪所受摩擦力变小 | ||
| C. | 支架施加给导航仪的作用力变小 | D. | 支架施加给导航仪的作用力变大 |
18. 如图所示,在光滑小滑轮C正下方相距h的A处固定一电量为Q的点电荷,电量为q的带电小球B,用绝缘细线拴着,细线跨过定滑轮,另一端用适当大小的力拉住,使小球处于静止状态,这时小球与A点的距离为R,细线CB与AB垂直.(静电力恒量为K,环境可视为真空),若小球所受的重力的为G,缓慢拉动细线(始终保持小球平衡)直到小球刚到滑轮的正下方过程中,拉力所做的功为W1,电场力做功为W2,则下列关系式正确的是( )
如图所示,在光滑小滑轮C正下方相距h的A处固定一电量为Q的点电荷,电量为q的带电小球B,用绝缘细线拴着,细线跨过定滑轮,另一端用适当大小的力拉住,使小球处于静止状态,这时小球与A点的距离为R,细线CB与AB垂直.(静电力恒量为K,环境可视为真空),若小球所受的重力的为G,缓慢拉动细线(始终保持小球平衡)直到小球刚到滑轮的正下方过程中,拉力所做的功为W1,电场力做功为W2,则下列关系式正确的是( )
 如图所示,在光滑小滑轮C正下方相距h的A处固定一电量为Q的点电荷,电量为q的带电小球B,用绝缘细线拴着,细线跨过定滑轮,另一端用适当大小的力拉住,使小球处于静止状态,这时小球与A点的距离为R,细线CB与AB垂直.(静电力恒量为K,环境可视为真空),若小球所受的重力的为G,缓慢拉动细线(始终保持小球平衡)直到小球刚到滑轮的正下方过程中,拉力所做的功为W1,电场力做功为W2,则下列关系式正确的是( )
如图所示,在光滑小滑轮C正下方相距h的A处固定一电量为Q的点电荷,电量为q的带电小球B,用绝缘细线拴着,细线跨过定滑轮,另一端用适当大小的力拉住,使小球处于静止状态,这时小球与A点的距离为R,细线CB与AB垂直.(静电力恒量为K,环境可视为真空),若小球所受的重力的为G,缓慢拉动细线(始终保持小球平衡)直到小球刚到滑轮的正下方过程中,拉力所做的功为W1,电场力做功为W2,则下列关系式正确的是( )| A. | W1=$\frac{mg}{2h}$(h2-R2) | B. | W2=GR(1-$\frac{R}{h}$) | C. | W1=$\frac{hKQq}{{R}^{2}}$(1-$\frac{R}{h}$) | D. | G=$\frac{khQq}{{R}^{2}}$ |
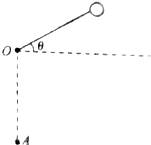 如图所示,摆球的质量为m,从偏离水平方向θ=30°的位置由静止释放,求:
如图所示,摆球的质量为m,从偏离水平方向θ=30°的位置由静止释放,求: 如图,在场强大小为E、水平向右的匀强电场中,一轻杆可绕固定转轴O在竖直平面内自由转动.杆的两端分别固定两电荷量均为q的小球A、B,A带正电,B带负电;A、B两球到转轴O的距离分别为2l、l,所受重力大小均为电场力大小的$\sqrt{3}$倍.开始时杆与电场间夹角为θ(90°≤θ≤180°).将杆从初始位置由静止释放,以O点为重力势能和电势能零点.求:
如图,在场强大小为E、水平向右的匀强电场中,一轻杆可绕固定转轴O在竖直平面内自由转动.杆的两端分别固定两电荷量均为q的小球A、B,A带正电,B带负电;A、B两球到转轴O的距离分别为2l、l,所受重力大小均为电场力大小的$\sqrt{3}$倍.开始时杆与电场间夹角为θ(90°≤θ≤180°).将杆从初始位置由静止释放,以O点为重力势能和电势能零点.求: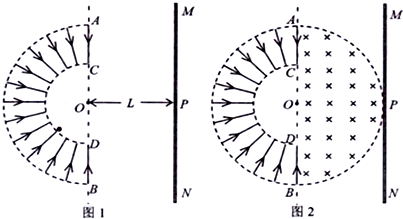
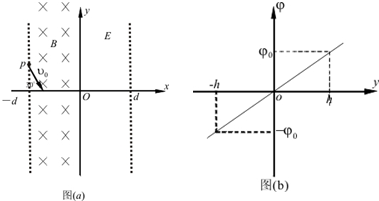
 如图所示,在直角坐标系O-xyz中存在磁感应强度为B=$\frac{2m}{q}$$\sqrt{\frac{g}{h}}$,方向竖直向下的匀强磁场,在(0,0,h)处固定一电量为+q(q>0)的点电荷,在xOy平面内有一质量为m,电量为-q的微粒绕原点O沿图示方向作匀速圆周运动.若该微粒的圆周运动可以等效为环形电流,求此等效环形电流强度I.(重力加速度为g)
如图所示,在直角坐标系O-xyz中存在磁感应强度为B=$\frac{2m}{q}$$\sqrt{\frac{g}{h}}$,方向竖直向下的匀强磁场,在(0,0,h)处固定一电量为+q(q>0)的点电荷,在xOy平面内有一质量为m,电量为-q的微粒绕原点O沿图示方向作匀速圆周运动.若该微粒的圆周运动可以等效为环形电流,求此等效环形电流强度I.(重力加速度为g) 如图所示为汽车电磁感应减速带原理图(俯视图),在汽车通过的区域设置匀强磁场,其方向垂直地面向上,大小为B,宽度为d.在汽车底部固定有一个长度L1、宽度L2的N匝矩形线圈,线圈的总电阻为R,车和线圈的总质量为m,假设汽车运动过程中所受阻力恒为f.当汽车以初速度v0进入磁场区域的左侧,开始以大小为a的恒定加速度减速驶入磁场区域,线圈全部进入磁场后,立即做匀速直线运动,直至完全离开缓冲区域,已知从线圈刚进入磁场到完全穿出磁场的过程中,汽车的牵引力做的总功为W.从线圈的前边与磁场左边线重合开始计时.求:
如图所示为汽车电磁感应减速带原理图(俯视图),在汽车通过的区域设置匀强磁场,其方向垂直地面向上,大小为B,宽度为d.在汽车底部固定有一个长度L1、宽度L2的N匝矩形线圈,线圈的总电阻为R,车和线圈的总质量为m,假设汽车运动过程中所受阻力恒为f.当汽车以初速度v0进入磁场区域的左侧,开始以大小为a的恒定加速度减速驶入磁场区域,线圈全部进入磁场后,立即做匀速直线运动,直至完全离开缓冲区域,已知从线圈刚进入磁场到完全穿出磁场的过程中,汽车的牵引力做的总功为W.从线圈的前边与磁场左边线重合开始计时.求: