题目内容
13.如图(a)所示,在-d≤x≤0范围内存在垂直于纸面向里的匀强磁场,在0≤x≤d范围内存在着电场(电场方向图中未画出).一质量为m,电荷量为q的正电粒子,在磁场x=-d边界上的P点以速度大小为v0,方向与磁场边界的夹角为30°垂直于磁场方向射入.随后粒子经坐标原点O沿+x方向射入电场区域(粒子重力不计).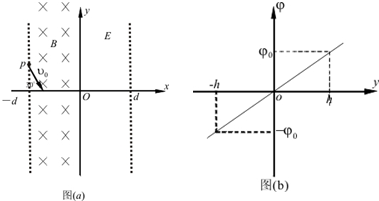
(1)求匀强磁场的磁感应强度B;
(2)若在0≤x≤d的区域的坐标平面内只加平行于y轴的电场,电场中的各点电势φ随坐标y分布如图(b)所示(图中的φ0、h为已知量),求粒子从x=d边界飞出电场时的位置坐标;
(3)若在0≤x≤d的区域再加上平行于x轴方向的匀强电场E1,使经坐标原点O沿+x方向射入的带电粒子能越过y轴回到匀强磁场,求匀强电场场强的最小值E1.
分析 (1)粒子在磁场中做匀速圆周运动,画出轨迹,求轨迹半径,由牛顿第二定律求磁感应强度B.
(2)根据电势高低可知所加的电场为匀强电场,方向y轴的负方向,场强为E=$\frac{{φ}_{0}}{h}$.带电粒子在电场中做类似于平抛运动,根据牛顿第二定律求加速度,由分位移公式求解即可.
(3)粒子在电场中沿x轴方向的分运动是沿+x方向做匀减速直线运动,至分速度为零后反向做匀加速直线运动,根据牛顿第二定律和速度位移关系公式结合求解.
解答  解:(1)粒子在磁场中做匀速圆周运动,设其运动的半径为r,有:Bqv0=$\frac{{v}_{0}^{2}}{r}$ …①
解:(1)粒子在磁场中做匀速圆周运动,设其运动的半径为r,有:Bqv0=$\frac{{v}_{0}^{2}}{r}$ …①
由几何关系有:r=$\frac{d}{cos30°}$ …②
得:B=$\frac{\sqrt{3}m{v}_{0}}{2qd}$ …③
(2)所加的电场为匀强电场,方向y轴的负方向,场强为E,则:E=$\frac{{φ}_{0}}{h}$ …④
带电粒子在电场中做类似于平抛运动,有:
d=v0t …⑤
y=$\frac{1}{2}a{t}^{2}$ …⑥
a=$\frac{qE}{m}$ …⑦
联立④⑤⑥⑦式得:y=$\frac{q{φ}_{0}{d}^{2}}{2hm{v}_{0}^{2}}$
粒子飞出电场时的位置坐标为(d,-$\frac{q{φ}_{0}{d}^{2}}{2hm{v}_{0}^{2}}$)
(3)粒子在电场中沿x轴方向的分运动是沿+x方向做匀减速直线运动,至分速度为零后反向做匀加速直线运动,对应匀强电场场强的最小值E1有:
E1q=ma1…⑧
${v}_{0}^{2}$=2a1d…⑨
联立⑧⑨两式得:E1=$\frac{m{v}_{0}^{2}}{2qd}$…⑩
答:(1)匀强磁场的磁感应强度B为$\frac{\sqrt{3}m{v}_{0}}{2qd}$;
(2)粒子飞出电场时的位置坐标为(d,-$\frac{q{φ}_{0}{d}^{2}}{2hm{v}_{0}^{2}}$)
(3)匀强电场场强的最小值E1为$\frac{m{v}_{0}^{2}}{2qd}$.
点评 带电粒子在组合场中的运动问题,首先要运用动力学方法分析清楚粒子的运动情况,再选择合适方法处理.对于匀变速曲线运动,常常运用运动的分解法,将其分解为两个直线的合成,由牛顿第二定律和运动学公式结合求解;对于磁场中圆周运动,要正确画出轨迹,由几何知识求解半径.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案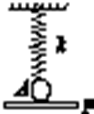 如图所示,劲度系数为k的轻弹簧下端系一个质量为m的小球A,小球被水平挡板P托住使弹簧长度恰为自然长度(小球与挡板不粘连),然后使挡板P以恒定的加速度a(a<g)开始竖直向下做匀加速直线运动,则( )
如图所示,劲度系数为k的轻弹簧下端系一个质量为m的小球A,小球被水平挡板P托住使弹簧长度恰为自然长度(小球与挡板不粘连),然后使挡板P以恒定的加速度a(a<g)开始竖直向下做匀加速直线运动,则( )| A. | 小球与与挡板分离的时间为t=$\sqrt{\frac{ka}{2m(g-a)}}$ | |
| B. | 小球与与挡板分离的时间为t=$\sqrt{\frac{2m(g-a)}{ka}}$ | |
| C. | 小球从开始运动直到最低点的过程中,小球速度最大时弹簧的伸长量x=$\frac{mg}{k}$ | |
| D. | 小球从开始运动直到最低点的过程中,小球速度最大时弹簧的伸长量x=$\frac{m(g-a)}{k}$ |
 某研究性学习小组利用伏安法测定某一电池组的电动势和内阻,实验原理如图所示,其中,虚线框内为用灵敏电流计G改装的电流表A,V为标准电压表,E为待测电池组,S为开关,R为滑动变阻器,R0是标称值为4.0Ω的定值电阻.
某研究性学习小组利用伏安法测定某一电池组的电动势和内阻,实验原理如图所示,其中,虚线框内为用灵敏电流计G改装的电流表A,V为标准电压表,E为待测电池组,S为开关,R为滑动变阻器,R0是标称值为4.0Ω的定值电阻.①已知灵敏电流计G的满偏电流Ig=100μA、内阻rg=2.0kΩ,若要改装后的电流表满偏电流为200mA,应并联一只1.0Ω(保留2位有效数字)的定值电阻R1.
②某次实验的数据如表所示:该小组借鉴“研究匀变速直线运动”实验中计算加速度的方法(逐差法),计算出电池组的内阻r=1.66Ω(保留3位有效数字).
| 测量次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 电压表V读数U/V | 5.26 | 5.16 | 5.04 | 4.94 | 4.83 | 4.71 | 4.59 | 4.46 |
| 改装表A读数I/mA | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
A.电压表内阻的影响 B.滑动变阻器的最大阻值偏小
C.R1的实际阻值比计算值偏小 D.R0的实际阻值比标称值偏大.
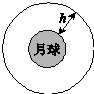 我国已相继完成“神十”与“天宫”对接、“嫦娥”携“玉兔”落月两大航天工程.某航天爱好者提出“玉兔”回家的设想:如图所示,将携带“玉兔”的返回系统由月球表面发射到h高度的轨道上,与在该轨道绕月球做圆周运动的飞船对接,然后由飞船送“玉兔”返回地球.设“玉兔”质量为m,月球半径为R,月面的重力加速度为g月.以月面为零势能面,“玉兔”在h高度的引力势能可表示为Ep=$\frac{GMmh}{R(R+h)}$,其中G为引力常量,M为月球质量.若忽略月球的自转,从开始发射到对接完成需要对“玉兔”做的功为( )
我国已相继完成“神十”与“天宫”对接、“嫦娥”携“玉兔”落月两大航天工程.某航天爱好者提出“玉兔”回家的设想:如图所示,将携带“玉兔”的返回系统由月球表面发射到h高度的轨道上,与在该轨道绕月球做圆周运动的飞船对接,然后由飞船送“玉兔”返回地球.设“玉兔”质量为m,月球半径为R,月面的重力加速度为g月.以月面为零势能面,“玉兔”在h高度的引力势能可表示为Ep=$\frac{GMmh}{R(R+h)}$,其中G为引力常量,M为月球质量.若忽略月球的自转,从开始发射到对接完成需要对“玉兔”做的功为( )| A. | $\frac{m{g}_{月}R}{R+h}$(h+2R) | B. | $\frac{m{g}_{月}R}{R+h}$(h+$\sqrt{2}$R) | C. | $\frac{m{g}_{月}R}{R+h}$(h+$\frac{\sqrt{2}}{2}$R) | D. | $\frac{m{g}_{月}R}{R+h}$(h+$\frac{1}{2}$R) |
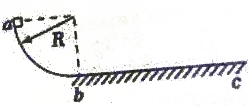 如图所示,质量为m的物块在光滑的$\frac{1}{4}$圆弧轨道的顶端a点由静止开始下滑,圆弧轨道半径为R,最低点b与粗糙水平轨道想接,物块最终滑至c点停止,bc间距为S,求:
如图所示,质量为m的物块在光滑的$\frac{1}{4}$圆弧轨道的顶端a点由静止开始下滑,圆弧轨道半径为R,最低点b与粗糙水平轨道想接,物块最终滑至c点停止,bc间距为S,求: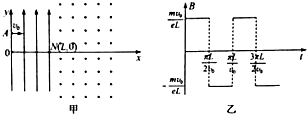
 一质量为m、电荷量为q的带正电粒子(重力不计),以初速度v0进入电势差为U的带窄缝的平行板电极S1和S2间的电场,经电场加速后,沿OX方向进入磁感应强度为B、方向垂直纸面向外的有界匀强磁场,OX垂直平板电极S2.当粒子从p点离开磁场时,其速度方向与OX方向的夹角θ=60°,整个装置处于真空中,如图所示.求:
一质量为m、电荷量为q的带正电粒子(重力不计),以初速度v0进入电势差为U的带窄缝的平行板电极S1和S2间的电场,经电场加速后,沿OX方向进入磁感应强度为B、方向垂直纸面向外的有界匀强磁场,OX垂直平板电极S2.当粒子从p点离开磁场时,其速度方向与OX方向的夹角θ=60°,整个装置处于真空中,如图所示.求: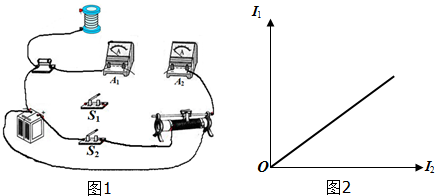
 在地面附近的真空中,存在着竖直向上的匀强电场和垂直电场方向水平向里的匀强磁场,如图甲所示.磁场的磁感应强度B(图象中的B0末知)随时间t的变化情况如图乙所示.该区域中有一条水平直线MN,D是MN上的一点.在t=0时刻,有一个质量为m、电荷量为+q的小球(可看做质点),从M点开始沿着水平直线以速度v0向右做匀速直线运动,t0时刻恰好到达N点.经观测发现,小球在t=2t0至t=3t0时间内的某一时刻,又竖直向下经过直线MN上的D点,并且以后小球多次水平向右或竖直向下经过D点.不考虑地磁场的影响,求:
在地面附近的真空中,存在着竖直向上的匀强电场和垂直电场方向水平向里的匀强磁场,如图甲所示.磁场的磁感应强度B(图象中的B0末知)随时间t的变化情况如图乙所示.该区域中有一条水平直线MN,D是MN上的一点.在t=0时刻,有一个质量为m、电荷量为+q的小球(可看做质点),从M点开始沿着水平直线以速度v0向右做匀速直线运动,t0时刻恰好到达N点.经观测发现,小球在t=2t0至t=3t0时间内的某一时刻,又竖直向下经过直线MN上的D点,并且以后小球多次水平向右或竖直向下经过D点.不考虑地磁场的影响,求: