题目内容
18. 如图所示,有一质量为m的小球和一静置于光滑水平面上的质量为2m的滑块,滑块左侧是一光滑圆弧轨道.小球以速度v0滑上圆弧轨道,已知小球在上升过程中始终未能冲出圆弧轨道,重力加速度为g,求:
如图所示,有一质量为m的小球和一静置于光滑水平面上的质量为2m的滑块,滑块左侧是一光滑圆弧轨道.小球以速度v0滑上圆弧轨道,已知小球在上升过程中始终未能冲出圆弧轨道,重力加速度为g,求:(1)小球在圆弧轨道上能上升的最大高度(用v0、g表示);
(2)小球离开圆弧轨道时的速度大小.
分析 (1)小球和轨道组成的系统,在水平方向上不受外力,水平方向动量守恒.当小球在圆弧轨道上到达最高点时小球与轨道的速度相同.规定小球运动的初速度方向为正方向,根据动量守恒列式,再根据机械能守恒列式,联立方程即可求解;
(2)小球从轨道左端离开滑块时,根据动量守恒和机械能守恒定律列式,联立方程即可求解.
解答 解:(1)小球和圆弧轨道在水平方向上动量守恒.
当小球在圆弧轨道上到达最高点时小球与轨道的速度相同,
设共同速度为v.规定小球运动的初速度方向为正方向,
根据动量守恒定律有:mv0=(m+2m)v,解得:v=$\frac{{v}_{0}}{3}$,
根据机械能守恒得:$\frac{1}{2}$mv02=$\frac{1}{2}$(m+2m)v2+mgh,解得:h=$\frac{{v}_{0}^{2}}{3g}$;
(2)小球从轨道左端离开滑块时,以向右为正方向,
由动量守恒定律得:mv0=mv1+2mv2,
根据机械能守恒得:$\frac{1}{2}$mv02=$\frac{1}{2}$mv12+$\frac{1}{2}$•2mv22,
联立可得:v1=-$\frac{1}{3}$v0,则小球离开圆弧轨道时的速度大小为$\frac{1}{3}$v0.
答:(1)小球在圆弧轨道上能上升的最大高度为$\frac{{v}_{0}^{2}}{3g}$;
(2)小球离开圆弧轨道时的速度大小为$\frac{1}{3}$v0.
点评 本题关键要判断出系统水平方向的动量守恒,要注意系统的总动量并不守恒.对于光滑的情形,要考虑机械能守恒定律.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
9.如图所示,水平传送带的长度L=5m,皮带轮的半径R=0.1m,皮带轮以角速度ω顺时针匀速转动,现有一小物体(视为质点)以水平速度v0从A点滑上传送带,越过B点后做平抛运动,其水平位移为x.保持物体的初速度v0不变,多次改变皮带轮的角速度ω,依次测量水平位移x,得到如图所示的x-ω图象,则下列说法正确的是( )


| A. | 当0<ω<10rad/s时,物体在AB之间做匀减速直线运动 | |
| B. | 当ω≥30rad/s时,物体在AB之间做匀速直线运动 | |
| C. | B端距地面的高度h=5m | |
| D. | 物体水平初速度为v0=5m/s |
13.在地球(看作质量均匀分布的球体)上空有许多同步卫星,关于这些同步卫星下面说法中正确的是( )
| A. | 它们的质量可能不同 | B. | 它们的速率可能不同 | ||
| C. | 它们的角速度可能不同 | D. | 它们离地心的距离可能不同 |
3. 如图电路所示,当ab两端接入50V电压时,cd两端为10V;当cd两端接入50V电压时,ab两端电压为25V,则R1:R2:R3之比是( )
如图电路所示,当ab两端接入50V电压时,cd两端为10V;当cd两端接入50V电压时,ab两端电压为25V,则R1:R2:R3之比是( )
 如图电路所示,当ab两端接入50V电压时,cd两端为10V;当cd两端接入50V电压时,ab两端电压为25V,则R1:R2:R3之比是( )
如图电路所示,当ab两端接入50V电压时,cd两端为10V;当cd两端接入50V电压时,ab两端电压为25V,则R1:R2:R3之比是( )| A. | 4:2:1 | B. | 2:1:1 | C. | 3:2:1 | D. | 以上都不对 |
20.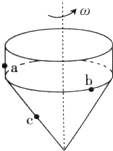 如图为一个玩具陀螺,a、b和c是陀螺上的三个点,当陀螺绕垂直于地面的轴线以角速度ω稳定旋转时,下列表述正确的是( )
如图为一个玩具陀螺,a、b和c是陀螺上的三个点,当陀螺绕垂直于地面的轴线以角速度ω稳定旋转时,下列表述正确的是( )
 如图为一个玩具陀螺,a、b和c是陀螺上的三个点,当陀螺绕垂直于地面的轴线以角速度ω稳定旋转时,下列表述正确的是( )
如图为一个玩具陀螺,a、b和c是陀螺上的三个点,当陀螺绕垂直于地面的轴线以角速度ω稳定旋转时,下列表述正确的是( )| A. | a、b和c三点的角速度大小相等 | B. | a、b和c三点的线速度大小相等 | ||
| C. | a、b和c三点的向心加速度大小相等 | D. | c的周期比a、b的大 |
 两根光滑的长直金属导轨平行置于同一水平面内,导轨间距为L,电阻不计.M、P处接有如图所示电路,电路中各电阻的阻值均为R,电容器的电容为C.长度也为L、阻值同为R的金属棒ab垂直于导轨放置,导轨处于磁感强度为B、方向竖直向下的匀强磁场中,ab在外力的作用下向右匀速运动且与导轨保持良好接触,在ab运动距离s的过程中,整个回路中产生的焦耳热为Q.求:
两根光滑的长直金属导轨平行置于同一水平面内,导轨间距为L,电阻不计.M、P处接有如图所示电路,电路中各电阻的阻值均为R,电容器的电容为C.长度也为L、阻值同为R的金属棒ab垂直于导轨放置,导轨处于磁感强度为B、方向竖直向下的匀强磁场中,ab在外力的作用下向右匀速运动且与导轨保持良好接触,在ab运动距离s的过程中,整个回路中产生的焦耳热为Q.求: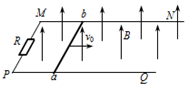 如图所示,水平面上有两根足够长的光滑平行金属导轨MN和PQ,两导轨间距为L,电阻均可忽略不计,在M和P之间接有阻值为R的定值电阻.导体杆ab质量为m,电阻为r,并与导轨接触良好.整个装置处于方向竖直向上、磁感应强度为B的匀强磁场中.现给ab杆大小为v0的初速度,使杆向右运动.求:
如图所示,水平面上有两根足够长的光滑平行金属导轨MN和PQ,两导轨间距为L,电阻均可忽略不计,在M和P之间接有阻值为R的定值电阻.导体杆ab质量为m,电阻为r,并与导轨接触良好.整个装置处于方向竖直向上、磁感应强度为B的匀强磁场中.现给ab杆大小为v0的初速度,使杆向右运动.求: 图1为用打点计时器验证机械能守恒定律的实验装置.实验中得到一条点迹清晰的纸带如图2所示.打P点时,重物的速度为零;A、B、C为3个连续点,测得各点与P的距离如图所示.已知电源频率为50Hz,当地的重力加速度g=9.8m/s2,重物质量为0.2kg,则:
图1为用打点计时器验证机械能守恒定律的实验装置.实验中得到一条点迹清晰的纸带如图2所示.打P点时,重物的速度为零;A、B、C为3个连续点,测得各点与P的距离如图所示.已知电源频率为50Hz,当地的重力加速度g=9.8m/s2,重物质量为0.2kg,则: