题目内容
5.一物体从某一点以初速度v出发,做匀减速直线运动,经过时间t速度恰好减为零,且刚好到达终点,则物体经t0(t0<t)时刻距终点的距离为( )| A. | $\frac{vt}{2}$ | B. | vt0(1-$\frac{{t}_{0}}{2t}$) | C. | $\frac{vt_0^2}{2t}$ | D. | $\frac{{v{{(t-{t_0})}^2}}}{2t}$ |
分析 物体做匀减速直线运动,由平均速度求出t时间内物体的位移,由加速度的定义式求出加速度,再由位移时间公式求解t0时间内的位移,即可得到物体经t0时刻距终点的距离.
解答 解:物体在t时间内通过的位移 x=$\frac{v+0}{2}t$=$\frac{v}{2}t$
加速度为 a=$\frac{0-v}{t}$=-$\frac{v}{t}$
则t0时间内的位移 x0=vt0+$\frac{1}{2}a{t}_{0}^{2}$
物体经t0时刻距终点的距离为 S=x-x0.
联立解得 S=$\frac{v(t-{t}_{0})^{2}}{2t}$
故选:D.
点评 匀变速直线运动的公式较多,要根据题设条件灵活选择公式求解.公式x=$\frac{{v}_{0}+v}{2}t$的特点是不涉及加速度.本题也可以运用逆向思维解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13. 倾角为θ的斜面,长为l,在顶端水平抛出一个小球,小球刚好落在斜面的底端,如图所示,那么小球的初速度v0的大小是( )
倾角为θ的斜面,长为l,在顶端水平抛出一个小球,小球刚好落在斜面的底端,如图所示,那么小球的初速度v0的大小是( )
 倾角为θ的斜面,长为l,在顶端水平抛出一个小球,小球刚好落在斜面的底端,如图所示,那么小球的初速度v0的大小是( )
倾角为θ的斜面,长为l,在顶端水平抛出一个小球,小球刚好落在斜面的底端,如图所示,那么小球的初速度v0的大小是( )| A. | cosθ$\sqrt{\frac{gl}{2sinθ}}$ | B. | cosθ$\sqrt{\frac{gl}{sinθ}}$ | C. | sinθ$\sqrt{\frac{gl}{2cosθ}}$ | D. | sinθ$\sqrt{\frac{gl}{cosθ}}$ |
17.如图所示,当氢原子从n=4迁到n=2的能级和从n=3迁到n=1的能级时,分别辐射出光子a和光子b,则( )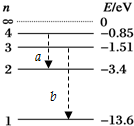

| A. | 由于放出光子,原子的能量增加 | |
| B. | 光子a的能量小于光子b的能量 | |
| C. | 光子a的频率大于光子b的频率 | |
| D. | 若光子a能使某金属发生光电效应,则光子b不一定能使该金属发生光电效应 |
15.一个人以相同速率从同一高度按不同方向推出铅球,从推出到铅球落地( )
| A. | 重力的冲量相同 | B. | 落地时铅球动量相同 | ||
| C. | 此过程重力功相同 | D. | 落地时铅球动能相同 |
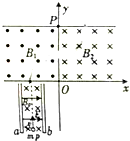 如图所示,纸面内有直角坐标系xOy,在第一,二象限y≤p的区域内分别存在垂直于纸面的匀强磁场B1,B2,方向相反,在第三象限有一速度选择器,a,b板与x轴垂直,板间匀强电场E和匀强磁场B0相互垂直,现有一质量为m,电荷量大小为q的粒子能够沿直线通过速度选择器,并垂直于x轴射入磁场B1,并最终从第一象限y=p上的某点垂直射出磁场B2,已知粒子始终在纸面内运动,且每次均垂直越过y轴进入磁场,不计粒子重力.
如图所示,纸面内有直角坐标系xOy,在第一,二象限y≤p的区域内分别存在垂直于纸面的匀强磁场B1,B2,方向相反,在第三象限有一速度选择器,a,b板与x轴垂直,板间匀强电场E和匀强磁场B0相互垂直,现有一质量为m,电荷量大小为q的粒子能够沿直线通过速度选择器,并垂直于x轴射入磁场B1,并最终从第一象限y=p上的某点垂直射出磁场B2,已知粒子始终在纸面内运动,且每次均垂直越过y轴进入磁场,不计粒子重力.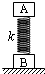 如图所示,A、B两个物块用轻弹簧相连接,它们的质量分别为mA=2kg和mB=3kg,弹簧的劲度系数为k=400N/m,物块B置于水平地面上,物块A靠弹簧托住,系统处于静止状态.现用一恒力F=60N竖直向上拉物块A使之向上运动,重力加速度g取10m/s2,试求:
如图所示,A、B两个物块用轻弹簧相连接,它们的质量分别为mA=2kg和mB=3kg,弹簧的劲度系数为k=400N/m,物块B置于水平地面上,物块A靠弹簧托住,系统处于静止状态.现用一恒力F=60N竖直向上拉物块A使之向上运动,重力加速度g取10m/s2,试求: